Персистентное дерево отрезков это

Персистентное дерево отрезков

Общий подход к персистентности почти любой ссылочной структуры — это создавать копии всех вершин, в которых хоть что-то меняется, и менять это что-то в копиях, никогда не изменяя уже существующие вершины.

Персистентное дерево отрезков здесь не исключение. Просто будем при спуске создавать копию вершины перед тем, как что-либо менять в ней самой или её потомках. Асимптотика операций от этого не изменится, разве что общее потребление памяти увеличится до $O(m \log n)$.

Удобнее всего по аналогии с push в отложенных операциях определить функцию copy , копирующую детей текущей вершины, и просто без разбору вызывать её во всех вершинах, в которых что-то может измениться.

 Теперь осталось только создать список версий, и после каждой операции копировать туда новый корень:

В качестве альтернативного подхода можно копировать не детей, а текущую вершину, и возвращать её из рекурсии и переподвешивать за родителя. Это вычислительно эффективнее, но нужно сильно изменить реализацию.

#Применения

В контексте задач на структуры данных персистентное дерево отрезков особенно часто применяют в задачах, где применили бы метод сканирующей прямой, если бы запросы были известны заранее.

#Сумма на прямоугольнике

Задача. Даны $n$ точек на плоскости. Нужно в онлайн ответить на $q$ запросов числа точек на прямоугольнике.

Если бы можно было отвечать в оффлайн, мы бы разбили запрос на два запроса на префиксах и прошлись бы сканлайном слева направо, добавляя $y$-координаты точек в дерево отрезков и отвечая на запросы суммы на подотрезках — но так делать мы не можем.

Но точки в оффлайн известны. Добавим их в таком же порядке в персистентное дерево отрезков, а не обычное, и сохраним корни деревьев с разными $x$-координатами в порядке увеличения.

Теперь мы можем ответить на запрос, так же декомпозировав его на два и перенаправив их в две разные версии дерева отрезков, соответствующие большей и меньшей $x$-координатам. Таким образом, можно отвечать на запросы в онлайн за $O(q \log n)$ времени и памяти.

#Порядковые статистики

Задача. Дан отрезок из $n$ целых чисел и $q$ запросов $k$-той порядковой статистики на подотрезке.

Во-первых, сожмем все числа, чтобы они были от 1 до $n$.

Затем, пройдёмся с персистентным деревом отрезков для суммы по массиву слева направо, и когда будем обрабатывать элемент $a_k$, добавим единицу к $a_k$-ому элементу в дереве отрезков. Заметим, что сумма с $l$ по $r$ в таком дереве будет равна количеству элементов между $l$ и $r$ на текущем префиксе.

Дальше определим разность деревьев как дерево отрезков, которое получилось бы, если бы оно было построено поверх разности соответствующих массивов.

Что будет находиться в разности $r$-го и $l$-го дерева ($r > l$)? Там будут находиться количества вхождений чисел на отрезке массива с $l$ по $r$ — какой-то массив целых неотрицательных чисел. Если в таком разностном дереве сделать спуск, который находит последнюю позицию, у которой сумма на префиксе не превышает $k$ — она и будет ответом на запрос.

Если не обязательно строить разностное дерево явно, чтобы делать по нему спуск — можно просто спускаться одновременно в двух деревьях и везде вместо суммы $s$ использовать $(s_r — s_l)$:

Отметим, что эту и предыдущую задачу также можно решить через mergesort tree за $O(n \log^2 n)$, а также двумерными структурами за такую же асимптотику.

#Доминирующий элемент

Задача. Дан массив из $n$ элементов. Требуется ответить на $m$ запросов, есть ли на отрезке $[l, r)$ доминирующий элемент — тот, который встречается на нём хотя бы $\frac$ раз.

У этой задачи есть удивительно простое решение — взять около 100 случайных элементов для каждого проверить, является ли он доминирующим. Проверку можно выполнять за $O(\log n)$, посчитав для каждого значения отсортированный список позиций, на которых он встречается, и сделав в нём два бинпоиска. Вероятность ошибки в худшем случае равна $\frac>$, и ей на практике можно пренебречь.

Но проверять 100 сэмплов — долго. Построим такое же дерево отрезков, как в прошлой задаче, и решим задачу «найти число, большее $\frac$ в массиве из $n$ неотрицательных целых чисел с суммой не более $n$» относительно разностного дерева. Это тоже будет спуском по нему: каждый раз идём в того сына, где сумма больше (потому что сын с меньшей суммой точно не доминирующий). Если в листе, куда мы пришли, значение больше нужного, возвращаем true , иначе false .

Упражнение. Придумайте, как модифицировать спуск в задаче где доминирующим считается элемент, встречающийся хотя бы $\frac$ раз для маленького $k$ (от 2 до 5).

#Как персистентный массив

С помощью дерева отрезков обычно и реализуют полностью персистентный массив — в общем случае быстрее $O(\log n)$ на запрос не получается. Персистентный массив в свою очередь можно использовать, чтобы делать персистентными не-ссылочные структуры — например, систему непересекающихся множеств.

В СНМ мы храним всё состояние в массивах, которые можно просто сделать персистентными через дерево отрезков. Асимптотика такой структуры будет $O(n \log n)$ времени и памяти — причем логарифм здесь и от самого СНМа (нужно пройтись по $O(\log n)$ предков — эвристику сжатия путей мы использовать не можем), так и от персистентного ДО (обновить значение какого-то $p_v$ и $s_v$ / $h_v$).

Источник

Персистентные деревья отрезков

Структуры данных можно разделить на две группы: эфемерные (ephemeral) и персистентные (persistent).

Эфемерными называются структуры данных, хранящие только последнюю свою версию.
Персистентные структуры, то есть те, которые сохраняют все свои предыдущие версии, в свою очередь можно разделить еще на две подгруппы: если структура данных, позволяет изменять только последнюю версию, она называется частично персистентной (partially persistent), если же позволяется изменять любую версию, такая структура считается полностью персистентной (fully persistent).

Далее будет рассмотрено дерево отрезков и его полностью персистентная версия.
Весь код доступен на GitHub.

Дерево отрезков

Те, кто уже знаком с деревьями отрезков, могут сразу перейти к разделу о персистентной версии.

Деревом отрезков называется структура данных, позволяющая для данного массива A быстро выполнять следующие операции:

Описание

Пусть n — длина массива A , будем заполнять его нейтральными элементами до тех пор, пока его длина не станет равна степени двойки (например, если f — сумма, массив будет дополняться нулями).

Теперь построим такое двоичное дерево, что его листьями будут все элементы A и глубина всех листьев одинакова, а во всех остальных вершинах будут храниться значения f от значений дочерних вершин.

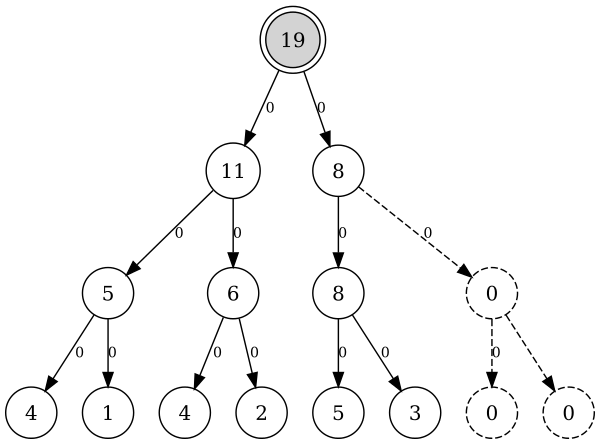
Рассмотрим в качестве примера дерево отрезков для массива A = [4, 1, 4, 2, 5, 3] :

Хранить такое дерево удобно как и двоичную кучу: в виде массива вершин, записанных подряд сверху вниз слева направо:

19 11 8 5 6 8 0 4 1 4 2 5 3 0 0

В таком случае для вершины с индексом i ее предком будет вершина ((i — 1) / 2) , а левый и правый дочерние вершины будут иметь индексы (2 * i + 1) и (2 * i + 2) соответственно (считая, что элементы в массиве нумеруются с нуля).

Построение

Удобно строить дерево отрезков рекурсивно сверху вниз: для каждой вершины построить левую и правую дочерние вершины, после чего посчитать значение f от их значений, а для листов же просто записать соответствующее значение массива в дерево.

Строя дерево таким образом каждая вершина будет посещена один раз, и, так как количество вершин в дереве Θ(n), сложность построения также Θ(n).

Изменение

После того, как было изменено значение какого-либо элемента, в дереве могли испортиться некоторые из значений предков данного элемента. Исправить это можно, пересчитав значения предков данного элемента, поднимаясь по дереву снизу вверх.

Например, если в массиве A заменить A[3] на 10 , то будут пересчитаны вершины со значениями 6 , 11 и 19 .

Так как высота дерева log n, то операция изменения затронет ровно log n вершин, значит, асимптотика операции O(log n).

Вычисление F

Данная операция будет выполняться рекурсивно сверху вниз.

Пусть в произвольной вершине v посчитано F для диапазона l..r , тогда нетрудно проверить, что в левой дочерней вершине посчитано значение F для l..((l + r) / 2) , а в правой — для ((l + r) / 2 + 1)..r .

Предположим, что поступил запрос F(i, j) , и текущая вершина — v . Возможны два случая:

• В узле v уже посчитано значение F(i, j) . Тогда ответом на полученный запрос будет значение вершины v .
• В узле v записано F для большего диапазона. В таком случае рекурсивно вызовем вычисление F(i, (l + r) / 2) для левого дочерней вершины и F((l + r) / 2 + 1, j) для правой, и ответом будет f от этих двух значений.

Пример

Персистентное дерево отрезков

Добиться персистентности можно разными способами, самый простой из них — при каждом изменении делать полную копию старой версии и изменять ее, как обычное дерево отрезков, однако такой способ слишком затратен по памяти и ухудшает асимптотику операции Change до O(n).

Построение

Построение персистентного дерева отрезков будет аналогично построению обычного дерева отрезков за исключением того, что теперь для каждой вершины дополнительно придется в явном виде хранить ссылки на дочерние вершины.
Также дополнительно понадобится хранить массив вершин, являющихся корнями в соответствующих версиях дерева. При построении в него добавляется единственная вершина, являющаяся корнем полученного дерева.

Так как единственное изменение по сравнению с эфемерным деревом отрезков — это добавление информации о левой и правой дочерних вершинах, сложность построения осталось неизменной, то есть Θ(n).

Изменение

Вместо полного копирования дерева при изменении вершины к нему будут добавлены только те вершины, которые должны были измениться, и вместо изменения значений старых вершин, пересчитанные значения будут сохранены в новые. Все новые вершины будут ссылаться на одну вершину из дерева старой версии и на одну из только что добавленных.

Добавление новой ветки делается аналогично построению всего дерева за исключением того, что вместо построения двух дочерних вершин, новая вершина строится только в том направлении, в котором лежит измененная вершина.
После этого обновляется массив корневых вершин.

Так как при изменении только добавляется log n вершин, асимптотика операции — O(log n).

Вычисление F

Вычисление F производится аналогично эфемерному дереву. Единственные отличия: переходы к дочерним вершинам и запуск из разных корневых вершин.
Отсюда следует сложность O(log n).

Пример

Задачи

При помощи персистентного дерева отрезков можно решить задачу «Откат» (разбор задачи). Решение задачи с использованием приведенной выше реализации персистентного дерева отрезков доступно на GitHub.
Также здесь можно прочитать обсуждение задачи о k-ой порядковой статистике на диапазоне.

Источник