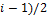Пирамидальная сортировка (бинарные деревья)
Сортировка – один из наиболее сложных и важных для изучения алгоритмов.
Во-первых, сортировка – это общая задача многих компьютерных приложений. Практически любой список ценнее, когда он отсортирован по какому-либо определенному принципу.
Во-вторых, многие алгоритмы сортировки являются интересными примерами программирования, демонстрирующих важные методы: частное упорядочивание, рекурсия, объединение списков, сохранение двоичных деревьев в массивах.
У каждого алгоритма сортировки есть свои преимущества и недостатки. Производительность различных алгоритмов зависит от типа данных, начального расположения, размера и значений. Важно выбрать тот алгоритм, который лучше всего подходит для решения конкретной задачи.
Сортировка – одна из немногих задач с точными теоретическими границами производительности. Любой алгоритм сортировки, который использует сравнения, занимает по крайней мере, O(N*logN) времени.
Сортировка выбором
Сортировка выбором – это простой алгоритм O(N 2 ). Его задача – искать наименьший элемент, который затем меняется местами с элементом из начала списка. Затем находится из оставшихся элементов и меняется местами со вторым элементом. Процесс продолжается до тех пор, пока все элементы не займут свое конечное положение.
- Определяется наименьший элемент a7=1
- Меняется местами с первым 1 4 5 3 10 8 2
- В оставшемся снова ищется минимальный и меняется со вторым 1 2 5 3 10 8 4
- и т. д.
1 2 3 5 10 8 4
1 2 3 4 10 8 5
1 2 3 4 5 8 10
1 2 3 4 5 8 10
| For i = 1 To n — 1 Min = a(i) k_min = i For j = i + 1 To n If a(j) < Min Then Min = a(j) k_min = j End If Next a(k_min) = a(i) a(i) = Min Next | Для реализации этого алгоритма необходимы вложенные циклы For. Внешний цикл (по I) предназначен для последовательного фиксирования элементов массива, внутренний (по J) — осуществляет поиск минимума (максимума) и его позиции. После выхода из внутреннего цикла следует перестановка элементов. Последний элемент во внешнем цикле не рассматривается: он сам встанет на свое место. |
При поиске i-го наименьшего элемента алгоритм должен проверить каждый из N-I оставшихся. Время выполнения алгоритма равно N+(N-1)+(N-2)+…+1 или O(N 2 ).
Сортировка выбором работает достаточно хорошо со списками, где элементы расположены случайно или в прямом порядке, но для обратно сортированных списков производительность этого алгоритма немного хуже. Для поиска минимального элемента списка сортировка выбором выполняет следующую последовательность операторов:
Это не самый быстрый алгоритм, но он очень прост, а также быстро сортирует небольшие списки.
Сортировка вставкой
Сортировка вставкой – еще один алгоритм сложности O(N 2 ). Основан на внедрении в отсортированную часть массива элемента, следующего за этой частью, если он удовлетворяет условию сортировки. Алгоритм просматривает исходный список в порядке возрастания и ищет место, где необходимо вставить новый элемент. Затем он помещает новый элемент в найденную позицию.
На первом проходе второй элемент сравнивается с первым, на втором – третий элемент сравнивается с первым и вторым и т.д. Если проверяемый i+1-ый элемент удовлетворяет условию сортировки среди i элементов, то он вставляется на j-е место без нарушения порядка, т.е. элементы с индексами >=j и
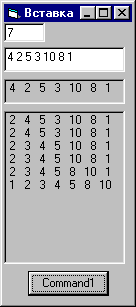 | For i = 2 To n ‘сравнение всегда начинается b = a(i): j = 1 ‘с первого Do While b > a(j) ‘определяется номер j = j + 1 ‘для вставки Loop For k = i To j + 1 Step –1 ‘освобождается a(k) = a(k — 1) ‘место для вставки Next k a(j) = b ‘осуществляется вставка For l = 1 To n Picture2.Print a(l); » «; Next Picture2.Print Next I End Sub Всего проходов n-1. |
Подобный алгоритм много времени тратит на поиск правильной позиции для нового элемента. Работает медленнее, чем сортировка выбором.
Пузырьковая сортировка
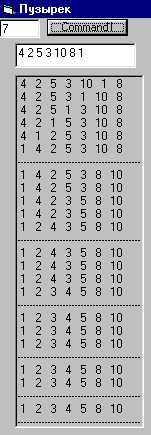
Пузырьковая сортировка – это алгоритм, предназначенный для сортировки списков, которые уже находятся в почти упорядоченном состоянии. Если это условие выполнено, то алгоритм выполняется очень быстро, за время порядка O(N). Если элементы изначально расположены в произвольном порядке, алгоритм выполняется за O(N 2 ) шагов.
При пузырьковой сортировке список просматривается до тех пор, пока не найдутся два смежных элемента, которые следуют не по порядку. Они меняются местами, и список продолжает исследоваться дальше. После первого прохода на первом месте (по возрастанию) окажется самый маленький элемент. Следующий проход будет осуществляться до этого элемента, т.е. сортируется оставшаяся часть массива. Алгоритм повторяет этот процесс, пока не упорядочит все элементы.
 |  |
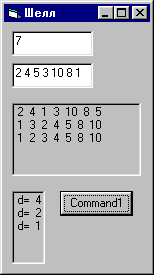
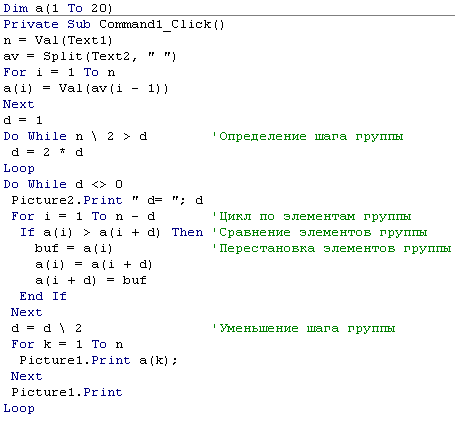
Сортировка методом Шелла
- N элементов массива разбивается на K групп, причем в группе не более 2 элементов, элементы располагаются на расстоянии D друг от друга. D – шаг группы.
- Производится сортировка в группах.
- Шаг группы D уменьшается вдвое.
- Повторяются пункты 2 – 3 до тех пор, пока шаг не станет меньше 1.
В разных вариантах метода Шелла может быть задана разная последовательность уменьшения шагов и способов определения начального значения D.Начальное значение шага D можно задать, как степень числа 2, таким образом, что D ≥ N/2. При больших значениях N время сортировки методом Шелла значительно меньше, чем в методе пузырька.
 |  |
Пирамидальная сортировка (бинарные деревья)
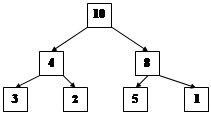
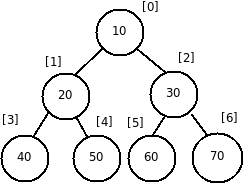
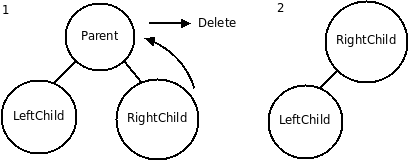
Пирамида – полное двоичное дерево, в котором каждый узел больше, чем его два дочерних. Оба дочерних узла, должны быть меньше, чем родительский, но любой из них может быть больше другого. Корневой узел всегда самый большой в пирамиде.
Любой массив можно представить в виде пирамиды, поместив первый элемент массива в корень пирамиды.
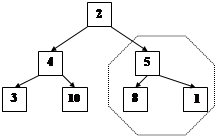 |
Поддерево, начинающееся в любом узле пирамиды, тоже является пирамидой.
Используя этот факт, можно построить пирамиду снизу вверх. Из каждого из поддеревьев с тремя узлами нужно сформировать пирамиду. Для этого нужно сравнить верхний узел с двумя его дочерними. Если любой из дочерних узлов больше, нужно поменять его с верхним узлом. Если оба дочерних узла больше, нужно поменять родительский с большим из дочерних. Этот шаг повторяется до тех пор, пока все поддеревья не станут пирамидами:
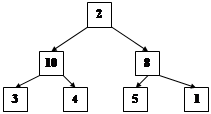 |
Затем, создаются более крупные пирамиды: маленькие пирамиды с вершинами 10 и 8 объединяются с элементом 2.
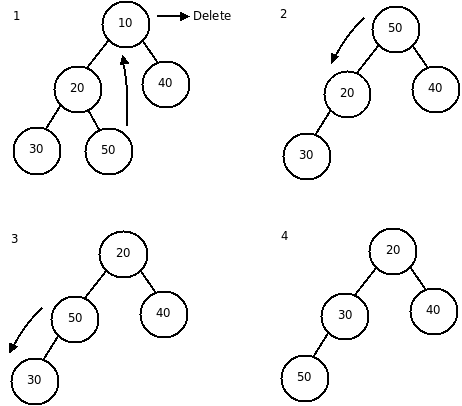
В итоге на самой вершине пирамиды оказывается максимальный элемент последовательности. Выкидываем его из пирамиды, а на его место ставим крайний справа элемент на нижнем уровне. Из оставшихся элементов снова строим пирамиду. На вершине получаем следующий наибольший элемент и т. д.
Дата добавления: 2021-01-21 ; просмотров: 192 ; Мы поможем в написании вашей работы!
© 2014-2023 — Студопедия.Нет — Информационный студенческий ресурс. Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав (0.03)
Источник
Теоретические сведения. Пирамида (Heap) – это структура данных, представленная в виде бинарного дерева, значения родительских узлов в котором меньше или равны
Пирамида (Heap) – это структура данных, представленная в виде бинарного дерева, значения родительских узлов в котором меньше или равны, значению любого из наследников.
В пирамидах существуют два вида упорядочения:
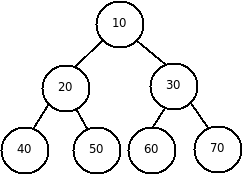
При упорядочении по возрастанию значение родительского узла меньше или равно любому из его наследников (рис. 1).
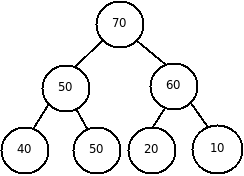
При упорядочении по убыванию значение родительского узла больше или равно любому из его наследников (рис. 2).
| Рис. 1. Пирамида, упорядоченная по возрастанию | Рис. 2. Пирамида, упорядоченная по убыванию |
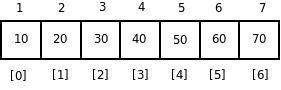
Пирамиду эффективней всего представить в виде одномерного массива, узлы которого имеют последовательную индексацию.
Для представления пирамиды в виде дерева, необходимо знать, как родительский узел связан с наследниками и как наследники связаны с родительским узлом.
Пусть i – номер родительского узла, тогда левый сын будет иметь индекс в массиве 2 i +1, а правый – 2 i +2. Индекс левого сына будет всегда нечетным, а правого – четным.
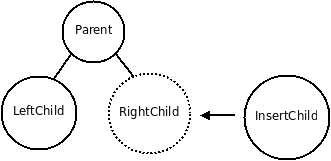
Пусть i – порядковый номер дочернего узла, тогда номер родительского узла можно найти по формуле: (.
Для левого сына всегда будет получаться целое число, а для правого сына значение необходимо округлить до наименьшего целого.
В языке C++ не нужно округлять до наименьшего целого. Это происходит автоматически при выполнении целочисленного деления.
В пирамиде используют две операции: вставка и удаление.
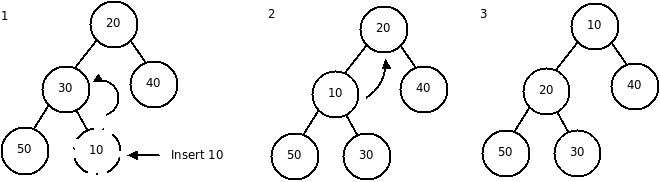
Вставка очередного узла всегда осуществляется в конец пирамиды.
После этого может произойти изменение структуры «пирамида», поэтому необходимо сравнить значение вставляемого узла с родительским узлом. Если значение данного узла меньше (больше) родительского, то вставляемый узел меняют с родительским узлом местами. И т.д. поднимаясь вверх по структуре «дерево».
Данная операция рассматривается отдельно, как перемещение узла вверх до тех пор, пока не будет достигнут корень дерева или не будет найдено правильное место узла в его структуре.
Операция удаления выполняется только для корня дерева, в котором будет всегда находиться минимальный (максимальный) элемент. После удаления корня, на его место помещают последний элемент в структуре «пирамида».
Однако при этом может нарушиться структура пирамиды. Поэтому вставленный узел сравнивается с его наследниками. Если он больше (меньше) любого из наследников, то он перемещается вместо наименьшего из них. Данная операция повторяется для всех остальных узлов и называется перемещением узла вниз. Она выполняется до тех пор, пока не будет достигнут конец дерева или пока не будет найдено место для вставки.
Пирамида является одним из самых эффективных и устойчивым методом сортировки элементов. Она является основой очередей приоритетов и используется в БД в качестве индексов.
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
Источник