- Лабораторная работа №3 (бинарные деревья)
- Комментарий от разработчиков программы
- Стоимость доработки программы
- Структура проекта
- Реализация задачи на языке С++
- Результаты работы программы
- Варианты индивидуальных заданий их стоимость реализации
- Образец выполнения (вариант №5)
- Условие задания
- Алгоритм решения задачи
- Подсчитать количество узлов на заданном уровне бинарного дерева
- 1 ответ 1
- Как найти количество вершин на заданном уровне бинарного дерева ( поиска )
- Как найти количество узлов бинарного дерева ( поиска )
Лабораторная работа №3 (бинарные деревья)
Необходимо написать модуль, содержащий решения $16$ задач для работы с бинарными деревьями, и программу, демонстрирующую работу этого модуля. Программа должна быть выполнена либо в качестве консольного приложения (тогда обязателен командно-текстовый интерфейс), либо иметь графический интерфейс пользователя.
При необходимости можно использовать вспомогательные функции. В разработанном модуле не должны применяться интерфейсные функции (исключение возможно только для функций вывода дерева).
Комментарий от разработчиков программы
Мы частично разработали решение данной задачи для всех студентов, изучающих данную тему. Программа реализована в среде MS Visual Studio на языке программирования C++ (консольный проект).
В коде учтены все пожелания и требования к данной задаче, выдвигаемые составителями. Соблюдены названия переменных, порядок выполнения операторов и пр.нюансы.
Закодированы следующие операции над бинарным деревом поиска:
void MakeBinaryTree(bintree** proot, const int pn)
Операции, имеющие желтоватый фон, — вспомогательные операции, которые так или иначе были использованы при кодировании основных операций обработки бинарного дерева поиска.
Стоимость доработки программы
$200$ рублей, если стек уже закодирован.
$700$ рублей, если стек не закодирован и его нужно кодировать.
$500$ рублей, если стек уже закодирован.
$1\ 200$ рублей, если стек не закодирован и его нужно кодировать.
$200$ рублей, если очередь уже закодирована.
$700$ рублей, если очередь не закодирована и ее нужно кодировать.
$500$ рублей, если очередь уже закодирована.
$1\ 200$ рублей, если очередь не закодирована и ее нужно кодировать.
Данная работа предполагает написание программы на языке C++. При заказе нужных вам операций над бинарным деревом поиска вы получите качественно написанную и хорошо прокомментированную программу.
➡ Дополнительно заказав алгоритм решения задачи (мы крайне рекомендуем это сделать), получите аккуратно оформленный отчет-алгоритм, поясняющий все тонкости решения поставленной задачи.
Структура проекта
В результате частичного кодирования данной задачи получился проект, состоящий из $3$ файлов:
- tree.h — пользовательские описания (типы данных и прототипы функций).
- tree.cpp — модуль для работы с бинарным деревом поиска.
- source.cpp — программа, демонстрирующая работу модуля tree.cpp.
Реализация задачи на языке С++
static const TCHAR * title = TEXT ( «Практикум на ЭВМ. Структуры данных и алгоритмы. С++. Лабораторная работа №3 (бинарное дерево поиска)» ) ;
cout
cout
cout
Результаты работы программы
| № | Смысл операции и результат |
| 1 | 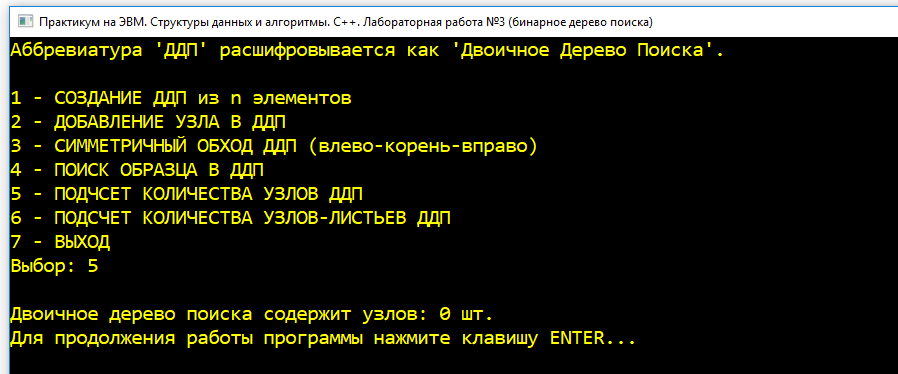 Попытка получить общее количество узлов в дереве (изначально дерево пустое). Попытка получить общее количество узлов в дереве (изначально дерево пустое). |
| 2 | 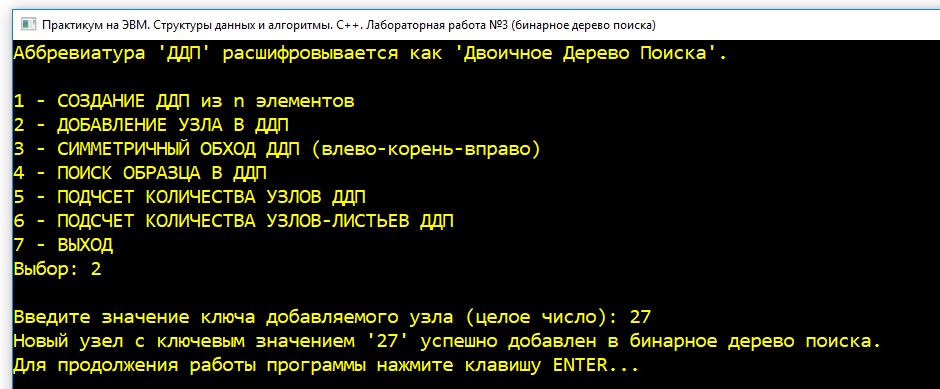 Добавление узла в дерево с ключом, равным $27$. Добавление узла в дерево с ключом, равным $27$. |
| 3 | 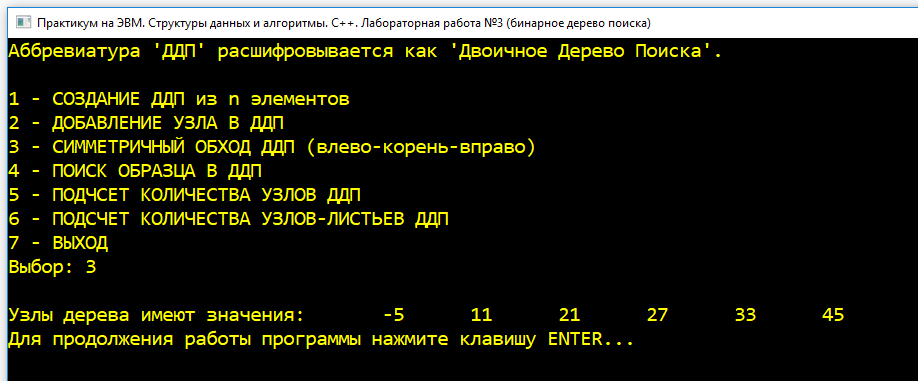 Добавляем последовательно узлы со значениями: $11$, $45$, $33$, $-5$, $21$. После этого печатаем узлы дерева на экран. Добавляем последовательно узлы со значениями: $11$, $45$, $33$, $-5$, $21$. После этого печатаем узлы дерева на экран. |
| 4 | 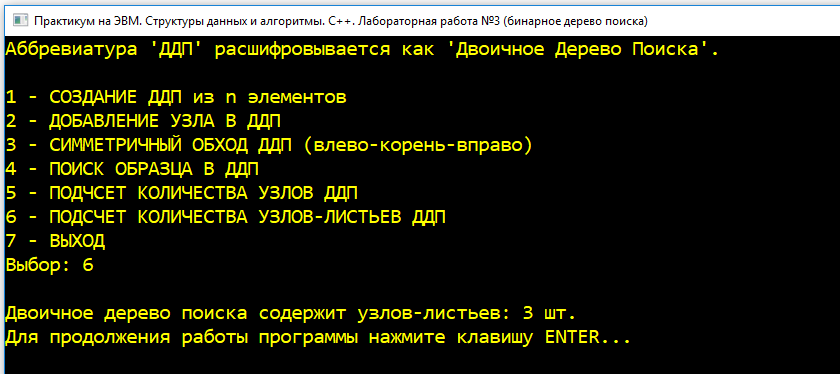 Попытка получить общее количество листьев в дереве. Попытка получить общее количество листьев в дереве. |
| 5 |  Создаем дерево, состоящее из $8$ узлов. Создаем дерево, состоящее из $8$ узлов. |
| 6 | 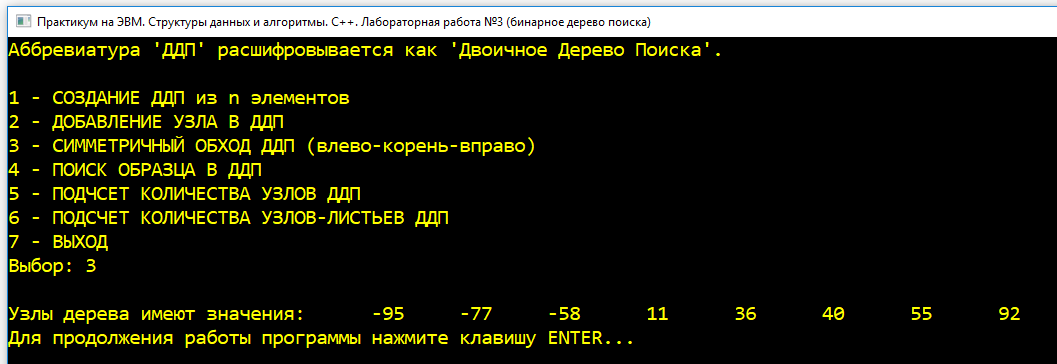 Печатаем узлы дерева на экран. Печатаем узлы дерева на экран. |
| 7 |  Завершаем работу с программой. Завершаем работу с программой. |
Варианты индивидуальных заданий их стоимость реализации
Задание для всех вариантов звучит так (или, возможно, немного изменено, так как могут быть разные издания учебного пособия):
За индивидуальную задачу при работе по БРС можно получить до 5 баллов. Для ее решения рекомендуется использовать подготовленный ранее программный модуль.
Бесплатно
(см. пример ниже)
Лабораторная работа $№3$ предполагает написание программы на языке C++. При заказе работы своего варианта вы получите качественно написанную и хорошо прокомментированную программу.
➡ Дополнительно заказав алгоритм решения вашей задачи (мы крайне рекомендуем это сделать), получите аккуратно оформленный отчет-алгоритм, поясняющий все тонкости решения поставленной задачи.
Образец выполнения (вариант №5)
Условие задания
Выведите номера вершин, у которых количество потомков в левом поддереве отличается от количества потомков в правом поддереве на $1$.
Алгоритм решения задачи
Прежде чем переходить непосредственно к кодированию данного задания, нужно провести его алгоритмизацию. Данный этап является обязательным и ни один профессиональный программист не опускает его в своей работе.
Предположим, что мы получили бинарное дерево поиска следующей конфигурации:
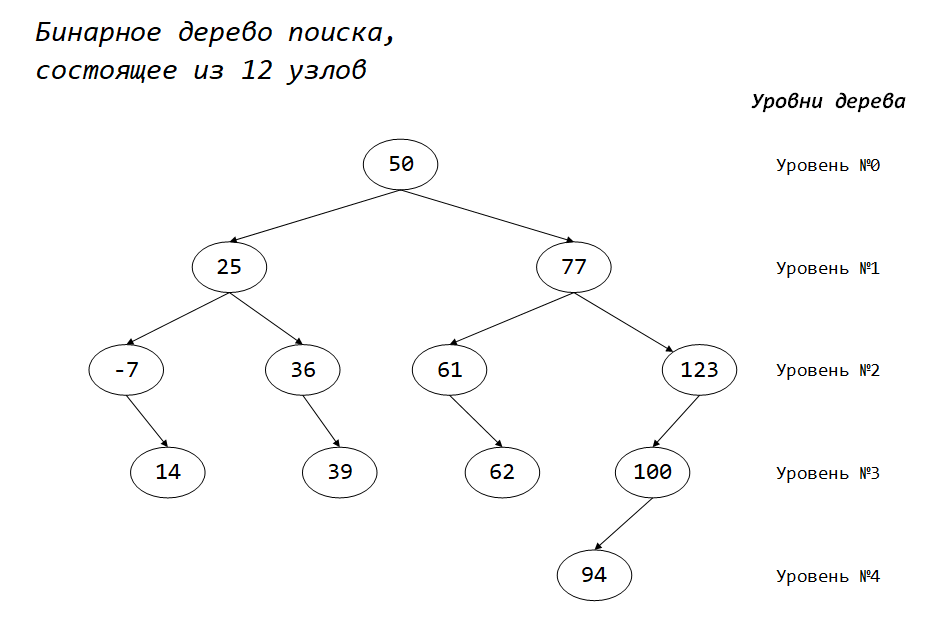 |
Данное дерево состоит из $12$ узлов, образующих $4$ уровня, кстати, является почти сбалансированным (для решения данной задачи это не важно).
Очевидно, что придется просмотреть все узлы данного дерева. Для этого можно воспользоваться любым из вариантов обхода дерева (прямой, обратный, симметричный). Выбираем симметричный порядок обхода, чтобы при печати номеров вершин они шли по возрастанию.
Далее нужно вспомнить, что в нашем распоряжении (в разработанном ранее модуле для работы с двоичным деревом поиска) есть замечательная функция, подсчитывающая количество узлов в заданном дереве/поддереве:
➡ Благодаря данной функции мы достаточно просто решим поставленную задачу! Начинаем последовательно сканировать в симметричном порядке все вершины дерева и для каждого узла подсчитывать количество потомков из левого и правого поддерева. Затем сравниваем модуль разности этих количеств на $1$, т к нам не важно, в каком из поддеревьев будет больше потомков на одного, главное, чтобы отличие было строго на один потомок.
Для приведенного дерева оранжевые узлы удовлетворяют этому условию:
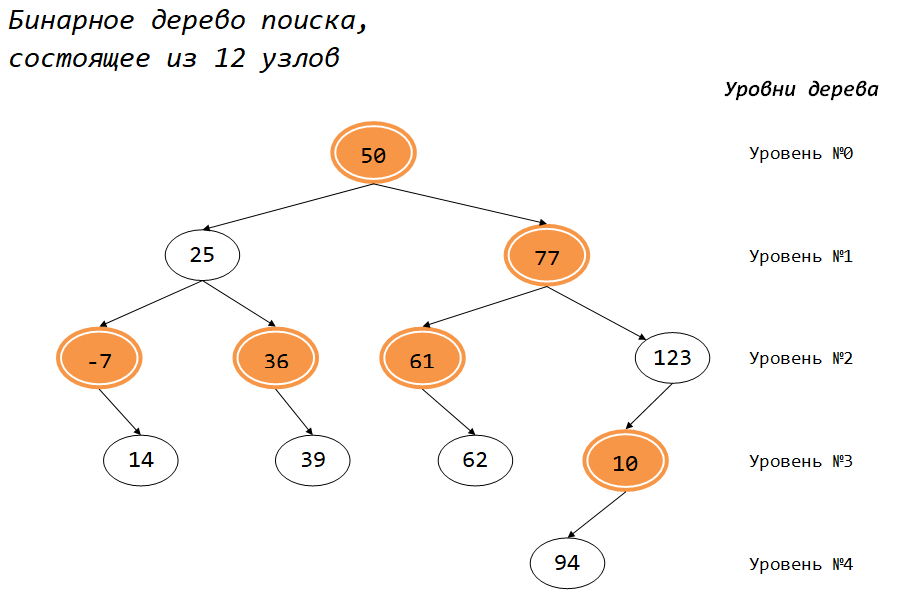 |
| Значение вершины | Количество потомков в левом поддереве | Количество потомков в правом поддереве | Разность | Условие |
| -7 | 0 | 1 | 1 | |
| 14 | 0 | 0 | 0 | |
| 25 | 2 | 2 | 0 | |
| 36 | 0 | 1 | 1 | |
| 39 | 0 | 0 | 0 | |
| 50 | 5 | 6 | 1 | |
| 61 | 0 | 1 | 1 | |
| 62 | 0 | 0 | 0 | |
| 77 | 2 | 3 | 1 | |
| 94 | 0 | 0 | 0 | |
| 100 | 1 | 0 | 1 | |
| 123 | 2 | 0 | 2 |
Источник
Подсчитать количество узлов на заданном уровне бинарного дерева
необходимо посчитать кол-во узлов на заданном уровне бинарного дерева, пыталась набросать функцию со счетчиками при рекурсивном обходе дерева, но понимаю, что счетчики таким образом работают неправильно. не могу никак придумать, как правильно это решить. Есть код самого класса и идеи для реализации метода на C#:
class BinaryTree //класс для хранения информации узла < public long? value < get; private set; >public BinaryTree left < get; set; >public BinaryTree right < get; set; >public void CountLevel (int level) < _CountLevel(this, level, 0, 0); >public void _CountLevel (BinaryTree currentNode, int level, int currentLevel, int n) //метод подсчета, level - заданный уровень дерева; currentLevel - номер текущего уровня; n - счетчик числа узлов < if (currentNode == null) < return; >if (currentLevel == level) n++; _CountLevel(currentNode.left, level, currentLevel + 1, n); _CountLevel(currentNode.right, level, currentLevel + 1, n); > > 1 ответ 1
Допустим, у нас есть класс узла дерева
public class TreeNode < public int Valpublic TreeNode Left public TreeNode Right > Метод, что считает кол-во узлов на уровне можно выразить так
public int CountNodesOnLevel(TreeNode root, int level)
var root = new TreeNode() < Left = new TreeNode() < Left = new TreeNode(), Right = new TreeNode() >, Right = new TreeNode() < Right = new TreeNode() >>; Console.WriteLine(CountNodesOnLevel(root, 2)); Источник
Как найти количество вершин на заданном уровне бинарного дерева ( поиска )
Хочу рассмотреть следующее двоичное дерево ( в данном случае — поисковое ):
Рисунок — обыкновенное двоичное поисковое дерево
➡ Для начала надо понять, как нумеруются уровни дерева, на каком уровне лежит корневая вершина и т.п.
Следующая картинка дает ответы на подобные вопросы:
Рисунок — уровни двоичного дерева
Из рисунка видно, что корневая вершина лежит на первом уровне. Иногда в теории алгоритмов нумерацию уровней бинарного дерева начинают с $0$. По-большему счету это непринципиально и мало влияет на логику алгоритма определения количества узлов на заданном уровне.
Визуально посчитаем количество вершин, а также их ключевые значения на каждом уровне рассматриваемого бинарного дерева и сведем информацию в сводную таблицу:
| # уровня | Количество вершин | Значения вершин |
| $1$ | $1$ | $52$ |
| $2$ | $2$ | $45,\ 125$ |
| $3$ | $3$ | $24,\ 88,\ 154$ |
| $4$ | $4$ | $61,\ 100,\ 132,\ 167$ |
| $5$ | $3$ | $82,\ 102,\ 155$ |
| $6$ | $2$ | $74,\ 118$ |
| $7$ | $0$ | $—$ |
💡 Но хочу напомнить, что моя задача — написать программную функцию, которая вычисляет количество вершин на заданном ( $N$-ом ) уровне двоичного дерева.
То есть меня мало интересуют значения вершин ( ключевые данные ), а лишь их количество. Из этого следует, что мне не важно, является бинарное дерево поисковым или нет. Поэтому сейчас покажу анонимное двоичное дерево аналогичной топологии:
Рисунок — уровни анонимного двоичного дерева ( поиска )
Например, пользователь «говорит», что хочет узнать количество вершин на $5$-ом уровне. Моя программная функция должна в качестве результата выдать ответ $3$, так как на уровне #$5$ находится три вершины:
Рисунок — на уровне #$5$ находится $3$ вершины
➡ Если пользователь сделает запрос по номеру уровня, которого не существует в двоичном дереве, то программа должна выдать ответ $0$. Например, уровня #17 в анализируемом анонимном двоичном дереве нет физически, поэтому и узлов на этом уровне также нет физически.
Кстати, в одной из своих статей-шпаргалок я показывал, как реализовать поуровневый вывод вершин бинарного дерева ( поиска ). Мне пришлось задействовать классическую структуру данных «Очередь» ( Queue, FIFO — First-In, First-Out ). Весь процесс был построен итеративно, то есть без рекурсии. В текущем алгоритме ( нахождения количества узлов на заданном уровне ) мне не придется прибегать к вспомогательным структурам данных и, думаю, все реализую рекурсивно в одной компактной функции.
💡 Основная идея алгоритма определения количества узлов двоичного дерева ( поиска ) на заданном ( $N$-ом ) уровне: так как до каждой вершины дерева существует строго один путь от корневой вершины ( корень лежит на уровне #$1$ ), то я буду рекурсивно перебирать все пути до тех пор, пока не будет достигнут заданный уровень или NULL.
Под перебором я понимаю стандартный обход двоичного дерева. Всего их существует $6$ штук. Я выберу LKP-обход ( симметричный левый, левый-корень-правый ).
Если в процессе обхода дерева я вышел на заданный уровень, то дальше спускаться по дереву смысла нет, поэтому это будет окончанием рекурсивного спуска для текущего пути и в качестве ответа верну из функции $1$.
В результате закодировал на языке «чистый» Си следующую функцию, а также поставил детальные комментарии к каждой строке кода:
Источник
Как найти количество узлов бинарного дерева ( поиска )
В этой статье-шпаргалке я хочу показать, как найти количество вершин в заданном двоичном дереве.
➡ Абсолютно не важно — является дерево поисковым или нет, главное требование к нему, чтобы оно было бинарным.
Хочу рассмотреть следующее анонимное двоичное дерево. Почему анонимное? Потому что все узлы этого дерева не имеют ни ключей, ни каких-либо данных. Для исследования алгоритма мне это не важно!
Рисунок — стандартное анонимное бинарное дерево ( поиска )
Посчитать «глазами» количество узлов в этом дереве, используя представленную картинку, не составляет труда. Очевидно, что данное двоичное дерево содержит $11$ узлов. Но мне нужна программная функция, которая выполняет всю эту работу за меня. Выполняет быстро, правильно и надежно.
Я люблю исследовать двоичные деревья ( в том числе и поиска ), когда отображены все связи ( ветви ) между узлами, а также показан указатель на корень дерева. Поэтому рассмотрю следующее изображение:
Рисунок — анонимное бинарное дерево с указанием всех ветвей
💡 А сейчас покажу основную идею алгоритма. Для этого я пронумерую все вершины ( в хаотичном порядке ) натуральными числами от $1$ до $n$, где $n$ — общее количество узлов двоичного дерева, а также выделю оранжевым цветом некоторые ветви. В итоге у меня получилась такая картина:
Рисунок — взаимосвязь количества ветвей и количества вершин двоичного дерева
➡ И теперь я хочу посчитать количество оранжевых ветвей и количество вершин в этом дереве. Оказывается эти количества равны друг другу и составляют число $11$.
Поэтому моя задача сводится к тому, чтобы посчитать количество оранжевых ребер. Это количество и будет ответом, так как оно будет равно количеству узлов бинарного дерева.
Другой важный момент заключается в том, что NULL-ветви при обходе дерева учитывать не нужно. То есть, если исследуется NULL-ребро необходимо искомое количество увеличивать на величину $0$.
И последний штрих: необходимо уловить связь между оранжевыми ребрами и числом рекурсивных вызовов функции, которая считает искомое количество. Общее количество рекурсивных вызовов будет равно общему числу всех связей, но, как мы раньше договорились, NULL-ветви учитываться не будут ( будет возвращаться для них число $0$ ).
В результате я закодировал на языке «чистый» Си следующую компактную рекурсивную функцию ( используется каскадная рекурсия ):
Источник






