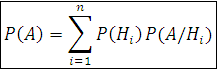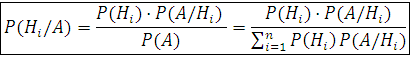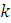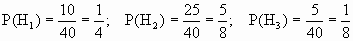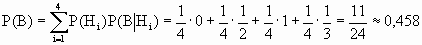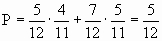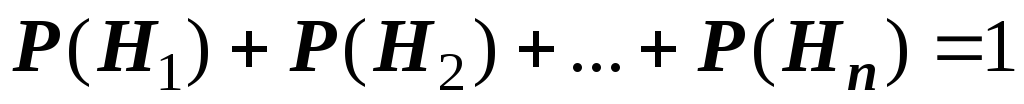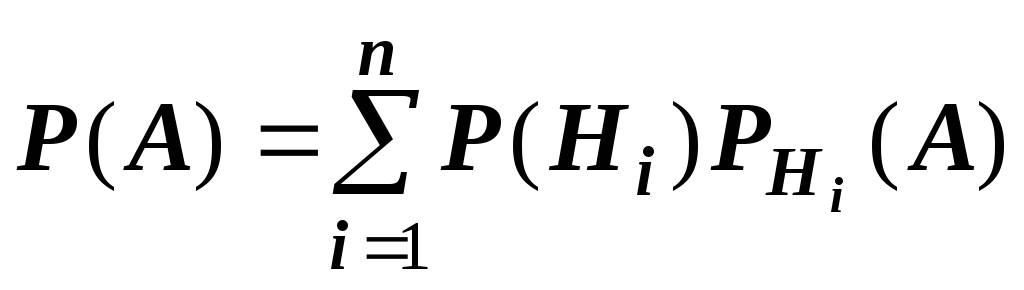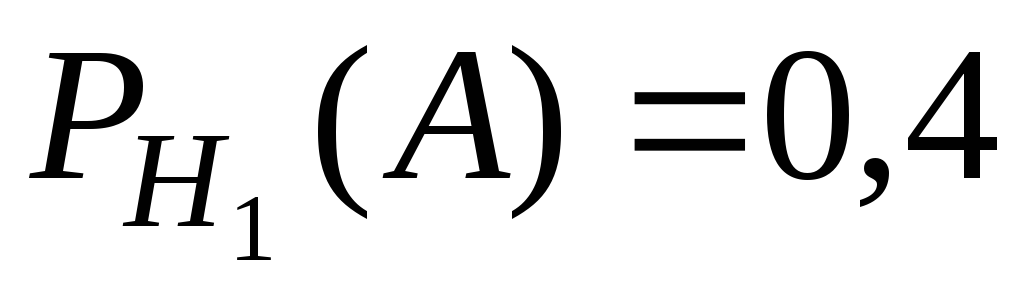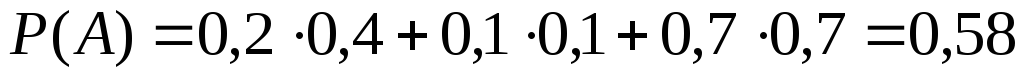Полная вероятность дерево вероятностей

5.5. Формула полной вероятности и формула Байеса

Рассмотрим п попарно несовместных событий H₁, H₂, . . . , H_n. Они образуют полную группу событий, если они попарно несовместны, а их сумма является достовер­ным событием, т.е.

H_i . Нj = Ø при i ≠ j и H₁ +H₂ + . . . + Н_n = Ω.

Такие события называются гипотезами.

Простейшим примером полной группы событий является произвольное событие А и его дополнение Ā. По теореме сложе­ния вероятностей, для полной группы событий справедливо ра­венство

Р(Н₁) + Р(Н₂) + . . .+ Р(Н_п) =1.

Примеры:

1. Пусть Ω = . Рассмотрим события H₁ = , H₂ = , H₃ = . Они попарно несовместны, а их сумма является дос­товерным событием Ω. Значит, Н₁, H₂, H₃ составляют полную группу событий. Для них Р(Н₁) = 5/10, Р(H₂) = 2/10, Р(Н₃) = 3/10, т.е. сумма их вероятностей равна 1.

2. В лесу растут деревья, среди которых 60 % берез, 10 % елей, и 30 % сосен. [3, c. 16]. Случайным образом выбира­ется для замера одно из деревьев. Обозначим гипотезы: Н₁ – «выбранное дерево – береза», H₂ – «выбранное дерево – ель», H₃ – «выбранное дере­во – сосна». Тогда события H₁, H₂, H₃ – попарно несовместны, Р(Н₁) = 0,6, Р(Н₂) = 0,1, Р(Н₃) = 0,3. Значит, гипотезы H₁, H₂, H₃ составляют полную группу событий. Сумма их вероятностей равна 1.

_______________________________________________________________________________

Пусть события H₁, H₂, . . ., Н_п образуют полную группу собы­тий. Тогда для любого события А имеет место формула полной вероятности:

Пример:

Рассмотрим предыдущий пример 2. Пусть при замере диаметра деревьев он оказался больше 15 см для 30 % берез, 40 % елей и 70 % сосен. Введем событие А – «диаметр случайно вы­бранного дерева больше 15 см». Найдем вероятность этого собы­тия. По условию примера, условные вероятности события А рав­ны: Р(А/H₁) = 0,3, P(А/H₂) = 0,4, Р (А/H₃) = 0,7. Тогда по формуле полной вероятности имеем:

Р(А) = P(H₁)P (А/H₁) + Р(Н₂)Р(А/H₂) + Р(Н₃)Р(А/H₃) = 0,6 . 0,3 + 0,1 . 0,4 + 0,3 . 0,7 = 0,43.

__________________________________________________________________

В формулу полной вероятности входят вероятности Р(Н₁), Р(Н₂), . . ., Р(Н_n), которые называются априорными. Это вероятности гипотез Н_i , вычисленные до опыта (a priori). Если событие А наступило, то эти вероятности изменяются. Это будут апостериорные условные вероятности, вычисленные после опыта (a posteriori) P(H₁/A), P_A(H₂/A), . . . , P_A(H_n/A). Они могут быть найдены по формуле Байеса:

Пример:_______________________________________________________________________

Пусть в условиях предыдущего примера диаметр случайно выбранного дерева оказался больше на 15 см, т.е. событие А наступило. Найти вероятность того, что измеренное дерево – береза. По формуле Байеса:

= = 0,42.

_____________________________________________________________

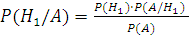
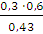
5.6. Формула Бернулли

Опыты называются независимыми, если вероятность исхода каждого опыта не зависит от того, какие исходы имели другие опыты. Пусть проводятся n независимых опытов, в результате которых может появиться событие A с вероятностью p и не появиться с вероятностью q, причем p+q = 1. Такая схема называется схемой Бернулли.

Пусть X – число появлений события А в n испытаниях Бернулли. Тогда вероятность того, что в серии из п независимых испытаний событие А появится ровно раз (Х=k) вычисляется по формуле Бернулли:

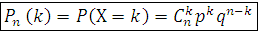
Пример:

Вероятность попадания в мишень для конкретного стрелка равна 0,7. Какова вероятность того, что из 10 выстрелов будет 4 попадания в мишень?

Воспользуемся формулой Бернулли приk = 4, n = 10, p = 0,7. Искомая вероятность равна = 0,0367.

________________________________________________________________

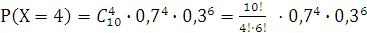
n испытаниях Бернулли наивероятнейшее число k₀ появления события А определяется неравенством

Пример:

Всхожесть семян некоторого растения имеет вероятность 0,8. Найти наиболее вероятное число проросших семян из 7 посеянных.

По формуле 8 ∙ 0,8—1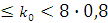, поэтому = 6.

Источник

9.4. Формула полной вероятности

В данном разделе мы рассмотрим более сложные задачи, имеющие большое практическое значение. Эти задачи встречается на практике в случае, если имеются несколько возможных сценариев развития событий (несколько вероятных гипотез). Известны как величины вероятности реализации каждого из сценариев, так и вероятность наступления интересующего нас события для любого из этих сценариев, а нас интересует, какова полная (совокупная) вероятность наступления интересующего нас события.

Предположим, что в результате опыта может произойти одно из n несовместных событий (гипотез) Н₁, H₂, . H_n. Пусть также имеется некоторое событие А и известны Р(Н_i) — вероятность гипотезы, P(A!H_i) — условная вероятность события А при этой гипотезе). Тогда вероятность события А вычисляется поформуле полной вероятности:

Пример.Из 40 деталей 10 изготовлены в первом цехе, 25 — во втором, а остальные — в третьем. Первый и третий цехи дают продукцию отличного качества с вероятностью 0,9, второй цех — с вероятностью 0,7. Какова вероятность того, что взятая наудачу деталь будет отличного качества?

По условию задачи P(A|H₁) = P(A|H₃) = 0,9, P(A|H₂)=0,7 По формуле полной вероятности находим искомую вероятность:

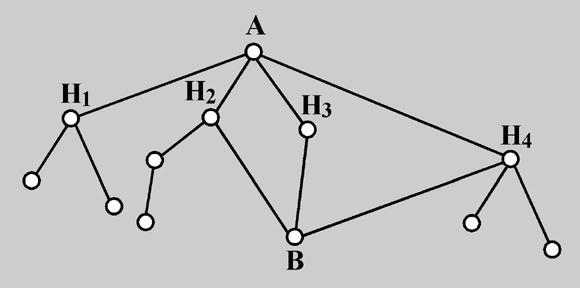
Пример.На рисунке изображена схема дорог. Найти вероятность того, что турист, вышедший из пункта А, попадет в пункт В, если на развилке он наугад выбирает любую дорогу (кроме обратной).

Решение: Обозначим H_i=i>, i=1, 2, 3, 4. Поскольку, выйдя из пункта А, он выбирает любую дорогу наугад, то P(H_i)=1/4, i=1, 2, 3, 4.

Исходя из схемы дорог, определяем, что P(B!H₁) = 0; P(B!H₂) =1/2; P(B!H₃) = 1; P(B!H₄) =1/3. Таким образом, по формуле полной вероятности

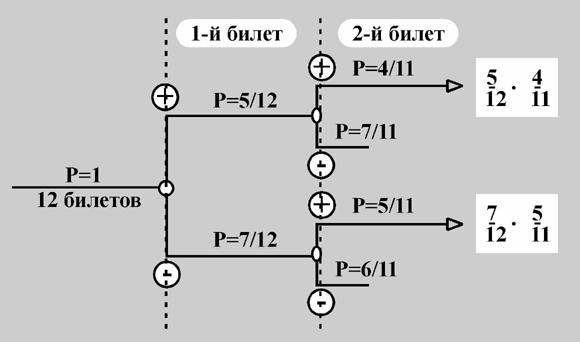
Пример. Из двенадцати лотерейных билетов пять выигрышных. Билеты вытягиваются по одному без возвращения. Какова вероятность того, что во второй раз вытянут выигрышный билет

Решение: Как обычно, вдоль каждой ветви «дерева вероятностей» значения вероятностей перемножаются, а затем значения на концах нужных веток между собой складываются. В результате получаем ответ:

После этого раздела Вам нужно выполнить первое письменное задание. Пожалуйста, пишите решение подробно, поясняйте все сделанные Вами предположения. ЗАДАНИЕ

1. В отделе найма персонала проводится тестирование на вакантную руководящую должность. Тест составлен из двух производственных ситуаций, не связанных между собой логически. По каждой ситуации предлагается три примера дальнейших действий, из которых надо выбрать один наилучший.

Вероятность того, что претендент знает ответ на первую часть теста равна Р1, вероятность того, что он знает ответ на вторую часть равна Р2. Допустим, что в случае, когда претендент не знает ответа, он принимает решение произвольно выбирать из трех предлагаемых вариантов наугад. Нарисуйте дерево вероятностей и посчитаете вероятности для разных сценариев развития событий. Прокомментируйте свои оценки. Какова вероятность того, что испытуемый знает ответы на обе части теста? Какова полная вероятность, что испытуемый ответит правильно на обе части теста? Можете ли Вы предложить свои способы повышения достоверности результатов такого тестирования?

Источник

4. Формула полной вероятности.

Определение. Если событие может происходить только с одним из событий

, которые образуют полную группу событий, то события называются гипотезами.

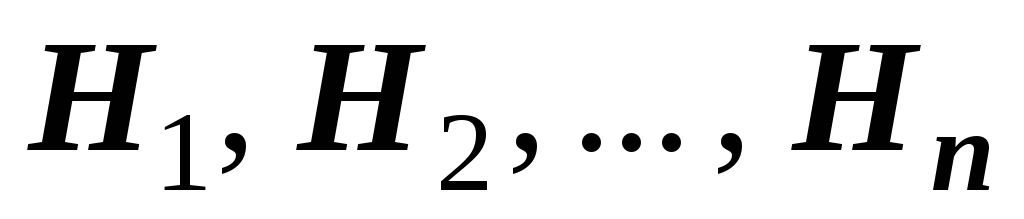
Поскольку события образуют полную группу событий, то сумма их вероятностей равна единице

,

Согласно следствию 3 из теоремы сложения. Это равенство следует применять при проверке правильности составления системы гипотез.

Теорема (формула полной вероятности). Если событие может произойти только с одной из гипотез , то вероятность события равна сумме произведений вероятностей гипотез на условные вероятности события, вычисленные при условии, что соответствующая гипотеза имела место

.

Доказательство.

Пример. В трех одинаковых урнах находятся шары. В первой урне находятся только белые шары, во второй только черные, а в третьей урне два черных и три белых шара.

Найти вероятность того, что наудачу выбранный шар из случайно выбранной урны является белым.

Запишем, прежде всего, условие задачи, вводя соответствующие обозначения.

Дано: событие состоит в том, что будет выбран белый шар.

Гипотеза состоит в том, что выбрана первая урна (состав урны: все белые шары).

Гипотеза состоит в том, что выбрана вторая урна (состав урны: все черные шары).

Гипотеза состоит в том, что выбрана третья урна (состав урны: 2 черных и 3 белых шара).

Найти:

Дерево вероятностей

Для решения задач, в которых решения принимаются в условиях стохастической неопределенности, удобно использовать так называемое «дерево вероятностей».

Определение. Деревом вероятностей называется графический метод, который показывает последовательность стратегических решений и предполагаемые последовательности действий при каждом возмож­ном блоке случайных обстоятельств.

Построение дерева решения начинается с первого решения и продвигается вперед через ряд последовательных событий и решений, при этом вероятностные события обозначаются кружками, а принимаемые решения квадратиками. Ответвления из квадратиков представляют стратегии, а ответвления из кружков — внешние условия. При каждом решении или событии у дерева вероятностей появляются ответвления, которые пока­зывают соответственно возможное направление действий до тех пор, пока, наконец, все логиче­ские последовательности решений и вытекающие из них события не будут вычерчены. Отметим, что ответвления из кружков имеют вероятности, причем сумма вероятностей для всех ответвлений, вытека­ющих из любого кружка, должна равняться единице.

Из формулы полной вероят­ности следует, что для вычисления вероятности события необ­ходимо осуществить перебор всех путей, ведущих к результиру­ющему событию ; вычислить и расставить на соответствующих путях вероятности того, что движение будет происходить поданному пути, и вероятности того, что на данном пути бу­дет достигнуто конечное событие . Затем вероятности, стоящие на одном пути, перемножаются, а результаты, полученные для раз­личных путей, складываются.

Каждое из условий может, в свою очередь, делиться на несколько дополнительных условий или гипотез, т.е. на каждом этапе оно допускает неограниченное число ветвлений схемы, поэтому при решении задач более удобно пользоваться не самой формулой полной вероятности, а графической схемой полной вероятности или соответствующим деревом вероятностей.

Пример. Трое преподавателей принимают экзамен в группе из 30 человек, причем первый опрашивает 6 студентов, второй — 3, а третий — 21 студента (выбор студентов производится случай­ным образом из списка). Отношение трех экзаменаторов к слабо подготовившимся различное: шансы таких студентов сдать эк­замен у первого преподавателя равны 40 %, у второго — только 10 %, зато у третьего — 70 %. Найти вероятность того, что слабо подготовившийся студент сдаст экзамен. Решение. Обозначим через ,— гипотезы, состоящие в том, что слабо подготовившийся студент отвечал первому, второму и третьему экзаменатору соответственно. По условию задачи

Пусть событие состоит в том, что слабо подготовившийся студент сдал эк­замен. Тогда по условию задачи

.

По формуле полной вероятности получаем

.

Построим для рассматриваемой задачи дерево решений

Источник