структуры данных заочники 2013 / Литература / методичка структуры данных си
Для взвешенных графов недостаточно просто указать, есть ли связь между вершинами. Требуется еще хранить в памяти «вес» каждого ребра, например, стоимость проезда или длину пути. Для этого используется весовая матрица . Весовая матрица графа с N вершинами – это матрица размером N на N , где каждый элемент с индексами (i,j) равен “весу” ребра из вершины i в вершину j .
| б) | ||||||||||
| A | B | C | D | E | A | 5 | B | |||
| A | 0 | 5 | 10 | 12 | 0 | 10 | 12 | |||
| B | 5 | 0 | 0 | 7 | 9 | C | 9 | 7 | ||
| C | 10 | 0 | 0 | 8 | 0 | |||||
| D | 12 | 7 | 8 | 0 | 0 | 8 | ||||
| E | D | |||||||||
| E | 0 | 9 | 0 | 0 | 0 | |||||
Задача Прима-Краскала Формулировка задачи Задача. Дана плоская страна и в ней n городов с известными координатами. Нужно соединить все города телефонной сетью так, чтобы длина телефонных линий была минимальная. Город будем изображать узлом (точкой). Телефонные линии могут разветвляться только на телефонных станциях, а не в чистом поле. Поскольку требуется линия минимальной общей длины, в ней не будет циклов, потому что иначе можно было бы убрать одно звено цикла и станции по-прежнему были бы связаны. В терминах теории графов эта задача звучит так: Дан граф с n вершинами; длины ребер заданы матрицей
29
| Программирование на языке Си | К. Поляков, 1995-200 2 |
Подобным образом, если оптимальное решение строится по шагам, обычно нельзя выбирать на каждом этапе «самое вкусное» — за это придется расплачиваться на последних шагах. Такие алгоритмы называют жадными . Решение Удивительно, но для непростой задачи Прима-Краскала жадный алгоритм дает точное оптимальное решение. Алгоритм формулируется так: В цикле n-1 раз выбрать из оставшихся ребер самое короткое ребро, которое не образует цикла с уже выбранными. Как же проследить, чтобы не было циклов? Оказывается очень просто: в самом начале покрасим все вершины в разные цвета и затем, выбрав очередное ребро между вершинами i и j , где i и j имеют разные цвета, перекрасим вершину j и все соединенные с ней (то есть имеющие ее цвет) в цвет i . Таким образом, при выборе ребер, соединяющих вершины разного цвета, цикл не возникнет никогда, а после n-1 шагов все вершины будут иметь один цвет. Для записи информации о ребрах введем структуру struct rebro < int i, j; >; 
вершины, которые соединены причем будем считать, что в паре номер первой вершины i меньше, чем номер второй j . Приведенная ниже программа действует по следующему «жадному» алгоритму: 1. Покрасить все вершины в разные цвета. 2. Сделать n-1 раз в цикле выбрать ребро (i,j) минимальной длины, соединяющее вершины разного цвета; запомнить его в массиве ребер; перекрасить все вершины, имеющие цвет j , в цвет i. 3. Вывести результат.
| const | N = 5; | ||
| void main() | |||
| int | D[N][N], Col[N], i, j, | ||
| k, Dmin, jMin, iMin, col_j; | |||
| rebro Reb[N-1]; | |||
| . | // здесь надо ввести матрицу D | ||
| for ( i = 0; i < N; i ++ ) | покрасить все вершины | ||
| Col[i] = i; | в разные цвета | ||
| for ( k = 0; k < N-1; k ++ ) | |||
| Dmin = 30000; | |||
| for ( i = 0; i < N-1; i ++ ) | |||
| for ( j = i+1; j < N; j ++ ) | |||
| if ( Col[i] != Col[j] && D[i][j] < Dmin ) | |||
| Dmin = D[i][j]; | |||
| iMin = i; | найти самое короткое ребро, не | ||
| jMin = j; | образующее циклов | ||
| > | |||
| Reb[k].i = iMin; | запомнить найденное ребро | ||
| Reb[k].j = jMin; | |||
| 30 | |||||
| IV. Динамические структуры данных | К. Поляков, 1995-2002 | ||||
| col_j = Col[jMin]; | |||||
| перекрасить все вершины, | |||||
| for ( i = 0; i < N; i ++ ) | |||||
| цвет которых совпадает с | |||||
| if ( Col[i] == col_j ) | |||||
| цветом вершины jMin | |||||
| Col[i] = Col[iMin]; | |||||
| > | |||||
. // здесь надо вывести найденные ребра > Дополнительно можно рассчитывать общую длину выбранных ребер, но это не меняет принципиально алгоритм. Этот алгоритм требует памяти порядка n 2 (обозначается O(n 2 ) , то есть при увеличении n в 2 раза объем требуемой памяти увеличивается в 4 раза). Его временная сложность – O(n 3 ) , то есть при увеличении n в 2 раза время вычислений увеличивается в 8 раз (надо просмотреть O(n 3 ) чисел и сделать это n-1 раз). Кратчайший путь Формулировка задачи Задача. Задана сеть дорог между населенными пунктами (часть из них могут иметь одностороннее движение). Требуется найти кратчайший путь между двумя заданными пунктами. Обычно задачу несколько расширяют и находят сразу кратчайшие пути от заданной вершины ко всем остальным. В терминах теории графов задача выглядит так: В сети, где часть дорог имеет одностороннее движение, найти кратчайшие пути от заданной вершины ко всем остальным. Алгоритм Дейкстры Ниже описывается алгоритм, предложенный Дейкстрой в 1959 г. Дана матрица длин дуг между вершинами, если дуги между вершинами i и j нет, то d ij = . Если сеть образуют n вершин, то для реализации алгоритма требуется три массива длиной n : 1. Массив , в котором a i =0 , если вершина i еще не рассмотрена, и a i =1 , если вершина i уже рассмотрена. 2. Массив , в котором b i — текущее кратчайшее расстояние от выбранной стартовой вершины x до вершины i . 3. Массив , в котором c i — номер предпоследней вершины в текущем кратчайшем пути из выбранной стартовой вершины x до вершины i . Сам алгоритм состоит из трех этапов: инициализации, основного цикла и вывода результата. Инициализация Пусть x — номер выбранной стартовой вершины. 1. Заполним весь массив a значением 0 (пока ни одна вершина не рассмотрена). 2. В i -ый элемент массива b запишем расстояние от вершины x до вершины i (если пути нет, то оно равно , в программе укажем очень большое число). 3. Заполним весь массив c значением x (пока рассматриваем только прямые пути от x к i ). 4. Рассмотрим стартовую вершину: присвоим a[x]=1 и c[x]=0 (начало всех путей).
Источник
4.4.4. Представление выражений с помощью деревьев
С помощью деревьев можно представлять произвольные арифметические выражения. Каждому листу в таком дереве соответствует операнд, а каждому родительскому узлу — операция. В общем случае дерево при этом может оказаться не бинарным.
Однако если число операндов любой операции будет меньше или равно двум, то дерево будет бинарным. Причем если все операции будут иметь два операнда, то дерево окажется строго бинарным.
Рис.4.16. Представление арифметического выражения произвольного вида в виде дерева.
Рис. 4.17. Представление арифметического выражения в виде бинарного дерева
Бинарные деревья могут быть использованы не только для представления выражений, но и для их вычисления. Для того чтобы выражение можно было вычислить, в листьях записываются значения операндов.
Затем от листьев к корню производится выполнение операций. В процессе выполнения в узел операции записывается результат ее выполнения. В конце вычислений в корень будет записано значение, которое и будет являться результатом вычисления выражения.
Помимо арифметических выражений с помощью деревьев можно представлять выражения других типов. Примером являются логические выражения. Поскольку функции алгебры логики определены над двумя или одним операндом, то дерево для представления логического выражения будет бинарным
Рис.4.18. Вычисление арифметического выражения с помощью бинарного дерева
Рис. 4.19. Представление логического выражения в виде бинарного дерева
4.5. Представление сильноветвящихся деревьев
До сих пор мы рассматривали только способы представления бинарных деревьев. В ряде задач используются сильноветвящиеся деревья. Каждый элемент для представления бинарного дерева должен содержать как минимум три поля — значение или имя узла, указатель левого поддерева, указатель правого поддерева. Произвольные деревья могут быть бинарными или сильноветвящимися. Причем число потомков различных узлов не ограничено и заранее не известно.
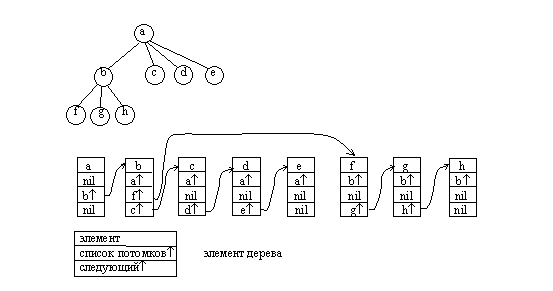
Тем не менее, для представления таких деревьев достаточно иметь элементы, аналогичные элементам списковой структуры бинарного дерева. Элемент такой структуры содержит минимум три поля: значение узла, указатель на начало списка потомков узла, указатель на следующий элемент в списке потомков текущего уровня. Также как и для бинарного дерева необходимо хранить указатель на корень дерева. При этом дерево представлено в виде структуры, связывающей списки потомков различных вершин. Такой способ представления вполне пригоден и для бинарных деревьев.
Представление деревьев с произвольной структурой в виде массивов может быть основано на матричных способах представления графов.
Рис.4.20. Представление сильноветвящихся деревьев в виде списков
4.6. Применение сильноветвящихся деревьев
Один из примеров применения сильноветвящихся деревьев был связан с представлением арифметических выражений произвольного вида. Рассмотрим использование таких деревьев для представления иерархической структуры каталогов файловой системы. Во многих файловых системах структура каталогов и файлов, как правило, представляет собой одно или несколько сильноветвящихся деревьев. В файловой системе MS Dos корень дерева соответствует логическому диску. Листья дерева соответствуют файлам и пустым каталогам, а узлы с ненулевой степенью — непустым каталогам.
Рис.4.21. Представление логической структуры каталогов и файлов в виде сильноветвящегося дерева.
Для представления такой структуры используем расширение спискового представления сильноветвящихся деревьев. Способы представления деревьев, рассмотренные ранее, являются предельно экономичными, но не очень удобными для перемещения по дереву в разных направлениях. Именно такая задача встает при просмотре структуры каталогов. Необходимо осуществлять «навигацию» — перемещаться из текущего каталога в каталог верхнего или нижнего уровня, или от файла к файлу в пределах одного каталога.
Для облегчения этой задачи сделаем списки потомков двунаправленными. Для этого достаточно ввести дополнительный указатель на предыдущий узел «last». С целью упрощения перемещения по дереву от листьев к корню введем дополнительный указатель на предок текущего узла «up». Общими с традиционными способами представления являются указатели на список потомков узла «down» и следующий узел «next».
Для представления оглавления диска служат поля имя и тип файла/каталога. Рассмотрим программу, которая осуществляет чтение структуры заданного каталога или диска, позволяет осуществлять навигацию и подсчет места занимаемого любым каталогом.
Источник