Построение кода прюфера по дереву

Алгоритм построения кода Прюфера по дереву

Вход: дерево с n вершинами.

Выход: код Прюфера длины n – 2.

Выбрать вершину v – лист дерева с наименьшим номером;

Добавить номер единственного соседа v в последовательность кода Прюфера;

Удалить вершину v из дерева;

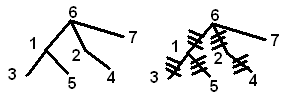
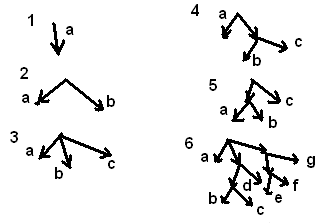
Пример 1. Построение всех кодов Прюфера длины 2. Для этого следует рассмотреть все возможные деревья из 4 вершин. Под каждым деревом приведен соответствующий код.

Алгоритм составления дерева по коду:

1.Выписываем висячие вершины, всего вершин на 2 больше чем значений в коде дерева.

2. находим наименьшее натуральное число, которое не встречается в последовательности.

3. это число – номер вершины, которую необходимо соединить с вершиной, которая встречается первой в коде.

4. находим следующее число.

Рассмотрим применение данного алгоритма на примере.

Пример 1. Постройте дерево, которому соответствует код

1. Выписываем висячие вершины. Всего вершин на 2 больше чем значений в коде дерева, в данном случае такими будут 3,4,5,6,7.

2. Вершину с минимальным номером (3) соединяем с первым значением кода (1).

3. Поскольку вершина (1) еще встречается в коде , то соединяем следующую висячую вершину (4) с вершиной из кода (2).

Дальше вершины (2) больше нет в коде, потому она становится висячей с наименьшим номером, потому следующим шагом я соединяю ее (2) со следующим значением кода (1).

Далее 6 – 7. Код закончился, осталась 6. Соединяем ее с 1.

Пример 2. Построить дерево по к . Смотреть решение »

Задана матрица инцидентности неориентированного графа G:

Источник

3.5. Код Прюфера.

Немецкий математик К.Прюфер изобрёл способ представления любых деревьев и ордеревьев. Изложим алгоритм построения кода Прюфера.

Пусть имеется дерево с n пронумерованными вершинами. В списке всех вершин слева направо ищем первую висячую вершину. Пусть это a_1. Ищем единственную вершину b₁ с которой смежна a₁. Величину b₁ заносим в новый список – будущий код Прюфера, а вершину a₁ вычеркиваем и из списка, и из дерева. Этот процесс повторяем n-2 раза. В результате получим новый список. 1, b₂,…, b_n-2> – это и есть код Прюфера. Заметим, что в процессе построения дерево все время уменьшается, и возникают новые висячие вершины

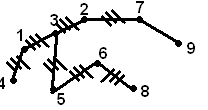
Построить код Прюфера для дерева.

В этом списке слева направо ищем первую висячую.

Доказано, что код Прюфера определяет дерево однозначно. Более того, любой список < b₁, b₂. b_n-2> чисел от 1 до n является кодом Прюфера некоторого дерева.

Восстановить дерево по коду Прюфера.

Введем понятие неприкосновенной вершины: если вершина встречается в коде Прюфера дальше, то она неприкосновенна

Д обавляем оставшиеся вершины.

Общее число деревьев с n пронумерованными вершинами равно n n -2 /

Таких деревьев ровно столько, сколько кодов Прюфера. b – число от 1 до n.

По правилу произведения n n-2

Например, для n=5, получим 5 5-2 =152 раз.

3.6. Обход деревьев.

Часто необходимо обойти все вершины дерева или ордерева не хаотично, а по определённому алгоритму.

Самые простые алгоритмы обхода для бинарного ордерева. Из 3 на выбор.

1)Прямой метод – обойти корень, затем левое поддерево, затем правое (КЛП)

Этот принцип соблюдается в любой момент времени.

2)Обратный метод: обойти левое поддерево, корень, правое поддерево (ЛКП)

3)Концевой метод: обойти левое поддерево, правое, корень (ЛПК)

Обойти 3 способам данное бинарное дерево (не менее 10 вершин)

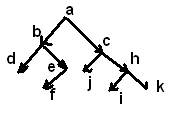
1 ) Прямой (КЛП) a b d e f c g h I k

2) Обратный (ЛКП) d b f e a g c I h k

3) Концевой (ЛПК) d f e b g I k h c a

Для не бинарных деревьев и ордеревьев алгоритм гораздо сложнее.

3.7. Деревья и списки.

Бытовое понятие списков всем известно, но в информатике имеется формальное понятие списка.

Опр. Назовем атомом любой неделимый объект (букву, цифру и т.д.). Списками называется последовательность атомов и списков, разделенных запятыми и заключенными в общие скобки.

Это так называемая рекурсивное определение (использующие само себя). В математике это запрещается, а информатике широко применяется.

Каждому списку можно сопоставить ордерево, действуя по правилу

Атомом или списком, заключенным в общие скобки, соответствует общая безымянная вершина, потомками которой они являются.

П ример.

Видим, что атомам соответствуют только висячие вершины дерева. Поэтому обратная связь такова: каждому дереву соответствует список его висячих вершин.

Вводится понятие глубины списка: наибольшее число вложенных друг в друга скобок.

При этом глубина списка совпадает с глубиной соответствующего дерева (число уровней).

Источник

Коды Прюфера

Кодирование Прюфера переводит помеченные деревья порядка [math]n[/math] в последовательность чисел от [math]1[/math] до [math]n[/math] по алгоритму:
Пока количество вершин больше двух:

1. Выбирается лист [math]v[/math] с минимальным номером.
2. В код Прюфера добавляется номер вершины, смежной с [math]v[/math] .
3. Вершина [math]v[/math] и инцидентное ей ребро удаляются из дерева.

Полученная последовательность называется кодом Прюфера (англ. Prüfer code) для заданного дерева.

Номер вершины [math]v[/math] встречается в коде Прюфера тогда и только тогда, когда [math]v[/math] не является листом, причём встречается этот номер к коде дерева в точности [math]\deg v — 1[/math] раз.

1. Вершина с номером [math]n[/math] не может быть удалена, следовательно на последнем шаге у неё была смежная вершина, и число [math]n[/math] встретилось в коде.
2. Если вершина не является листом, то у неё на некотором шаге была смежная вершина [math]-[/math] лист, следовательно номер этой вершины встречается в коде.
3. Если вершина является листом с номером меньше [math]n[/math] , то она была удалена до того, как был удален её сосед, следовательно её номер не встречается в коде.

По любой последовательности длины [math]n — 2[/math] из чисел от [math]1[/math] до [math]n[/math] можно построить помеченное дерево, для которого эта последовательность является кодом Прюфера.

Доказательство проведем по индукции по числу [math]n[/math]
База индукции:

[math]n = 1[/math] [math]-[/math] верно.

Пусть для числа [math]n[/math] верно, построим доказательство для [math]n+1[/math] :

Пусть у нас есть последовательность: [math]A = [a_1, a_2, . a_].[/math]

Кодирование Прюфера задаёт биекцию между множествами помеченных деревьев порядка [math]n[/math] и последовательностями длиной [math]n — 2[/math] из чисел от [math]1[/math] до [math]n[/math]

Следствием из этой теоремы является формула Кэли.

Пример построения кода Прюфера

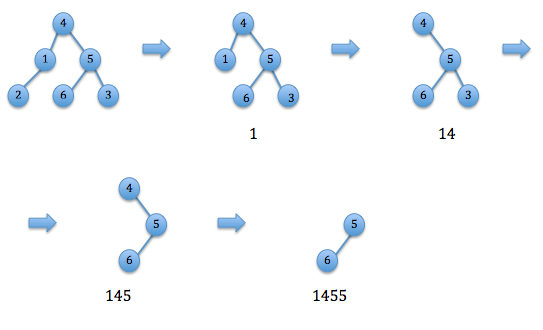
Алгоритм декодирования кодa Прюфера

В массиве вершин исходного дерева [math]V[/math] найдём вершину [math]v_[/math] с минимальным номером, не содержащуюся в массиве с кодом Прюфера [math]P[/math] , т.е. такую, что она является листом или концом уже добавленного в граф ребра, т.е. она стала листом в процессе построения кода Прюфера (по первому пункту построения). Вершина [math]p_1[/math] была добавлена в код Прюфера как инцидентная листу с минимальным номером (по второму пункту построения), поэтому в исходном дереве существует ребро < [math]p_1[/math] , [math]v_[/math] >, добавим его в список ребер. Удалим первый элемент из массива [math]Р[/math] , а вершину [math]v_[/math] — из массива [math]V[/math] т.к. она больше не может являться листом (по третьему пункту построения). Будем выполнять вышеуказанные действия, пока массив [math]P[/math] не станет пустым. В конце работы алгоритма в массиве [math]V[/math] останутся две вершины, составляющие последнее ребро дерева (это следует из построения).

Реализация

# P - код Прюфера # V - вершины function buildTree(P, V): while not P.empty(): u = P[0] v = min(x [math]\in[/math] V: P.count(x) == 0) G.push() P.erase(0) V.erase(indexOf(v)) G.push() return G

Пример декодирования кода Прюфера

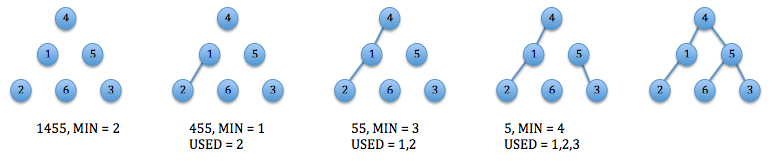
См. также

Источник

Код Прюфера

Дерево – частный случай графа. Деревья широко применяются в программировании. Дерево – это связный граф без циклов. Дерево называется помеченным, если каждой вершине соответствует уникальная метка. Обычно это число.

Определение. Построение кода Прюфера для заданного дерева

Код Прюфера – это способ взаимно однозначного кодирования помеченных деревьев с n вершинами с помощью последовательности n-2 целых чисел в отрезке [1,n]. То есть, можно сказать, что код Прюфера – это биекция между всеми остовными деревьями полного графа и числовыми последовательностями.

Данный способ кодирования деревьев был предложен немецким математиком Хайнцом Прюфером в 1918 году.

Рассмотрим алгоритм построения кода Прюфера для заданного дерева с n вершинами.

На вход подается список ребер. Выбирается лист дерева с наименьшим номером, затем он удаляется из дерева, и к коду Прюфера добавляется номер вершины, которая была связана с этим листом. Эта процедура повторяется n-2 раза. В конце концов, в дереве останется только 2 вершины, и алгоритм на этом завершается. Номера оставшихся двух вершин в код не записываются.

Таким образом, код Прюфера для заданного дерева – это последовательность из n-2 чисел, где каждое число – номер вершины, связанной с наименьшим на тот момент листом – то есть это число в отрезке [1,n].

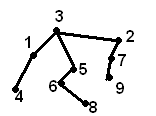
Пример

Исходное дерево

Код Прюфера: 1

Код Прюфера: 1 5

Код Прюфера: 1 5 2

Код Прюфера: 1 5 2 6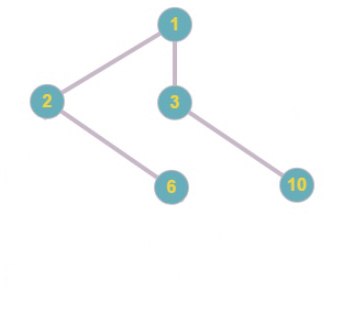

Код Прюфера: 1 5 2 6 6

Код Прюфера: 1 5 2 6 6 2

Код Прюфера: 1 5 2 6 6 2 1

Код Прюфера: 1 5 2 6 6 2 1 3

Восстановление дерева по его коду Прюфера

Рядом с задачей построения кода Прюфера стоит задача восстановления закодированного дерева. Будем рассматривать алгоритм восстановления дерева со следующими условиями: на вход подается последовательность цифр (вершин), которая представляет код Прюфера, результатом будет список ребер дерева. Таким образом, задача будет решена.

Рассмотрим алгоритм декодирования подробно. Помимо кода нам нужен список всех вершин графа. Мы знаем, что код Прюфера состоит из n-2 вершин, где n – это число вершин в графе. То есть, мы можем по размеру кода определить число вершин в закодированном дереве.

В результате, в начале работы алгоритма мы имеем массив из кода Прюфера размера n-2 и массив всех вершин графа: [1… n]. Далее n-2 раза повторяется такая процедура: берется первый элемент массива, содержащего код Прюфера, и в массиве с вершинами дерева производится поиск наименьшей вершины, не содержащейся в массиве с кодом. Найденная вершина и текущий элемент массива с кодом Прюфера составляют ребро дерева. Данные вершины удаляются из соответствующих массивов, и описанная выше процедура повторяется, пока в массиве с кодом не закончатся элементы. В конце работы алгоритма в массиве с вершинами графа останется две вершины, они составляют последнее ребро дерева. В результате получаем список всех ребер графа, который был закодирован.

Пример
Восстановим дерево по коду Прюфера, который был получен в примере кодирования.

Первый шаг
Код Прюфера: 1 5 2 6 6 2 1 3
Массив вершин дерева: 1 2 3 4 5 6 7 8 9 10
Минимальная вершина, не содержащаяся в коде Прюфера – это 4
Список ребер: 1 4

Второй шаг
Код Прюфера: 1 5 2 6 6 2 1 3
Массив вершин дерева: 1 2 3 4 5 6 7 8 9 10
Минимальная вершина, не содержащаяся в коде Прюфера – это 7
Список ребер: 1 4, 5 7

Третий шаг
Код Прюфера: 1 5 2 6 6 2 1 3
Массив вершин дерева: 1 2 3 4 5 6 7 8 9 10
Минимальная вершина, не содержащаяся в коде Прюфера – это 5
Список ребер: 1 4, 5 7, 2 5

Четвертый шаг
Код Прюфера: 1 5 2 6 6 2 1 3
Массив вершин дерева: 1 2 3 4 56 7 8 9 10
Минимальная вершина, не содержащаяся в коде Прюфера – это 8
Список ребер: 1 4, 5 7, 2 5, 6 8

Пятый шаг
Код Прюфера: 1 5 2 6 6 2 1 3
Массив вершин дерева: 1 2 3 4 56 7 8 9 10
Минимальная вершина, не содержащаяся в коде Прюфера – это 9
Список ребер: 1 4, 5 7, 2 5, 6 8, 6 9

Шестой шаг
Код Прюфера: 1 5 2 6 6 2 1 3
Массив вершин дерева: 1 2 3 4 56 7 8 9 10
Минимальная вершина, не содержащаяся в коде Прюфера – это 6
Список ребер: 1 4, 5 7, 2 5, 6 8, 6 9, 2 6

Седьмой шаг
Код Прюфера: 1 5 2 6 6 2 1 3
Массив вершин дерева: 1 2 3 4 5 6 7 8 9 10
Минимальная вершина, не содержащаяся в коде Прюфера – это 2
Список ребер: 1 4, 5 7, 2 5, 6 8, 6 9, 2 6, 1 2

Восьмой шаг
Код Прюфера: 1 5 2 6 6 2 1 3
Массив вершин дерева: 1 2 3 4 5 6 7 8 9 10
Минимальная вершина, не содержащаяся в коде Прюфера – это 1
Список ребер: 1 4, 5 7, 2 5, 6 8, 6 9, 2 6, 1 2, 3 1

Завершение алгоритма
Код Прюфера: 1 5 2 6 6 2 1 3
Массив вершин дерева: 1 2 3 4 5 6 7 8 9 10
Минимальная вершина, не содержащаяся в коде Прюфера – это 1
Список ребер: 1 4, 5 7, 2 5, 6 8, 6 9, 2 6, 1 2, 3 1, 3 10

Заключение

Код Прюфера был предложен как наглядное и простое доказательство формулы Кэли о числе помеченных деревьев. На практике же его используют чаще для решения комбинаторных задач.

Источники

1. Уилсон Р. Введение в теорию графов. Перевод с англ. М.: Мир, 1977. -208 с.
2. Комбинаторика. Булевы функции. Графы: учеб. пособие / А. А. Балагура, О. В. Кузьмин. – Иркутск: Изд-во ИГУ, 2012. – 115 с.
3. MAXimal [Электронный ресурс] — Режим доступа: ссылка, свободный. (дата обращения: 22.04.2017)

Источник