Построение связного дерева графа

5.2.2. Построение остовного дерева

Граф называется связным, если между любыми двумя его вершинами существует путь. Остовное дерево графа G=(V,E) — это связный граф T=(V,E1) без циклов,в котором E1 — подмножество E.

где T — остовное дерево графа G (G — связный граф),e — произвольно выбранное ребро графа G.

Остовное дерево можно строить так: 1) начать с произвольного ребра графа G; 2) добавлять новые ребра, постоянно следя за тем, чтобы не образовывались циклы; 3) продолжать этот процесс до тех пор, пока не обнаружится, что нельзя присоединить ни одного ребра, поскольку любое новое ребро порождает цикл. Отсутствие цикла обеспечивается так: ребро присоединяется к дереву лишь в том случае, когда одна из его вершин уже содержится в строящемся дереве, а другая пока еще не включена в него.

Основное отношение, используемое в программе,

Здесь Tree — остовное дерево, полученное добавлением множества ребер из G к дереву Tree1.

Пример 3. Построение остовного дерева.

arca(a,b). arca(b,c). arca(c,d). arca(b,d).

expand(Tree1,Tree) :- ap_arca(Tree1,Tree2), expand(Tree2,Tree).

ap_arca(Tree,[arca(A,B)|Tree]) :- arca(A,B), node(A,Tree), not(node(B,Tree));

node(A,Tree) :- member(arca(A,_),Tree); member(arca(_,A),Tree).

5.3. Варианты заданий

1. Определить, является ли связным заданный граф.

2. Найти все вершины графа, к которым существует путь заданной длины от выделенной вершины графа.

3. Найти все вершины графа, достижимые из заданной.

4. Подсчитать количество компонент связности заданного графа.

5. Найти диаметр графа, т.е. максимум расстояний между всевозможными парами его вершин.

6. Найти такую нумерацию вершин орграфа, при которой всякая дуга ведет от вершины с меньшим номером к вершине с большим номером.

7. Дан взвешенный граф. Построить остовное дерево минимальной стоимости.

8. Определить является ли граф гамильтоновым. Найти гамильтонов цикл, т. е. цикл, проходящий через все вершины графа.

9. Задана система односторонних дорог. Найти путь, соединяющий города A и B и не проходящий через заданное множество городов.

10. В заданном графе указать все его четырехвершинные полные подграфы.

11. Известно, что заданный граф — не дерево. Проверить, можно ли удалить из него одну вершину ( вместе с инцидентными ей ребрами), чтобы в результате получилось дерево.

6. Основные стратегии решения задач искусственного интеллекта

6.1.Пространство состояний задачи

Пространством состояний задачи является граф, вершины которого соответствуют ситуациям, встречающимся в задаче (» проблемные ситуации»), а решение задачи сводится к поиску пути в этом графе.

Пространство состояний задачи определяет «правила игры»:

— вершины пространства состояний соответствуют ситуациям;

— дуги соответствуют разрешенным ходам или действиям, или шагам решения задачи.

Конкретная задача определяется: пространством состояний; стартовой вершиной; целевым условием ( т. е. условием, к выполнению которого нужно стремиться).

Целевыми называются вершины, удовлетворяющие целевым условиям.

Каждому разрешенному ходу или действию можно приписать его стоимость. В тех случаях, когда каждый ход имеет стоимость, мы заинтересованы в отыскании решения минимальной стоимости.

Стоимость решения — это сумма стоимостей дуг, из которых состоит решающий путь — путь из стартовой вершины в целевую.

Будем представлять пространство состояний при помощи отношения

которое истинно тогда, когда в пространстве состояний существует разрешенный ход из вершины X в вершину Y. Будем говорить, что Y – это преемник вершины X. Если с ходами связаны их стоимости, мы добавим третий аргумент, стоимость хода C:

Эти отношения можно задавать в программе явным образом при помощи набора соответствующих фактов. Однако, такой принцип непрактичен, поэтому отношение следования after обычно определяется неявно, при помощи правил вычисления вершин преемников некоторой заданной вершины.

Пример 1. Задача манипулирования кубиками.

Проблемная ситуация — список столбиков. Каждый столбик — список кубиков, из которых он составлен. Кубики упорядочены в списке таким образом, что самый верхний кубик находится в голове списка. «Пустые» столбики изображаются как пустые списки.

Отношение следования вытекает из правила:

Ситуация Sit2 — преемник ситуации Sit1, если в Sit1 имеется два столбика Stolb1 и Stolb2 такие, что верхний кубик из Stolb1 можно поставить сверху на Stolb2 и получить тем самым Sit2.

Поскольку все ситуации — списки столбиков, правило транслируется на Пролог так:

— Stolbs — множество столбиков в ситуации Sit1;

— Stolbs1 — множество столбиков без первого столбика;

— Rest — множество столбиков без первого и второго.

Целевое условие в данном примере имеет вид:

Алгоритм поиска программируется как отношение

— Start — стартовая вершина пространства состояний,

— Solution — путь, ведущий из вершины Start в любую целевую вершину.

Для конкретного примера обращение к Пролог- системе имеет вид:

Список Solution представляет собой план преобразования исходного состояния в состояние, в котором три кубика поставлены друг на друга в указанном порядке : [a,b,c].

Источник

8. Деревья.

Деревом называют связный неориентированный граф без циклов. Иначе, связный граф, содержащий N вершин и N-1 ребер.

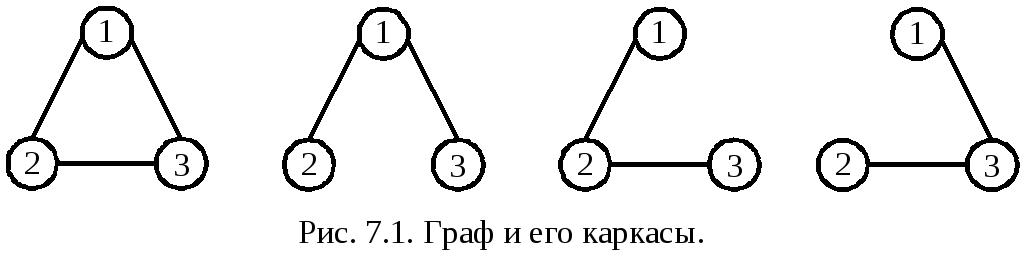
Для связного неориентированного графа G = V, E > каждое дерево V, T > , где TE называют стягивающим деревом (каркасом, остовом). Число различных каркасов полного связного неориентированного графа с N вершинами равно N N -2 (Кэли)(рис. 7.1).

Рассмотрим два алгоритма нахождения каркаса (одного), основанных на методах просмотра графа поиском в глубину и в ширину.

7.1. Выделение дерева методом поиска в глубину и в ширину.

Известно, что как при поиске в глубину, так и при поиске в ширину просматриваются все вершины связного графа. Использование множества Т обеспечивает «подключение» очередного ребра к каркасу без образования циклов. Действительно, цикл образуется, если мы соединим две просмотренные вершины. Но в нашем случае «подключается» ребро, соединяющее просмотренную вершину с непросмотренной. И, наконец, по самой логике методов поиска в глубину и в ширину мы строим связный граф.

Для хранения ребер, образующих каркас, будем использовать структуру данных :

вершины, инцидентные ребру j>

Построение остовного дерева (каркаса) методом поиска в глубину.

Procedure Tree_Gl ( v :Integer );

Читайте также:  Kudo герметик для дерева

For j := 1 To n Do

If ( A [v, j] <> 0 ) And Not ( T In [ j ] )

Вызов: … s:=1; z:=0; T:=[ ]; Tree_Gl(s); Вывод матрицы B; …

Построение остовного дерева (каркаса) методом поиска в ширину.

For j := 1 To n Do

If (A[ v, j ] <> 0 ) And Not ( j In T ) записываем в очередь >

Then Begin Inc( w ); Q[ w ] := j; T := T + [ j ];

Inc( z ); B[ 1, z ] :=v; B[ 2, z ] := j;

Вызов: … s:=1; z :=0; SH_Obhod ( s ); Вывод матрицы B; …

Порождение всех каркасов графа

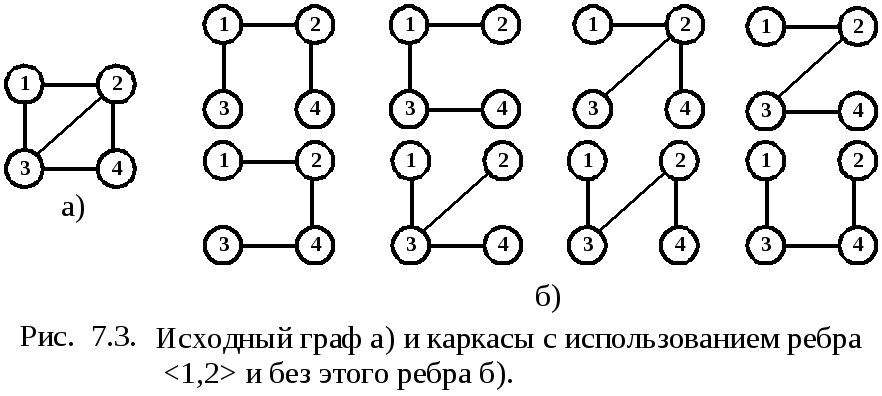
Для порождения очередного каркаса ранее построенные не привлекаются, используется только последний. Множество всех каркасов делится на два класс: содержащие выделенное ребро v, u > и не содержащие его. Каркасы последовательно строятся в графах G _{v, u >} и G — v, u >. Каждый из графов G _{v, u >} и G — v, u > меньше, чем G. Последовательное применение этого шага уменьшает графы до тех пор, пока не будет построен очередной каркас либо графы станут несвязными и не имеющими каркасов. Пример графа и его каркасов в той последовательности, в которой они порождаются данным методом, приведен на рис 7.3.

Q :Array [1..nq] Of Integer; очередь>

B :Array [1..2,1..n] Of Integer;

v – номер вершины, из которой выходит ребро;

u – номер вершины, начиная с которой следует искать очередное

k – число ребер в каждом каркасе.

Var j :Integer; (рекурсивный алгоритм)>

If r >= w Then Exit;

If (A[ v, j ] <> 0 ) And Not ( j In T ) Then Begin есть ребро < v ,j >,

T := T + [ j ]; причем вершина j еще не просмотрена

Inc( z ); B [ 1, z ] := v; B [ 2, z ] := j; включаем это ребро в каркас

Q[ w ] := j; Inc( w ); а вершину j в очередь

Ostov ( v, j+1 ); и едем вперед>

If z = k Then Begin WriteOstov( B, k ); Exit; End;

If j = n + 1 Then

Ostov( Q[ r ], 1 ); переходим к следующей вершине из очереди и

Dec( r ); так до тех пор, пока не будет построен каркас>

Begin … Q[1]:=1; r:=1; w:=2; z:=0; k:=3; T :=[1]; Ostov(1,2); … End;

Источник