2 Таблица идентификаторов
Требуется написать программу, которая получает на входе набор идентификаторов, организует таблицу по заданному методу и позволяет осуществить многократный поиск идентификатора в этой таблице. Список идентификаторов считать заданным в виде текстового файла.
Выданному варианту задания соответствует построение таблицы идентификаторов по методу цепочек. Для сравнения кроме предложенного метода реализуем построение таблицы идентификаторов по методу бинарного дерева. Для большей эффективности второй метод будет являться комбинированным.
2.2 Назначение таблиц идентификаторов
Проверка правильности семантики и генерация кода требуют знания характеристик идентификаторов, используемых в программе на исходном языке. Эти характеристики выясняются из описаний и из того, как идентификаторы используются в программе и накапливаются в таблице символов или таблице идентификаторов. Любая таблица символов состоит из набора полей, количество которых равно числу идентификаторов программы. Каждое поле содержит в себе полную информацию о данном элементе таблицы. Под идентификаторами подразумеваются константы, переменные, имена процедур и функций, формальные и фактические параметры.
В нашей курсовой работе таблица идентификаторов будет применяться для хранения информации об используемых переменных, а также в разделе 5 «Генерация и оптимизация ассемблерного кода» при распределении регистров микропроцессора между переменными.
2.3 Метод цепочек
Метод цепочек работает по следующему алгоритму:
Шаг 1. Во все ячейки хеш-таблицы поместить пустое значение, таблица идентификаторов пуста, переменная FreePtr (указатель первой свободной ячейки) указывает на начало таблицы идентификаторов; i:=1.
Шаг 2. Вычислить значение хеш-функции ni для нового элемента Ai. Если ячейка хеш-таблицы по адресу ni пустая, то поместить в нее значение переменной FreePtr и перейти к шагу 5; иначе перейти к шагу 3.
Шаг 3. Положить j:=1, выбрать из хеш-таблицы адрес ячейки таблицы идентификаторов mj и перейти к шагу 4.
Шаг 4. Для ячейки таблицы идентификаторов по адресу mj проверить значение поля ссылки. Если оно пустое, то записать в него адрес из переменной FreePtr и перейти к шагу 5; иначе j:=j+1, выбрать из поля ссылки адрес mj и повторить шаг 4.
Шаг 5. Добавить в таблицу идентификаторов новую ячейку, записать в нее информацию для элемента Ai (поле ссылки должно быть пустым), в переменную FreePtr поместить адрес за концом добавленной ячейки. Если больше нет идентификаторов, которые надо разместить в таблице, то выполнение алгоритма закончено, иначе i:=i+1 и перейти к шагу 2.
В разрабатываемой программе метод цепочек реализует модуль ChainFunc. Для реализации был использован алгоритм, представленный в методических указаниях. Результаты заполнения и поиска в таблице идентификаторов выводятся в главном окне программы.
2.4 Метод бинарного дерева
Каждый узел дерева представляет собой элемент таблицы, причем корневой узел является первым элементом. При построении дерева элементы сравниваются между собой, и в зависимости от результатов, выбирается путь в дереве.
Алгоритм построения таблицы идентификаторов методом бинарного дерева можно представить следующим образом:
Шаг 1. Считать первый элемент во входном списке, создать корневой узел, поместить в него первый элемент и перейти к шагу 4.
Шаг 2. Если текущий узел пуст, заносим в него значение поступившего на вход элемента и переходим к шагу 4.. Иначе переходим к шагу 3.
Шаг 3. Если значение в текущем узле совпадает с поступившим на вход элементом, данный элемент уже есть в таблице идентификаторов, перейти к шагу 4. Иначе сравнить элемент со значением в текущем узле. Если это значение меньше значения, хранимого в текущем узле, сделать текущим левый дочерний узел текущего узла и перейти к шагу 2. Иначе сделать текущим правый дочерний узел и перейти к шагу 2.
Шаг 4. Если больше нет идентификаторов, которые надо разместить в таблице, то выполнение алгоритма закончено, иначе считать следующий идентификатор и перейти к шагу 2.
В разрабатываемой программе комбинированный метод бинарного дерева реализуется в модуле BinTree. Иллюстрация структуры полученной таблицы идентификаторов приводится в видет отдельного диалогового окна, реализованного в модуле TreeDialog.
Источник
Построение таблиц идентификаторов по методу бинарного дерева.
Можно сократить время поиска искомого элемента в таблице идентификаторов, не увеличивая значительно время, необходимое на ее заполнение. Для этого надо отказаться от организации таблицы в виде непрерывного массива данных.
Существует метод построения таблиц, при котором таблица имеет форму бинарного дерева. Каждый узел дерева представляет собой элемент таблицы, причем корневой узел является первым элементом, встреченным при заполнении таблицы. Дерево называется бинарным, так как каждая вершина в нем может иметь не более двух ветвей (и, следовательно, не более двух нижележащих вершин). Для определенности будем называть две ветви «правая» и «левая».
Будем считать, что алгоритм заполнения бинарного дерева работает с потоком входных данных, содержащим идентификаторы (в компиляторе этот поток данных порождается в процессе разбора текста исходной программы). Первый идентификатор, как уже было сказано, помещается в вершину дерева. Все дальнейшие идентификаторы попадают в дерево по следующему алгоритму.
Шаг 1. Выбрать очередной идентификатор из входного потока данных. Если очередного идентификатора нет, то построение дерева закончено.
Шаг 2. Сделать текущим узлом дерева корневую вершину.
Шаг 3. Сравнить очередной идентификатор с идентификатором, содержащемся в текущем узле дерева.
Шаг 4. Если очередной идентификатор меньше, то перейти к шагу 5, если равен — сообщить об ошибке и прекратить выполнение алгоритма (двух одинаковых идентификаторов быть не должно!), иначе — перейти к шагу 7.
Шаг 5. Если у текущего узла существует левая вершина, то сделать ее текущим узлом и вернуться к шагу 3, иначе — перейти к шагу 6.
Шаг 6. Создать новую вершину, поместить в нее очередной идентификатор, сделать эту новую вершину левой вершиной текущего узла и вернуться к шагу 1.
Шаг 7. Если у текущего узла существует правая вершина, то сделать ее текущим узлом и вернуться к шагу 3, иначе — перейти к шагу 8.
Шаг 8. Создать новую вершину, поместить в нее очередной идентификатор, сделать эту новую вершину правой вершиной текущего узла и вернуться к шагу 1.
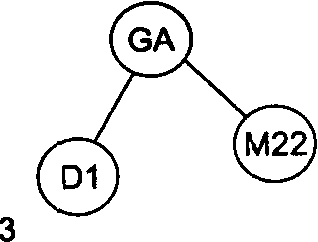
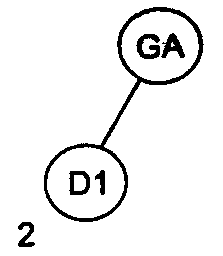
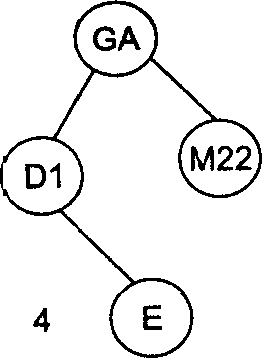
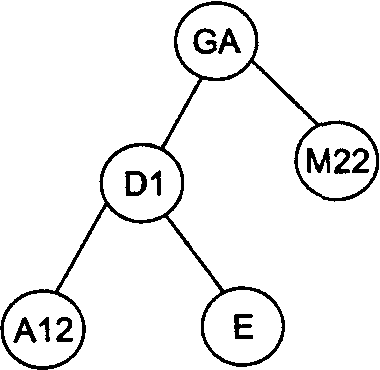
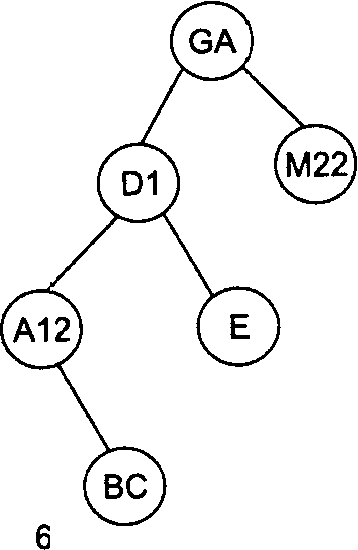
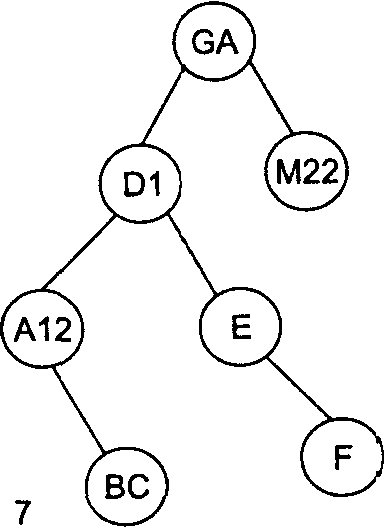
Рассмотрим в качестве примера последовательность идентификаторов GA, Dl, M22, Е, А12, ВС, F. На рис. 1 проиллюстрирован весь процесс построения бинарного дерева для этой последовательности идентификаторов.
Поиск нужного элемента в дереве выполняется по алгоритму, схожему с алгоритмом заполнения дерева.
Рис 1. Пошаговое заполнение бинарного дерева для последовательности идентификаторов GA, D1, M22, Е, А12, ВС, F
1. Выбрать очередной идентификатор из входного потока данных. Если очередного идентификатора нет, то построение дерева закончено.
2. Сделать текущим узлом дерева корневую вершину.
3. Сравнить имя очередного идентификатора с именем идентификатора, содержащегося в текущем узле дерева.
4. Если имя очередного идентификатора меньше, то перейти к шагу 5, если равно — прекратить выполнение алгоритма (двух одинаковых идентификаторов быть не должно!), иначе—перейти к шагу 7.
5. Если у текущего узла существует левая вершина, то сделать ее текущим узлом и вернуться к шагу 3, иначе — перейти к шагу 6.
6. Создать новую вершину, поместить в нее информацию об о черепном идентификатор е, сделать эту новую вершину левой вершиной текущего узла и вернуться к шагу 1.
7. Если у текущего узла существует правая вершина, то сделать ее текущим узлом и вернуться к шагу 3, иначе—перейти к шагу 8.
8. Создать новую вершину, поместить в нее информацию об очередном идентификаторе, сделать эту новую вершину правой вершиной текущего узла и вернуться к шагу 1.
Например, произведем поиск в дереве, изображенном на рис.1 (7), идентификатора А12. Берем корневую вершину (она становится текущим узлом), сравниваем идентификаторы GA и А12. Искомый идентификатор меньше — текущим узлом становится левая вершина D1. Опять сравниваем идентификаторы. Искомый идентификатор меньше — текущим узлом становится левая вершина А12. При следующем сравнении искомый идентификатор найден.
Если искать отсутствующий идентификатор — например, A11, — то поиск опять пойдет от корневой вершины. Сравниваем идентификаторы GA и АН. Искомый идентификатор меньше — текущим узлом становится левая вершина D1. Опять сравниваем идентификаторы. Искомый идентификатор меньше — текущим узлом становится левая вершина А12. Искомый идентификатор меньше, но левая вершина у узла А12 отсутствует, поэтому в данном случае искомый идентификатор не найден.
Для данного метода число требуемых сравнений и форма получившегося дерева во многом зависят от того порядка, в котором поступают идентификаторы. Например, если в рассмотренном выше примере вместо последовательности идентификаторов GA, 01, M22, E, A12, ВС, F взять последовательность А12, GA, D1, (22, E, ВС, F, то полученное дерево будет иметь иной вид. А если в качестве примера взять последовательность идентификаторов А, В, С, D, E, F, то дерево выродится в упорядоченный однонаправленный связный список. Эта особенность является недостатком данного метода организации таблиц идентификаторов. Другим недостатком является необходимость работы с динамическим выделением памяти при построении дерева.
Если предположить, что последовательность идентификаторов в исходной программе является статистически неупорядоченной (что в целом соответствует действительности), то можно считать, что построенное бинарное дерево будет невырожденным. Тогда среднее время на заполнение дерева (ТД) и на поиск элемента в нем (ТП) можно оценить следующим образом:
В целом метод бинарного дерева является довольно удачным механизмом для организации таблиц идентификаторов. Он нашел свое применение в ряде компиляторов. Иногда компиляторы строят несколько различных деревьев для идентификаторов разных типов и разной длины.
Источник