Построить дерево кратчайших путей

§7. Задача о кратчайшем пути на графе. Алгоритм Дейкстры

Напомним, что сетью называется пара N=(G,α), где G – орграф, а α – функция из множества вершин графа в множество действительных чисел. Другими словами, каждой дуге графа поставлено в соответствие некоторое неотрицательное число, которое в данном случае называется длиной дуги. Введем длину пути как сумму длин дуг, составляющих путь. Расстоянием d(u,v) от вершины u до вершины v называется длина кратчайшего пути из u в v. Если нет ни одного пути из u в v, то считают d(u,v)=∞. Расстояние от u до u равно нулю.

Для сети N возникает задача нахождения расстояния d(u,v) для данных вершин u и v и соответствующего кратчайшего пути. Известно несколько способов решения этой задачи. Мы рассмотрим один из них, основой которого является алгоритм Дейкстры. Он вычисляет расстояние от фиксированной вершины v₀ до всех остальных вершин сети.

Прежде, чем привести описание алгоритма, введем необходимые обозначения. Пусть N=(G,α) – сеть, v₀ – фиксированная вершина этой сети, v₁,…,v_m – остальные вершины. На множестве пар вершин (u,v) введем функцию L(u,v) следующим образом:

L(u,v)=

α(e), если e – дуга с началом в u и концом в v,

∞ – если такой дуги не существует.

В описании алгоритма участвует еще некоторое подмножество S множества V вершин графа. В ходе выполнения алгоритма вершины последовательно исключают из S, до тех пор, пока не останется ни одной, и вычисляют величины d(v_i), равные кратчайшему пути из v₀ в v_i , не содержащему вершин из S. Алгоритм также имеет графическую реализацию, в которой множеству S соответствуют неокрашенные вершины, а окрашивание – это исключение вершины из S. Итак, дадим формальное описание алгоритма Дейкстры.

Шаг 1. (инициализация). Положить S:=V\v₀> (то есть окрасить вершину v₀), d(v_i)=∞ для всех i=1,…,m, положить y= v₀.

Шаг 2. Для всех vS (т.е. для всех неокрашенных вершин) пересчитать d(v) по формуле: d(v) =min< d(v), d(y)+L(y,v)> . Если все d(v)= ∞, перейти к шагу 5 (это означает, что в графе отсутствуют пути из v₀ в неокрашенные вершины).

Шаг 3. Выбрать в S вершину w, для которой величина d(v) минимальна, и положить S:=S\w>, т.е. окрасить вершину w. Окрасить дугу, ведущую в вершину w из вершины, которая была взята в качестве y последний раз, когда в менялось значение d для вершины w . Положить y= w. Если S не пусто, перейти к шагу 2, иначе к шагу 4.

Шаг 4. Конец работы алгоритма.

При графической реализации алгоритма для графа будет построено покрывающее дерево с корнем в вершине v₀ (если оно существует). Если требуется определить не сам кратчайший путь, а лишь его длину, то можно не проводить окрашивание, а только вычислять на каждой итерации множество S . Расчет условно оформлять в виде таблице, как показано в следующем примере.

Пример 1. Для графа, изображенного на рис. 37, найти расстояния от вершины v₀ до остальных вершин и построить дерево кратчайших путей с корнем в v₀ .

Работа алгоритма будет иллюстрироваться заполнением приведенной ниже таблицы. Кроме того, для каждой строки таблицы приводится рисунок, соответствующий графической реализации алгоритма; на этом рисунке окрашенные вершины изображаются черным кружком, окрашенные ребра выделены жирными линиями.

Источник

Задача 2: Задача о нахождении дерева кратчайших расстояний – нахождение кратчайшего пути из одной вершины в любую другую.

Пусть дан ориентированный связный граф со взвешенными ребрами. Вес ребра (x_i,x_j) обозначим c_ij.

Требуется найти в заданном графе путь, соединяющий две заданные вершины и доставляющий минимум или максимум суммарного веса входящих в него рёбер. Чаще всего эта функция трактуется как длина пути, и задача называется задачей о кратчайших путях.

Для решения этой задачи применяется алгоритм Дейкстры (Голландия, 1930-2002), реализующий принцип динамического программирования: сведение данной задачи к аналогичной, имеющей меньшую размерность так, чтобы её решение являлось частью решения большей задачи.

Суть алгоритма: начиная с исходной вершины (вес = 0), добавлять к пути по одной вершины, определяя её вес (метку) как расстояние до неё от исходной вершины через уже добавленные, возможно, меняя их вес.

После обработки всех вершин путь строится от конечной вершины по рёбрам, дающим соответствующий вес.

Описание алгоритма Дейкстры (минимальный путь):

Шаг 0. Устанавливаем для исходной вершины x₁ постоянный вес w₁=0. Всем остальным вершинам присваивается временный вес ∞.

Шаг 1. Вершина, имеющая меньший вес называется «ближайшей». Среди дуг, исходящих из ближайшей вершины выбираем дугу (x_i,x_j), имеющую меньший вес. Новый вес конечной её вершины x_j вычисляем как минимум из имеющегося её веса w_j и суммы w_i+ c_i,j. Повторяем эту операцию для остальных дуг ближайшей вершины.

Шаг 2. Когда все дуги ближайшей вершины проверены, текущий вес её становится постоянным и она (и исходящие из неё дуги) вычёркиваются из рассмотрения. Если остались невычеркнутые вершины, переходим к шагу 1.

Шаг 3. От конечной вершины по очереди строится обратный путь к исходной вершине против направления дуг. От текущей вершины выбирается та предшествующая, вес которой меньше веса данной вершины на вес соединяющей их дуги. В итоге путь придёт в исходную вершину x₁ с весом w₁=0.

Пример: Найти минимальный путь из вершины 1 в вершину 5.

Все вершины рассмотрены. Фактически найдены кратчайшие расстояния от вершины 1 до всех вершин графа.

Найдём путь до вершины 5. Её вес 20.

Предыдущая вершина 6. Её вес 11=20-9.

Перед ней вершина 3. Её вес 9=11-2.

Перед ней вершина 1. Её вес 0=9-9.

Это исходная вершина. Задача решена.

Ответ: кратчайший путь 1 – 3 – 6 – 5. Длина пути 20.

Алгоритм Дейкстры

(в случае неотрицательных весов.)

Дано: непyстой взвешенный гpаф G=(V,E) с неотрицательными весами дуг. Требуется найти кpатчайший пyть от s к t (s≠t).

Для данного взвешенного графа алгоритм дает кратчайшее расстояние от вершины V₁ к вершине V_n.

Каждой вершине поставим в соответствие упорядоченную пару (∞,0). Первая координата вершины V_i(m,v_r) будет означать присвоенное расстояние от вершины V₁ к вершине V_i, а вторая координата — предыдущую вершину пути от V₁ к V_i.

1) Начать в вершине V₁(∞,0), заменить ее на V₁(0,0) и сделать постоянной. Остальные вершины на этот момент оставить временными.

2) Когда вершина V_k (m,v_r) станет постоянной, для каждой вершины V_j, смежной к V_k, прибавить величину m к расстоянию от вершины V_k к вершине V_j. Если это значение меньше, чем текущее расстояние, присвоенное вершине V_j, заменить текущее расстояние этой суммой и заменить вторую координату на V_k.

3) Найти минимум из расстояний, приписанных временным вершинам. Первую из вершин с таким расстоянием делаем постоянной.

4) Если V_n — не постоянная вершина, то возвращаемся к пункту 2).

5) Если V_n — постоянная вершина, то расстояние, присвоенное вершине V_n является кратчайшим расстоянием от V₁ к V_n.

6) Для нахождения пути начать в вершине V_n найти предшествующую ей вершину пути (вторая координата). Для каждой вершины пути V_j находить предшествующую ей вершину пути, пока не будет достигнута вершина V₁. Перестановка вершин в обратном порядке даст кратчайший путь.

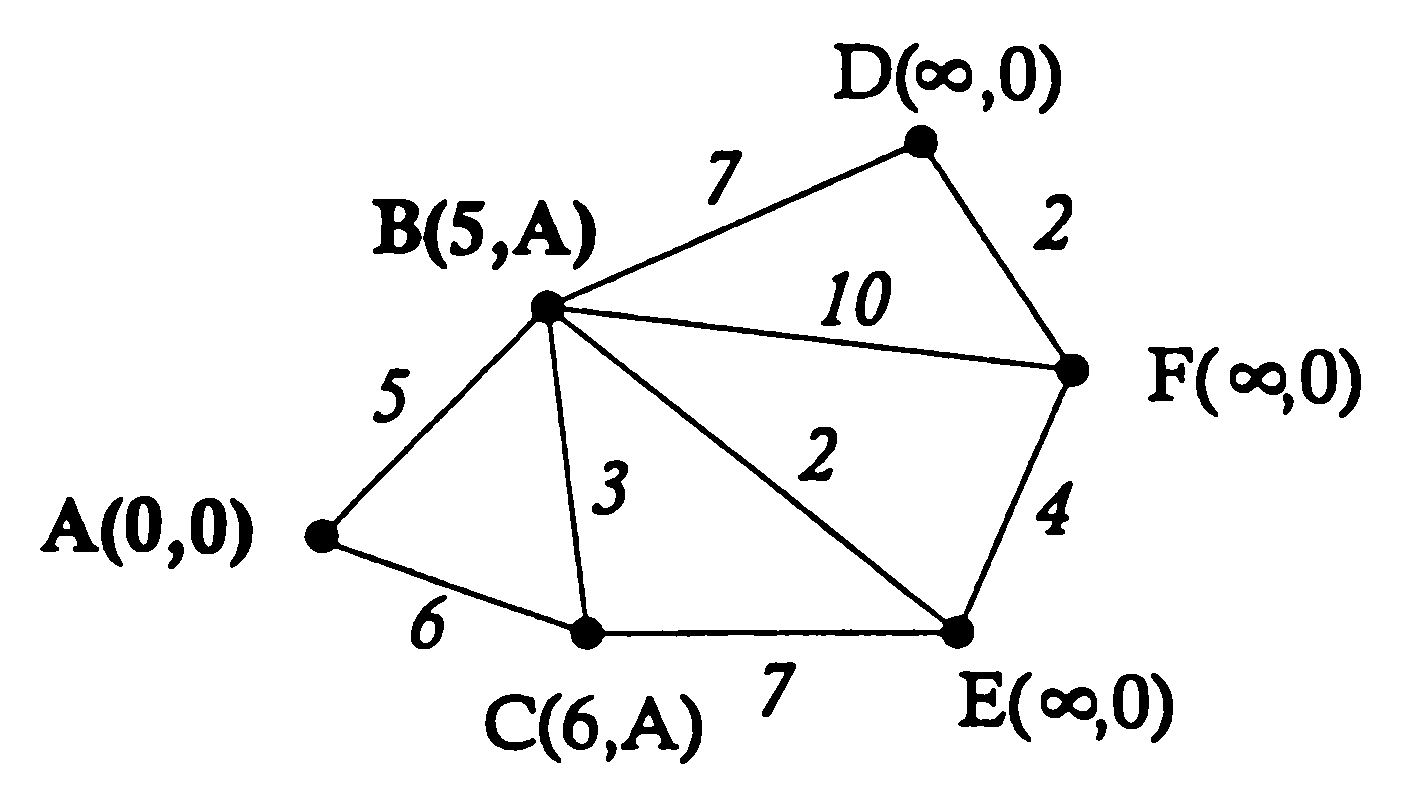
ПРИМЕР. Пусть взвешенный граф, в котором отыскивается кратчайшее расстояние от вершины А к вершине F.

Поставив в соответствие каждой вершине упорядоченную пару (∞,0), рассматриваемый граф приводим к виду.

Приступим к построению путей от вершины А к другим вершинам.

Первая компонента упорядоченной пары покажет длину кратчайшего пути к вершине в момент достижения, а вторая — укажет на предыдущую вершину кратчайшего пути. Первая компонента будет содержать ∞, а вторая — 0 до тех пор, пока путь не найден.

Шаг1. Вершина, которая стала постоянной, будет выделена жирным шрифтом. Выполнив шаг 1 алгоритма, получаем граф

Шаг 2. Поскольку вершины В и С — смежные с вершиной А, выполняем шаг 2 и упорядоченной паре для вершины В присваиваем значение B(5, А), а упорядоченной паре для вершины С присваиваем значение C(6,А).

Шаг 3. Выполнив шаг 3, выбираем наименьшее из временных присвоенных значений. В данном случае это расстояние до вершины А, равное 5, и вершину В(5, А) делаем постоянной. Таким образом, получаем.

Возвращаясь к шагу 2, рассмотрим временные вершины С, D, Е и F, смежные с вершиной В. В каждом случае прибавляем расстояние от вершины А к вершине В к расстоянию от вершины В к данным вершинам.

Таким образом, для вершины С это будет 5 + 3 = 8. Для вершины D имеем 5 + 7 = 12. Для вершины Е имеем 5 + 2 = 7. Для вершины F получаем 5 + 10 = 15.

Поскольку новое расстояние до вершины С не меньше, чем уже присвоенное, упорядоченную пару С(6,А) оставляем без изменения. Новые расстояния до вершин Д Е и F меньше уже присвоенных, поэтому им задаем значения, которые получены для пути из вершины В, т.е. меняем их на D(12, В), Е(7,В) и F(15,В).

Выполнив шаг 3, находим наименьшее из расстояний, присвоенных временным вершинам, поэтому берем min = 6, и поскольку вершина С имеет это расстояние, делаем вершину С(6, А) постоянной. Таким образом, получаем.

Теперь берем новую постоянную вершину С. Выполнение шага 2 не приводит к изменениям. Выполнив шаг 3, делаем вершину Е(7,В) постоянной. Получаем

Берем новую постоянную вершину Е и, используя шаг 2, меняем F(15, В) на F(11,E). Выполнив шаг 3, делаем вершину F(11,E) постоянной. Таким образом, получаем.

Вершина F стала постоянной, поэтому процесс завершен и 11 — это кратчайшее расстояние от вершины А к вершине F.

Если бы совокупность вершин, смежных с постоянной вершиной, была исчерпана до того, как мы достигли вершину F, то задача не имела бы решения, поскольку не было бы пути от вершины А к вершине F.

Для нахождения кратчайшего пути заметим, что вершине F предшествует вершина Е, вершине Е предшествует вершина В, а вершине В предшествует вершина А. Поэтому кратчайшим путем является ABEF.

Алгоритм Дейкстры не всегда находит правильное решение в случае произвольных весов ребер (дуг) графа.

алгоритм Дейкстры найдет маршрут s(s,t)t длины 1 между вершинами s и t, а не минимальный маршрут длины 2+(-2)=0, проходящий через третью вершину графа.

Задача 3: Построение матрицы кратчайших расстояний – нахождение кратчайших путей для любой пары вершин.

Пусть дан ориентированный связный граф со взвешенными ребрами. Вес ребра (x_i,x_j) обозначим c_ij или C[i, j].

Требуется для каждой упорядоченной пары вершин v, w найти любой путь от вершины v в вершины w, длина которого минимальна среди всех возможных путей от v к w.

Пример прикладной задачи3:

Телефонная компания обслуживает пять удалённых друг от друга районов, которые связаны следующей сетью

Компании необходимо определить наиболее эффективные маршруты пересылки сообщений между районами.

Для определенности положим, что вершины графа последовательно пронумерованы от 1 до n. Алгоритм Флойда использует матрицу А размера nn, в которой вычисляются длины кратчайших путей.

Вначале A₀[i, j] = C[i, j] для всех i  j. Если дуга i  j отсутствует, то C[i, j] = ∞. Каждый диагональный элемент матрицы А равен 0.

Над матрицей А выполняется n – 1 итераций. После k-й итерации A[i, j] содержит значение наименьшей длины путей из вершины i в вершину j, которые не проходят через вершины с номером, большим k. Другими словами, между концевыми вершинами пути i и j могут находиться только вершины, номера которых меньше или равны k.

На k-й итерации для вычисления матрицы А применяется следующая формула:

Для вычисления A_k[i, j] проводится сравнение величины A_k-1[i, j] (т.е. стоимость пути от вершины i к вершине j без участия вершины k или другой вершины с более высоким номером) с величиной A_k-1[i, k] + A_k-1[k, j] (стоимость пути от вершины i до вершины k плюс стоимость пути от вершины k до вершины j).

Если путь через вершину k дешевле, чем A_k-1[i, j], то величина A_k[i, j] изменяется.

Пример. Найти матрицу кратчайших расстояний для графа.

Источник