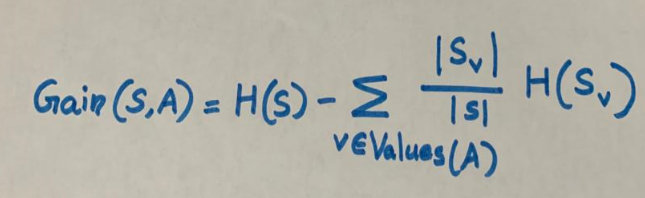Построить дерево принятия решений

Как разобраться в дереве принятия решений и сделать его на Python

Совсем скоро, 20 ноября, у нас стартует новый поток «Математика и Machine Learning для Data Science», и в преддверии этого мы делимся с вами полезным переводом с подробным, иллюстрированным объяснением дерева решений, разъяснением энтропии дерева решений с формулами и простыми примерами, вводом понятия «информационный выигрыш», которое игнорируется большинством умозрительно-простых туториалов. Статья рассчитана на любящих математику новичков, которые хотят больше разобраться в работе дерева принятия решений. Для полной ясности взят совсем маленький набор данных. В конце статьи — ссылка на код на Github.

Дерево решений — тип контролируемого машинного обучения, который в основном используется в задачах классификации. Дерево решений само по себе — это в основном жадное, нисходящее, рекурсивное разбиение. «Жадное», потому что на каждом шагу выбирается лучшее разбиение. «Сверху вниз» — потому что мы начинаем с корневого узла, который содержит все записи, а затем делается разбиение.

Корневой узел — самый верхний узел в дереве решений называется корневой узел.
Узел принятия решения — подузел, который разделяется на дополнительные подузлы, известен как узел принятия решения.

Лист/терминальный узел — узел, который не разделяется на другие узлы, называется терминальный узел, или лист.

Набор данных

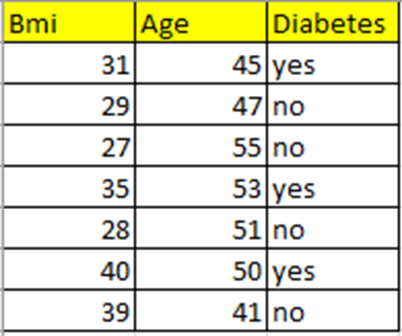
Я взяла совсем маленький набор данных, содержащий индекс массы тела (BMI), возраст (Age) и целевую переменную Diabetes (диабет). Давайте спрогнозируем, будет у человека данного возраста и индекса массы тела диабет или нет.

Представление набора данных

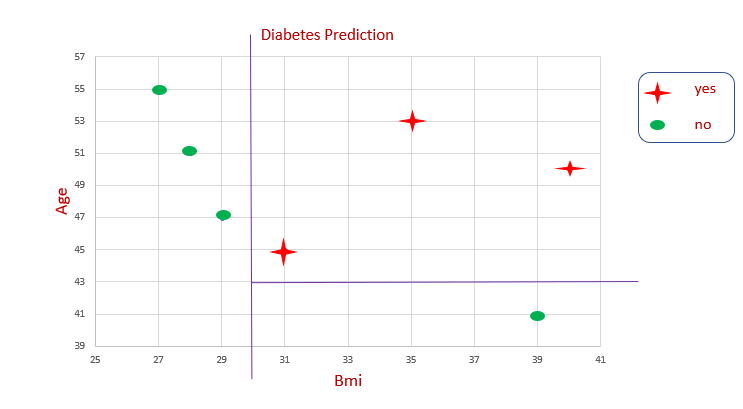
На графике невозможно провести какую-то прямую, чтобы определить границу принятия решения. Снова и снова мы разделяем данные, чтобы получить границу решения. Так работает алгоритм дерева решений.

Вот так в дереве решений происходит разбиение.

Важные теоретические определения

Энтропия

Энтропия — это мера случайности или неопределенности. Уровень энтропии колеблется от 0 до 1 . Когда энтропия равна 0, это означает, что подмножество чистое, то есть в нем нет случайных элементов. Когда энтропия равна 1, это означает высокую степень случайности. Энтропия обозначается символами H(S).

Формула энтропии

Энтропия вычисляется так: -(p(0) * log(P(0)) + p(1) * log(P(1)))

Связь между энтропией и вероятностью

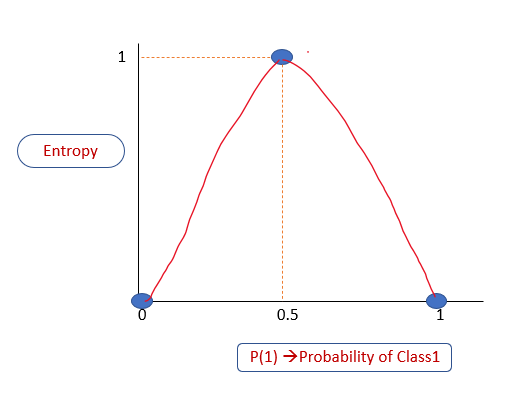
Когда энтропия равна 0, это означает, что подмножество «чистое», то есть в нем нет энтропии: либо все «да», либо все голоса «нет». Когда она равна 1, то это означает высокую степень случайности. Построим график вероятности P(1) вероятности принадлежности к классу 1 в зависимости от энтропии. Из объяснения выше мы знаем, что:

Если P(1) равно 0, то энтропия равна 0
Если P(1) равно 1, то энтропия равна 0
Если P(1) равно 0,5, то энтропия равна 1

Уровень энтропии всегда находится в диапазоне от 0 до 1.

Информационный выигрыш

Информационный выигрыш для разбиения рассчитывается путем вычитания взвешенных энтропий каждой ветви из исходной энтропии. Используем его для принятия решения о порядке расположения атрибутов в узлах дерева решений.

Как работает дерево решений

В нашем наборе данных два атрибута, BMI и Age. В базе данных семь записей. Построим дерево решений для нашего набора данных.

1. Корневой узел

В дереве решений начнем с корневого узла. Возьмем все записи (в нашем наборе данных их семь) в качестве обучающих выборок.

В корневом узле наблюдаем три голоса за и четыре против.
Вероятность принадлежности к классу 0 равна 4/7. Четыре из семи записей принадлежат к классу 0.
P(0) = 4/7
Вероятность принадлежности к классу 1 равна 3/7. То есть три из семи записей принадлежат классу 1.
P(1) = 3/7.

Вычисляем энтропию корневого узла:

2. Как происходит разбиение?

У нас есть два атрибута — BMI и Age. Как на основе этих атрибутов происходит разбиение? Как проверить эффективность разбиения?

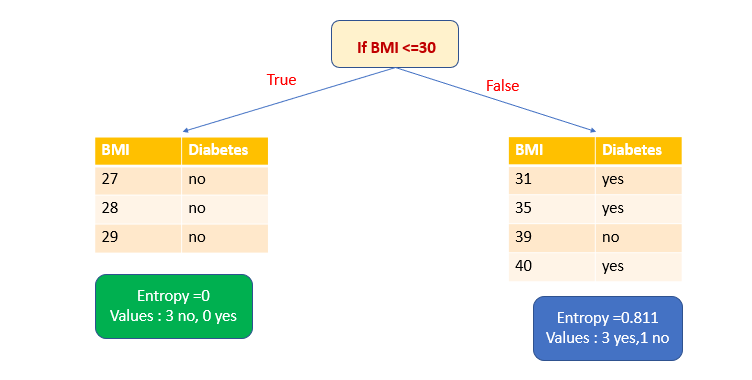
1. При выборе атрибута BMI в качестве переменной разделения и ≤30 в качестве точки разделения мы получим одно чистое подмножество.

Точки разбиения рассматриваются для каждой точки набора данных. Таким образом, если точки данных уникальны, то для n точек данных будет n-1 точек разбиения. То есть в зависимости от выбранных точки и переменной разбиения мы получаем высокий информационный выигрыш и выбираем разделение с этим выигрышем. В большом наборе данных принято считать только точки разделения при определенных процентах распределения значений: 10, 20, 30%. У нас набор данных небольшой, поэтому, видя все точки разделения данных, я выбрала в качестве точки разделения значения ≤30.

Энтропия чистого подмножества равна нулю. Теперь рассчитаем энтропию другого подмножества. Здесь у нас три голоса за и один против.

Чтобы решить, какой атрибут выбрать для разбиения, нужно вычислить информационный выигрыш.

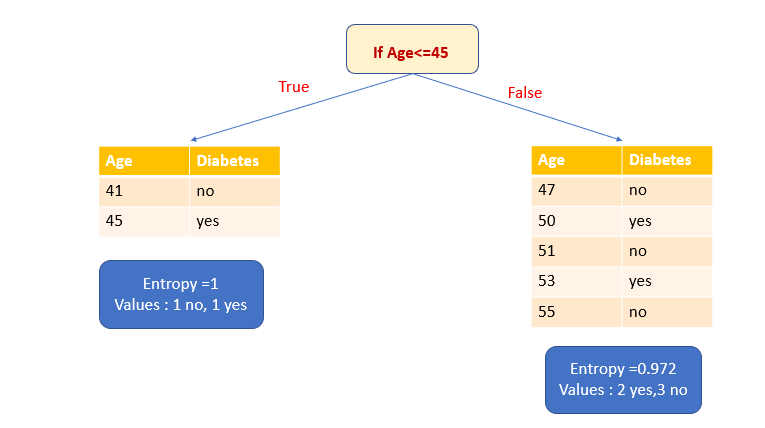
2. Выберем атрибут Age в качестве переменной разбиения и ≤45 в качестве точки разбиения.

Давайте сначала вычислим энтропию подмножества True. У него есть одно да и одно нет. Это высокий уровень неопределенности. Энтропия равна 1. Теперь рассчитаем энтропию подмножества False. В нем два голоса за и три против.

3. Рассчитаем информационный выигрыш.

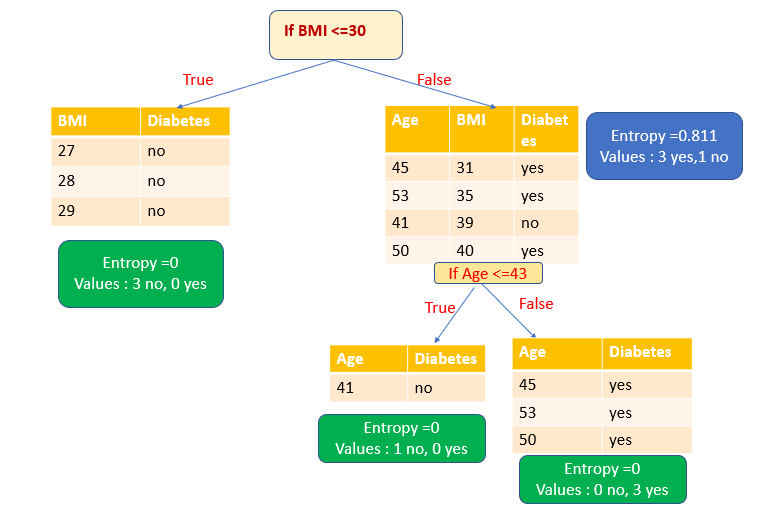
Мы должны выбрать атрибут, имеющий высокий информационный выигрыш. В нашем примере такую ценность имеет только атрибут BMI. Таким образом, атрибут BMI выбирается в качестве переменной разбиения. После разбиения по атрибуту BMI мы получаем одно чистое подмножество (листовой узел) и одно нечистое подмножество. Снова разделим это нечистое подмножество на основе атрибута Age. Теперь у нас есть два чистых подмножества (листовой узел).

Итак, мы создали дерево решений с чистыми подмножествами.

Напишем это на Python с помощью sklearn

1. Импортируем библиотеки.

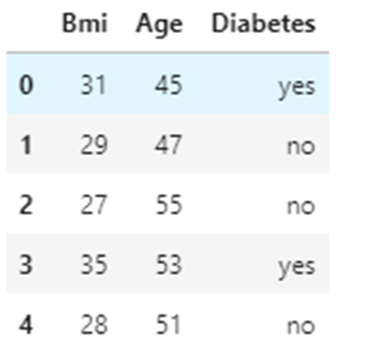
import numpy as np import pandas as pd import matplotlib.pyplot as plt import seaborn as sns 

2. Загрузим данные.

df=pd.read_csv("Diabetes1.csv") df.head() 

3. Разделим переменные на x и y.

Атрибуты BMI и Age принимаются за x.
Атрибут Diabetes (целевая переменная) принимается за y.

x=df.iloc[. 2] y=df.iloc[:,2:] x.head(3) 

4. Построим модель с помощью sklearn

from sklearn import tree model=tree.DecisionTreeClassifier(criterion="entropy") model.fit(x,y) 

Вывод: DecisionTreeClassifier (criterion=«entropy»)

5. Оценка модели

Вывод: 1.0 . Мы взяли очень маленький набор данных, поэтому оценка равна 1.

6. Прогнозирование с помощью модели

Давайте предскажем, будет ли диабет у человека 47 лет с ИМТ 29. Напомню, что эти данные есть в нашем наборе данных.

Вывод: array([‘no’], dtype=object)
Прогноз — нет, такой же, как и в наборе данных. Теперь спрогнозируем, будет ли диабет у человека 47 лет с индексом массы тела 45. Отмечу, что этих данных в нашем наборе нет.

Вывод: array([‘yes’], dtype=object)

7. Визуализация модели:

Код и набор данных из этой статьи доступны на GitHub.

Приходите изучать математику к нам на курс «Математика и Machine Learning для Data Science» а промокод HABR, добавит 10 % к скидке на баннере.

Рекомендуемые статьи

Источник

Как увидеть лес за деревьями: что такое Decision Tree и зачем это нужно в Big Data

Продолжая насыщать курс Аналитика больших данных для руководителей важными понятиями системного анализа, сегодня мы рассмотрим, что такое дерево решений (Decision Tree). А также расскажем, как этот метод Data Mining и предиктивной аналитики используется в машинном обучении, экономике, менеджменте, бизнес-анализе и аналитике больших данных.

Как растут деревья решений: базовые основы

Начнем с определения: дерево решений – это математическая модель в виде графа, которая отображает точки принятия решений, предшествующие им события и последствия. Этот метод Data Mining широко используется в машинном обучении, позволяя решать задачи классификации и регрессии [1].

Аналитические модели в виде деревьев решений более вербализуемы, интерпретируемы и понятны человеку, чем другие методы Machine Learning, например, нейронные сети. Дополнительное достоинство Decision Tree – это быстрота за счет отсутствия этапа подготовки данных (Data Preparation), поскольку не нужно очищать и нормализовать датасет [2].

В бизнес-анализе, менеджменте и экономике Decision Tree – это отличный инструмент для наглядного отображения всех возможных альтернатив (сценариев), прогнозирования будущих событий, а также оценки их потенциальной выгоды и рисков. Для этого дерево решений представляют в виде графической схемы, чтобы его проще воспринимать и анализировать. Данный граф состоит из следующих элементов [3]:

• вершины, от которых возможно несколько вариантов, называют узлами. Они показывают возможные ситуации (точки принятия решений);
• конечные узлы (листья) представляют результат (значение целевой функции);
• ребра (ветви), соединяющие узлы, описывают вероятности развития событий по этому сценарию.

Обычно многоузловые деревья решений строятся с помощью специального программного обеспечения. Но граф с ограниченным числом вершин можно построить в табличном редакторе или даже вручную. Как это сделать самостоятельно, мы рассмотрим далее на простом примере из управленческой практики.

Строим дерево решений на примере обучения Big Data

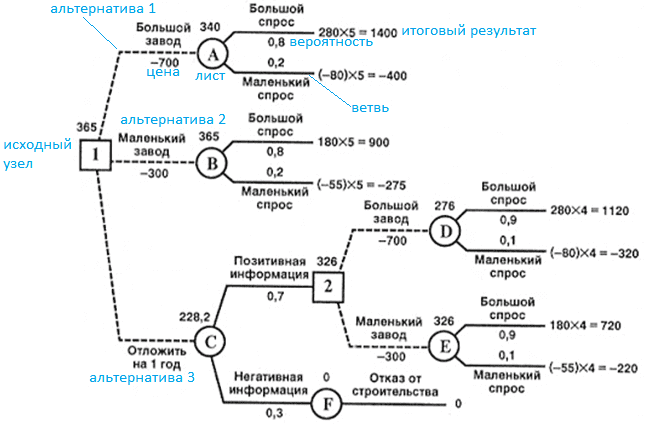
Итак, проанализируем кейс построения дерева решений на примере расчета выгоды от обучения сотрудников новой Big Data технологии с целью быстрого выпуска продукта ценой X. При этом возможны следующие альтернативные сценарии:

• поручить каждому сотруднику самостоятельно освоить нужные подходы, фреймворки и языки программирования в свободное от работы время. Фактические затраты на реализацию такого решения равны нулю, а вероятность успешного освоения технологии для быстрого выпуска продукта оценивается на уровне 30%.
• выделить w рабочих дней на самостоятельное обучение каждого сотрудника на его рабочем месте. Фактические затраты на реализацию такого решения составляют стоимость рабочего дня каждого сотрудника в день (Z), умноженное на количество дней (w) и число сотрудников (k). Успех ожидается в 50% случаев.
• организовать корпоративное обучение всех сотрудников в специализированном учебном центре в течении n дней. Затраты на обучения составят совокупную стоимость курсов (Y), а также цену рабочего дня каждого сотрудника в день (Z)*количество дней (n)*число сотрудников (k). При этом сотрудники освоят технологию с вероятностью 98% за n дней (n

Затраты на реализацию решения

Вероятность успешного освоения технологии для быстрого выпуска продукта ценой X

Самостоятельное обучение каждого сотрудника вне работы

Самостоятельное обучение каждого сотрудника на работе

стоимость рабочего дня каждого сотрудника в день (Z)*количество дней (w)*число сотрудников (k)

Организованные курсы для всех сотрудников в учебном центре

цена обучения (Y) + стоимость рабочего дня каждого сотрудника в день (Z)*количество дней (n)*число сотрудников (k)

Сравнив в абсолютных числах выражения 0,3X, (X*0,5 – Z*w*k) и (X*0,98 – Y – Z*n*k), можно выбрать наиболее выгодный вариант. Таким образом, дерево решений позволяет количественно оценить риски, затраты и выгоды возможных альтернатив и выработать оптимальную управленческую стратегию. Не случайно профессиональный стандарт бизнес-аналитика, руководство BABOK, о котором мы рассказывали здесь, включило дерево решений в набор наиболее часто используемых техник [4]. В следующей статье мы расскажем, как деревья решений и другие методы интеллектуального анализа данных реализуются в новом тренде аналитики больших данных — Augmented Analytics.

Источник