Построить деревья достижимости сетей петри

Анализ сетей Петри

К задачам анализа сетей Петри относятся следующие: безопасность, ограниченность, сохраняемость, активность и ряд других.

Сеть Петри называется безопасной, если в любой маркировке, достижимой из заданной, количество фишек в любой позиции не превышает единицы. Это свойство важно в тех случаях, когда сеть Петри используется для моделирования электронных устройств.

Более общим свойством, чем безопасность, является ограниченность. Говорят, что сеть Петри является k-ограниченной, если в любой достижимой маркировке количество фишек в любой позиции не превосходит k.

В некоторых случаях значение k может быть задано для каждой позиции. Иногда бывает необходимо просто проанализировать возможность или невозможность неограниченного накопления фишек в позиции.

Сеть Петри называется строго сохраняющей, если в любой достижимой маркировке суммарное количество фишек по всем позициям одно и тоже.

При рассмотрении задачи активности анализируется возможность запуска позиции сети Петри. Можно определить различные уровни активности перехода t_j в сети Петри С с маркировкой μ. Уровень активности 0 означает, что переход t_j никогда не сможет быть запущен.

Уровень 1. Переход t_j потенциально запустим, т.е. существует , в которой переход t_j потенциально разрешён.

Уровень 2. Если для всякого целого n существует последовательность запусков, в которой переход t_j присутствует, по крайней мере, n раз.

Уровень 3. Существует такая бесконечная последовательность запусков, в которой переход t_j присутствует неограниченно часто.

Уровень 4. Для любой достижимой маркировки существует такая последовательность запусков σ, что в результате её применения, начиная с маркировки , мы придём к маркировке, в которой переход t_j является разрешённым.

Задача достижимости формулируется следующим образом: для заданной сети Петри С с маркировкой и маркировки необходимо определить, верно ли, что.

Методы анализа сетей Петри. Дерево достижимости

Дерево достижимости представляет собой множество достижимости сети Петри. Рассмотрим следующую сеть Петри.

Error: Reference source not found

При этой маркировке разрешёнными являются переходы t₁ и t₂.

При построении дерева достижимости вначале корню дерева мы выписываем начальную маркировку. Количество разрешённых переходов будет соответствовать количеству дуг, выходящих из данной вершины. Конечные вершины на этих дугах будут соответствовать новым маркировкам.

Построим дерево достижимости.

(2,0,0)

t₁ t₂ t₃

(1,2,1) (0,2,2) (1,0,1)

t₃

При использовании описанной процедуры построения дерева мы можем получить дерево бесконечного размера.

Для превращения дерева достижимости в полезный инструмент необходимо найти средство его ограничения до конечного размера. Первое средство заключается в том, что мы выделяем терминальные вершины, возникающие при пассивных маркировках. Второй класс маркировок – дублирующие вершины, т.е. те маркировки, которые уже возникали ранее.

Для сведения дерева достижимости к конечному можно использовать ещё одно средство.

Рассмотрим последовательность запусков переходов σ, начинающуюся в некоторой маркировке μ. Пусть конечной маркировкой при этом будет μ’, для которой μ’> μ (сравнение идёт покомпонентно), т.е. в некоторых позициях для маркировки μ’ количество фишек будет больше, чем в маркировке μ (в остальных позициях количества фишек будут совпадать).

Условно мы можем записать μ’= μ+( μ’- μ), (μ’- μ)>0. Поскольку лишние фишки не мешают запуску переходов, то мы можем последовательность переходов σ запустить, начиная с маркировки μ’ и получить маркировку μ”= μ’+( μ’- μ)= μ+2(μ’- μ).

Таким образом, мы можем бесконечно увеличивать количество фишек в некоторых позициях.

Представим значение “” в маркировке символом ω. Будем считать, что для любого постоянного значения а ω+а=ω и ω-а=ω.

Алгоритм формирования дерева достижимости: каждая вершина i дерева достижимости связана с расширенной маркировкой μ[i]. В этой маркировке число фишек может быть либо неотрицательным целым, либо бесконечным, обозначаемым ω. Каждая вершина дерева может быть одного из четырёх типов:

1. граничная

1. терминальная

1. дублирующая
2. внутренняя

Граничными являются вершины, которые ещё не обработаны алгоритмом. Алгоритм превратит их в терминальные или дублирующие, или внутренние (породив, возможно, при этом некоторый набор граничных вершин). Пусть х – граничная вершина, которую необходимо обработать.

1. Если в дереве достижимости имеется другая вершина y, не являющаяся граничной, такая, что μ[у]= μ[х], то вершина х становится дублирующей.

1. Если для маркировки μ[х] ни один из переходов не разрешён, то вершина х становится терминальной.

1. Для всякого перехода , разрешённого в маркировке μ[х], необходимо создать новую вершину z дерева достижимости. Маркировка μ[z], связанная с этой вершиной, для каждой позиции определяется следующим образом:

а) Если μ[х]_i=ω, то μ[z]_i=ω. б) Если на пути от корневой вершины к вершине х существует вершина у такая, что маркировка μ[у]<δ(μ[х], t_j) и, кроме того, в μ[у]_i<δ(μ[х], t_j)_i, то μ[z]_i=ω. в) В противном случае μ[z]_i= δ(μ[х], t_j)_i. Дуга помечается запущенным переходом t_j, которая направляется от вершины х к вершине z дерева достижимости. Вершина z помечается как граничная. После просмотра всех переходов, которые можно запустить при маркировке μ[х], вершина х помечается как внутренняя. Прекращение работы алгоритма осуществляется тогда, когда в дереве достижимости не останется граничных вершин. Основным свойством алгоритма построения дерева достижимости является то, что он заканчивает свою работу. Для доказательства этого необходимо показать, что алгоритм не может создавать новых граничных вершин бесконечно. Доказательство основано на трёх леммах. Лемма 1. В любом бесконечном направленном дереве, в котором всякая вершина имеет только конечное число непосредственно следующих вершин, существует бесконечный путь, исходящий из корня. Лемма 2. Всякая бесконечная последовательность неотрицательных целых чисел содержит бесконечную неубывающую подпоследовательность. Лемма 3. 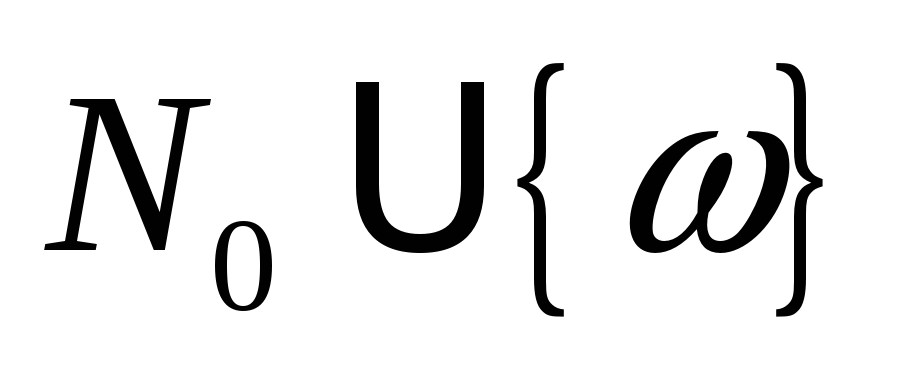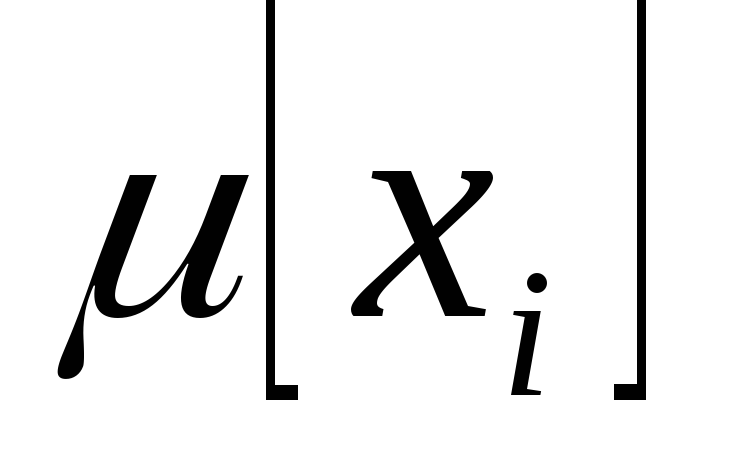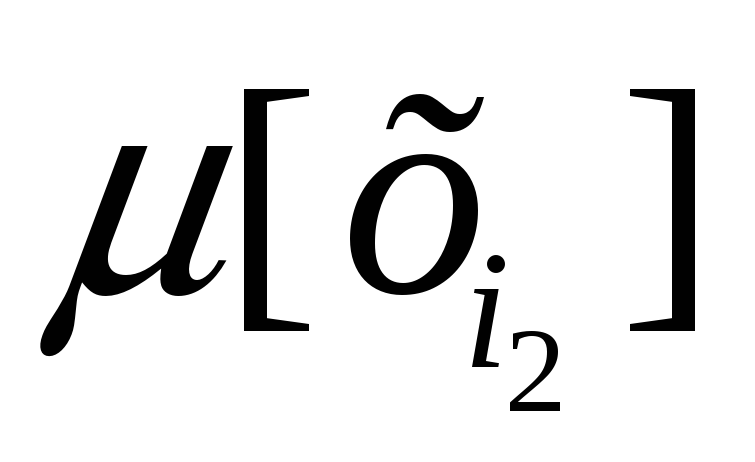Всякая бесконечная последовательность n-мерных векторов, содержащих элементы как неотрицательные целые числа , содержит бесконечную неубывающую подпоследовательность. Теорема: дерево достижимости сети Петри конечно. Доказательство: Предположим противное, т.е. существует бесконечное дерево достижимости. Тогда, согласно Лемме 1, в нём имеется бесконечный путь х₀,х₁,х₂,…, исходящий из корня х_0. Тогда мы имеем μ[х₀], μ[х₁], μ[х₂],…, бесконечную последовательность n-мерных векторов со значениями, которые определены в Лемме 3. Согласно ей должна существовать бесконечная неубывающая подпоследовательность . Но, согласно алгоритму, мы не можем иметь ситуации, что , поскольку одна из этих вершин была бы дублирующей и не имела бы продолжений. Таким образом, мы имеем последовательность строго возрастающих маркировок . Но по построению дерева достижимости, если , то нам следует заменить хотя бы одну компоненту маркировки на символ ω. Таким образом, для имеющейся последовательности мы имеем, что содержит, по крайней мере, один символ ω. — по крайней мере, два символа ω и т.д. Т.е. не далее, чем маркировка содержит все n символов ω, а это означает, что следующая маркировка подпоследовательности уже не может быть строго больше, чем . Полученное противоречие доказывает конечность дерева достижимости. Использование дерева достижимости позволяет решать поставленные ранее задачи анализа сетей Петри. Для этого необходимо будет просмотреть узлы дерева достижимости. 6

Источник

Сети Петри. Анализ дискретных систем с помощью сетей Петри , страница 7

Существуют два основных метода анализа сети, базирующихся на гра-фическом или математическом их представлении. К ним относятся метод, использующий дерево достижимости, и метод, использующий матричные уравнения. Рассмотрим эти методы.

2.2.1. Дерево достижимости

Деревом достижимости называется ориентированный древесный граф, вершинами которого являются разметки сети — m, а дуги взвешены переходами и связывают непосредственно достижимые маркировки. На рис. 2.5 приведен граф сети Петри. Построим для данного графа дерево достижимости.

Рис. 2.5. Пример графа сети Петри для построения дерева достижимости

Вектор m = (1, 0, 0, 0) задает исходную маркировку сети Петри. Она является корнем дерева достижимости. Построение дерева начинается с корня, то есть с исходной маркировки. При срабатывании перехода t₁ будет получена маркировка m’ = (0, 1, 0, 0). Далее может сработать один из двух переходов: переход t₂ или переход t₃. При срабатывании перехода t₂ будет получен вектор m’’ = (0, 0, 1, 0). Вектор m’’’ = (0, 0, 0, 1) будет получен при срабатывании перехода t₃. На этом функционирование сети Петри завершится.

Построим дерево достижимости (рис. 2.6). На основе дерева достижимости можно определить и решать различные задачи анализа сети Петри. Рассмотрим примеры решения таких задач для дерева достижимости, приведенного на рис. 2.6.

1. При решении задачи достижимости маркировки m = (0, 0, 0, 0) можно сделать вывод, что такая маркировка недостижима, так как соответствующей вершины на дереве нет.

2. Решение задачи безопасности позволяет сделать вывод, что сеть безопасна, так как в каждой позиции не больше одной метки во всех возможных маркировках.

3. Результатом решения задачи сохраняемости является вывод, что сеть является строго сохраняющей. Данный вывод основан на том, что во всех вершинах дерева общее число фишек равно одной.

Рис. 2.6. Пример дерева достижимости

Все задачи решаются простым перебором сети дерева достижимости в силу того, что дерево конечно.

Если множество достижимости сети Петри бесконечно, то для использования дерева нужно его представить конечным графом. В этом случае вводятся дополнительные правила для представления бесконечного процесса конечным. На рис. 2.7 приведен фрагмент бесконечного дерева достижимости для сети Петри, приведенной на этом же рисунке. Данная сеть и дерево достижимости описывают циклический процесс. Так как здесь нет правил выхода из цикла, то процесс является бесконечным.

Для исключения бесконечных циклов, а следовательно представления бесконечного дерева конечным, вводится понятие дублирующей вершины. Если на пути от корневой вершины к текущей находится маркировка, совпадающая с текущей, то текущая вершина называется дублирующей. Для такой вершины исходящих дуг на дереве достижимости нет, так как все возможные маркировки на дереве уже существуют и нет необходимости их повторять.

Рис. 2.7. Пример бесконечного дерева достижимости: а) сеть Петри; б) фрагмент бесконечного дерева достижимости для приведенной сети Петри; в) конечное дерево достижимости

В рассматриваемом примере маркировка (1, 0, 0) определяет вершину, являющуюся дублирующей. Поэтому этой вершиной завершается построение дерева достижимости.

Если сеть не является ограниченной и сохраняющей, возможно бесконечное накопление фишек в ее позициях. Для построения конечных деревьев достижимости в этом случае вводится символ бесконечности — w. Маркировка, содержащая такой символ, называется расширенной маркировкой. Для данного символа справедливы операции сложения: w = w + n и вычитания: w = w – n, где n — конечное целое число.

Источник