Правило леонардо о дереве

Лесная математика

Человечество тысячи лет жило рядом с деревьями, но нам понадобился Леонардо да Винчи, чтобы заметить скрытые от беглого взгляда математические закономерности в лесу.

В записных книжках Леонардо да Винчи говорится: «Толщина всех веток дерева на любой его высоте, сложенная вместе, дает толщину ствола». Художник считал, что это применимо ко всем ветвящимся природным системам вроде рек, ручьев и кровеносных сосудов, но в наши дни «правилом Леонардо» называют только соотношение толщины ветвей у деревьев. В современной формулировке оно звучит так:

«Сумма площади поперечного сечения всех ветвей дерева выше точки ветвления на любой высоте равна площади поперечного сечения ствола или ветви непосредственно ниже точки ветвления».

Конечно, такая пропорция не всегда соблюдается с идеальной точностью, но любые отклонения только подтверждают незыблемость правила.

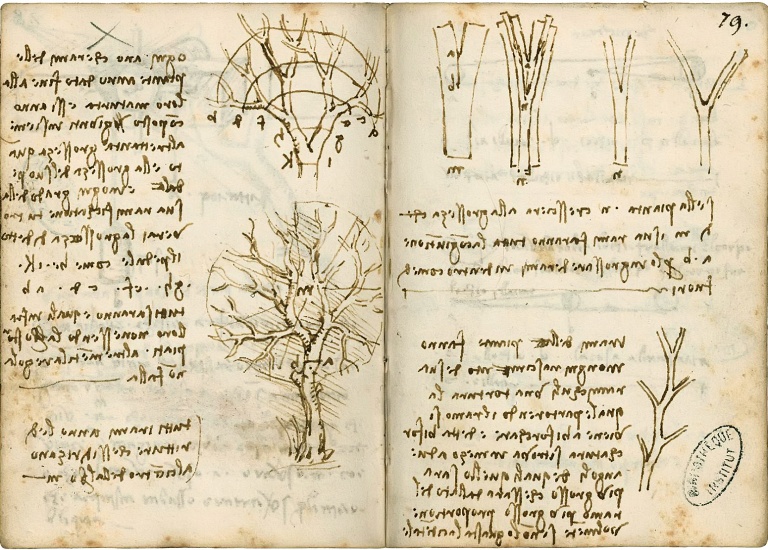
Наброски и записи из тетрадей Леонардо. museoteca.com

Ученые сотни лет принимали «правило Леонардо» за аксиому и лишь недавно попытались объяснить, почему деревья растут именно так. Кристоф Элой (Christophe Eloy), физик из Калифорнийского университета, в 2011 году впервые предположил, почему правило Леонардо хорошо работает в природе. Он создал математическую модель, в которой для простоты расчетов дерево описывалось как ветвящаяся фрактальная структура, неподвижная в нижней точке, что соответствует месту ухода ствола под землю. («ММ» писал о фракталах в номере за февраль 2020 года. – Ред.) Добавив к модели давление ветра, Элой вычислил предельную величину, после которой ветви начнут ломаться. Он использовал две модели ветрового давления: в одном случае сила прикладывалась к концу ветви, как обычно бывает, когда ветер действует в основном на листья, а во втором воздействие оказывалось на сами ветки. Рассчитав оптимальную толщину разветвляющихся веток, при которой сопротивление ветру в том и другом случае было бы наилучшим, Элой обнаружил, что она в точности совпадает с правилом Леонардо.

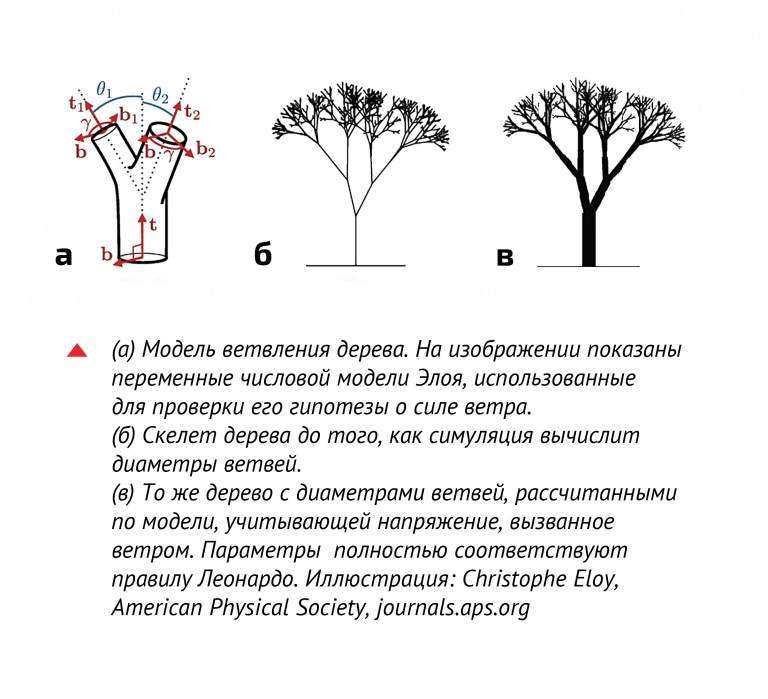
Кристоф считает, что мы имеем дело со способностью дерева приспосабливаться к внешнему фактору: ветер, действуя на растение, заставляет учитывать дополнительную нагрузку. Хорошо защищенные от ветра деревья вырастают выше контрольных образцов, но при этом они ломаются легче, чем деревья того же вида, растущие на открытом месте. Это можно заметить и в природе, сравнивая деревья в густых лесах и на открытых участках.

В 2013 году биологи Рюко Минамино и Масаки Татено (Ryoko Minamino, Masaki Tateno) из ботанического сада при Токийском университете провели исследование, на которое способны только терпеливые японцы. Они тщательно измерили сечения ветвей хвойных и лиственных деревьев, выбрав в качестве образцов бук и пихту, а потом определили их упругость, сопротивление на излом и величину изгиба, вызванного собственной тяжестью. Для этого некоторые ветки пришлось спилить, чтобы сравнить их деформацию на живом дереве и лабораторном столе.

Биологи измерили углы, под которыми меньшие ветви отходили от больших, подсчитали среднее число «дочерних» ветвей и свели все значения воедино. Они пришли к выводу, что в ряде случаев деревья следуют правилу Леонардо вместо того, чтобы развиваться максимально выгодным образом для обеспечения прочности своих ветвей. По мнению ученых, дерево может компенсировать подобный недостаток невидимым снаружи способом, изменяя внутреннюю структуру древесины. Количество «дочерних» ветвей ничего не меняло: сколько бы их ни отходило от «материнской» ветви, правило Леонардо все равно соблюдалось. Красота и элегантность математической модели оказались сильнее внешних воздействий. Быть может, ученые, считающие Вселенную великой компьютерной симуляцией, как в фильме «Матрица», оказались ближе к истине, чем мы до сих пор думали.

Источник

Правило Леонардо да Винчи

Люди видят деревья в каждый день, но никто даже не задумывался, почему деревья растут таким образом. А Леонардо да Винчи, пытаясь нарисовать дерево, когда-то заметил: дерево почти всегда растет таким образом, что толщина всех веток дерева на любой его высоте, сложенная вместе, дает толщину ствола (рис. 1). Почему деревья так растут? Еще никто не сумел объяснить. Ученые проводили много исследований, чтобы это доказать. В результате исследования они убедились, что правило хорошо выполняется. А почему это так происходит неизвестно. Рисунок 1 – Работа Леонардо да Винчи Опишем правило на математическом языке. Оно говорит, что если ветка с диаметром (D) делится на произвольное число (n) вторичных ответвлений диаметром (d1, d2 и т.д. соответственно), сумма квадратов диаметров вторичных ответвлений будет равна квадрату диаметра первичной ветви (рис.2). Или в виде формулы: , где– это количество ответвлений. Это уравнение достаточно близкое почти для всех видов деревьев.[1] Рисунок 2 – Правило Леонардо да Винчи

Измерительные работы

В своей работе мы решили проверить это правило на деревьях, которые растут у нас возле школы. Мы осмотрели все деревья, которые находятся на пришкольном участке, из них выбрала 4 дерева (рябину и яблоню, березу и клен), которые подходят для измерений. Нам нужны были правильные деревья, чтобы разветвление веток было на удобной высоте. Нам необходимо было найти способ измерения диаметра дерева не прибегая к его распилу. Для того чтобы измерить диаметр ствола дерева, нам пригодилась только измерительная лента и несколько формул. Чтобы не пилить деревья, люди придумали очень удобный способ измерения. Мы измерили обхват ствола на высоте 30-40 сантиметров от земли. Затем поднялись на один — два уровня выше, где дерево разветвляется, и так же измерили на определенной высоте каждую ветку. Обхват является длиной окружности. С помощью формулы для вычисления длины окружности я нашла радиус. или , где (рис.3) [2] Рисунок 3 – Окружность Результаты вычислений занесли в таблицу (см. таб.1). L11 – это обхват дерева на первом уровне, L21, L22, … — обхват каждой ветки на втором уровне, L31, L32, … — на третьем. Таблица 1 – Результаты измерений и вычислений

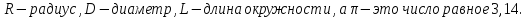
Вид дерева	Обхват дерева(l, )	Диаметр среза(D, )	Сумма диаметров в каждом ряду
Яблоня
1 ряд	L11 = 123	D11=39	39
2 ряд	L21 = 20, L22 = 66, L23 = 47	D21 = 6, D22 = 21, D23 = 15	42
3 ряд	L31 = 30, L32 = 23, L33 = 44, L34 = 45, L35 = 16, L36 = 30	D31 = 10, D32 = 7, D33 = 14, D34 = 14, D35 = 5, D36 = 10	50
Рябина
1 ряд	L11 = 79	D11 = 25	25
2 ряд	L21 = 40, L22 = 45	D21 = 13, D22 = 14	27
3 ряд	L31 = 28, L32 = 27, L33 = 32, L34 = 30	D31 = 9, R32 = 9, D33 = 10, D34 = 10	38
Береза
1 ряд	L11 = 149 + 38	D11 = 47+12	59
2 ряд	L21 = 100, L22 = 99	D21 = 32, D22 = 32	64
3 ряд	L31 = 59, L32 = 80, L33 = 38, L34 = 72	D31 = 19, D32 = 25, D33 = 12, D34 = 23	79
Клен
1 ряд	L11 = 189	D11 = 60	60
2 ряд	L21 = 72, L22 = 60+15, L23 = 69+10, L24 = 100	D21 = 23, D22 = 24, D23 = 25, D24 = 32	104

Для продолжения скачивания необходимо пройти капчу:

Источник

Правило Леонардо да Винчи

Когда деревья сбрасывают листву осенью, они раскрывают загадочный, почти универсальный характер роста, впервые наблюдаемый Леонардо да Винчи 500 лет назад: простые, но поразительные взаимоотношения, которые почти всегда находятся в прямой зависимости между размером ствола и размеров его ветвей. Одна из новых гипотез снова разожгла дебаты, почему деревья растут таким образом, утверждая, что они может быть защищают себя от повреждения ветром.

«Правило Леонардо — удивительная вещь,» заявила Kate McCulloh из Университета штата Орегон, ученый, специализирующийся на физиологии растений. «До недавнего времени люди действительно это не проверяли и не обращали внимания.» Да Винчи писал в своей записной книжке, что «все ветви дерева на каждом этапе его высоты, вместе взятые равны по толщине самому стволу.» Другими словами, если ветви дерева сложить вверх и сжать вместе, дерево будет выглядеть как один большой ствол с одинаковой толщиной сверху донизу.

Чтобы выяснить, почему это правило может существовать, физик Christophe Eloy из университета Прованса во Франции, сгенерировал на компьютере деревья с замысловатыми ветвящимися паттернами веток. «Я разработал легкую древовидную структуру, чтобы противостоять ветру, сохраняя при этом прочность ствола», сказал Элой. Деревья являются фракталом в природе, это означает, что узоры, созданные крупными структурами, таких как основные стволы, повторяются в небольших структурах, таких как мелкие ветви.

Элой начал со скелета фрактального дерева, в котором уменьшенные копии основных ветвей неоднократно суммируются для создания виртуального дерева. Каждая новая ветвь берет начало из «материнской» ветви, имитируя фрактальный характер реальных деревьев. На данном этапе, модель дерева служила лишь в качестве основы для последующего определения наиболее эффективной толщины ветви.

После того, как скелет был завершен, Элой поместил его на испытания в виртуальную аэродинамическую трубу. После применения различных ветровых сил, необходимых для разрушения ветви, Элой определил диаметры для каждой ветви, что ограничивало возможность привязки. Учет каждой части от наименьшей ветки к стволу показалось симуляцией правила Леонардо. В дальнейшем, добавив к этой модели такую переменную, как давление ветра, Эллой ввел определенный постоянный показатель его предельной величины, после которой ветви начинают ломаться. После произведенных расчетов, которые показали оптимальную толщину разветвляющихся веток, при которой сопротивление силе ветра было наилучшим, он пришел к тем же выводам.

Слева – созданной Кристофом Элоем модели, использованной для доказательства его гипотезы. Справа – фрактальный «скелет» модели дерева до того, как алгоритм начал менять диаметры его ствола и ветвей, подбирая оптимальные величины.

Элой обнаружил, что пропорции в его модельных деревьях остались прежними, независимо от скорости ветра или высоты ветвей, как и было предсказано правилом. Его работа была принята к публикации в журнале Physical Review Letters.

Тем не менее, некоторые ученые считают, что должно быть нечто больше, в правиле Леонардо чем предполагает Элой в своих исследованиях.

Пояснения к правилу как правило, делятся на две категории — гидрологические и структурные. Гидрологические теории предполагают, что деревья имеют свою характерную форму, потому что это способствует эффективности транспортировать сок, в то время как структурные объяснения сосредотачиваются на способности деревьев выдерживать нагрузку. С его новым исследованиям Элой укрепил структурную теорию. «Я не сомневаюсь, что структура дерева является результатом сочетания гидравлики и структурных ограничений» — сказал Gil Bohrer, инженер-эколог в Университете штата Огайо в Колумбусе, «Тем не менее, я не думаю, что гидрологический аргумент должен быть отклонен так легко.»

Независимо от причины, почему правило Леонардо имеет место, данные, собранные в этой области показали, что деревья многих видов подчиняются правилу. Хотя доказательства до сих пор подтверждают 500-летнее правило, это может быть довольно нудно, чтобы твердо подтвердить наблюдение да Винчи. «[Экспериментальные] данные очень рассеяны,» сказал Элой. «Если вы смотрите на большие деревьев, у него есть тысячи ветвей, и это занимает много человеческих ресурсов, чтобы измерить все ветви.» Хотя есть небольшие экспериментальные данные применения наблюдения да Винчи, его правило широко используется в компьютерной графике и математическом искусстве.

Robert Fathauer — физик и инженер по образованию превратился в математического художника — им изучался мир фрактальных деревьев в течение многих лет. Он использует процесс, аналогичный исследований Eloy для создания своих работ. Fathauer использует фотографию одного разделения или бифуркации между стволом и ветви в качестве строительного блока для всей его части. Затем он неоднократно добавляет уменьшенную версию оригинального строительного блока с планом дерева. В то время как он не включает правило Леонардо в работу непосредственно, правило всплывает в его работах через фотографии реальных деревьев.

Ниже представлены одни их многих его работ:

«Я не сознательно использовал [правило Леонардо] для моего искусства», сказал Fathauer. «Но когда я начал сравнивать площадь поверхности всей разветвлений, я нашел экспериментальное подтверждение, что правило Леонардо работает довольно хорошо.»

Ученые надеются, что дальнейшие исследования этого правила раскроют больше о ветре, структуре леса и эволюции деревьев.

Источник