Префиксная форма обхода дерева

15.5.6. Алгоритмы обхода дерева

Существуют три алгоритма обхода деревьев, которые естественно следуют из самой структуры дерева.

1. Обход слева направо: Left-Root-Right (сначала посещаем левое поддерево, затем – корень и, наконец, правое поддерево).

2. Обход сверху вниз: Root-Left-Right (посещаем корень до поддеревьев).

3. Обход снизу вверх: Left-Right-Root (посещаем корень после поддеревьев).

Интересно проследить результаты этих трех обходов на примере записи формулы в виде дерева, так как они и позволяют получить различные формы записи арифметических выражений.

Пусть для операндов А и В выполня­ется операция сложения. Привычная форма записи в виде А+В называется ин­фиксной. Форма записи, в которой знак операции следует перед операндами +АВ, называется префиксной, если же операция записывается после операндов АВ+ – постфиксной.

Рассмотрим небольшой пример, пусть задано выражение А+В*С. Так как умножение имеет более высокий приоритет, то данное выражение можно переписать в виде А+(В*С). Для записи выражения в постфиксной форме сначала преобразуем ту часть выражения, которая вычисляется первой, в результате получим: А+(ВС*).

Теперь запишем в постфиксной форме операцию сложения между операндами А и (ВС*): АВС*+.

Таким образом, выражение А+В*Св постфиксном видеАВС*+, префиксная форма записи будет иметь вид +*АВС.

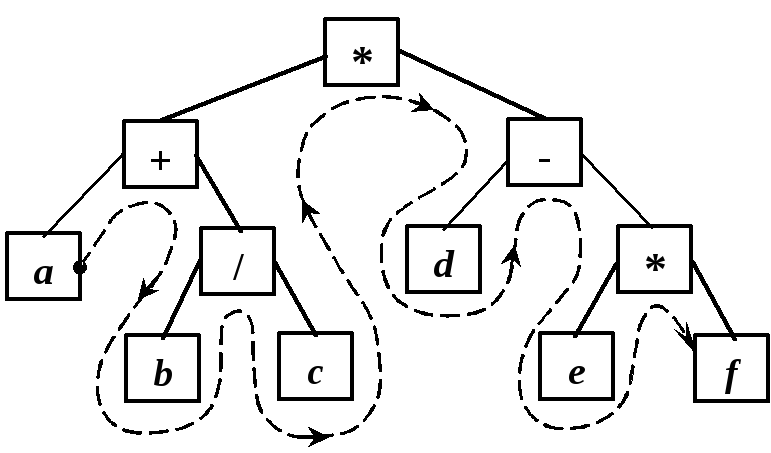
Рассмотрим различные обходы дерева на примере формулы: ((a+b/c)*(d–e*f )). Дерево формируется по принципу:

– в корне размещаем операцию, которая выполнится последней;

– далее узлы-операции, операнды – листья дерева.

Обход 1 (Left-Root-Right) дает обычную инфиксную запись выражения (без скобок):

a + b / c * d – e * f .

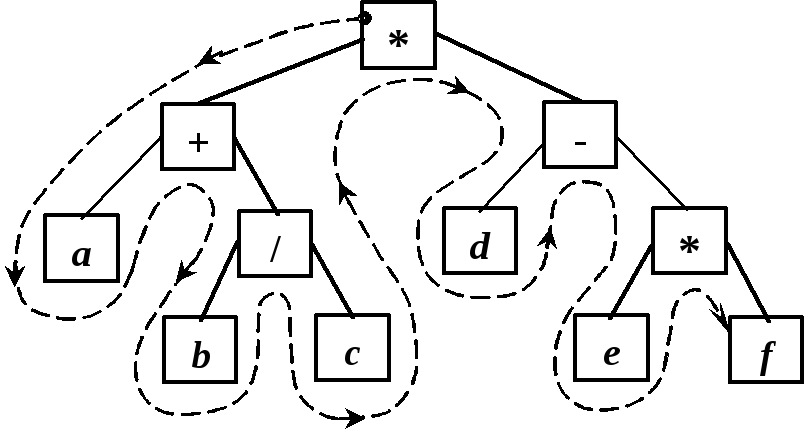
Обход 2 (Root-Left-Right) – префиксную запись выражения (без скобок):

* + a / b c – d * e f .

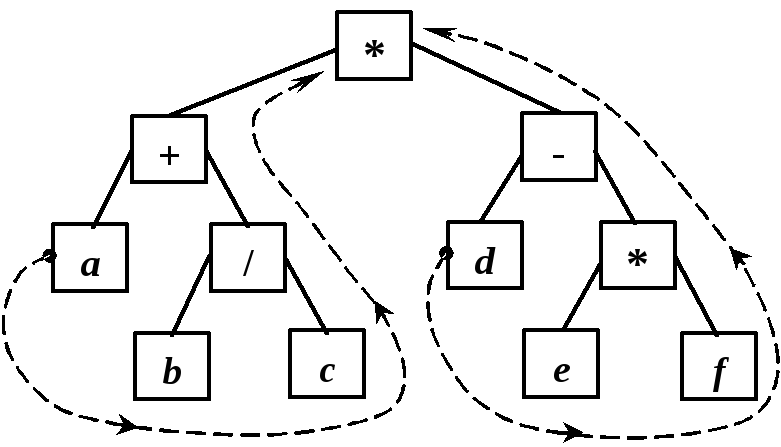
Обход 3 (Left—Right—Root) – постфиксную запись выражения:

15.5.7. Функция просмотра

Приведем простой пример функции вывода элементов (ключей) дерева, использующий правила обхода 2.

void View ( Tree *t, int level )

View(t->Right,level+1); // Вывод правого поддерева

View(t->Left,level+1); // Вывод левого поддерева

Обращение к функции Viewбудет иметь видView(Root, 0);

Функция View рекурсивная, вторым ее параметром является переменная, определяющая, на каком уровне (level) находится узел. Корень находится на уровне «0». Значения узлов выводятся по горизонтали так, что корень находится слева. Перед значением узла для имитации структуры дерева выводится количество пробелов, пропорциональное уровню узла. Если закомментировать цикл печати пробелов, значения ключей будут выведены просто в столбик.

Для последовательно введенных ключей 10 (корень), 25, 20, 6, 21, 8, 1, 30, будет построено дерево, вывод которого на экран с помощью функции Viewбудет иметь следующий вид:

15.5.8. Освобождение памяти

Функция освобождения памяти, занятой элементами дерева, может быть реализована аналогично рекурсивной функции View

Источник

Методы программирования

Задание состоит из трех частей, первая и третья обязательны для выполнения, вторая выполняется по желанию студента. Срок сдачи задания — 17 октября.

Теория

Двоичное дерево задается следующей структурой:

typedef struct _t int data; /* данные в узле */
struct _t *left, *right; /* указатели на левого и правого сыновей */
> t;

t *root; /* корень дерева */

Таким образом, каждый элемент дерева содержит некоторые данные и два указателя на потомков (на левого сына и на правого). Сам узел будем называть отцом этих двух потомков. Определение дерева требует, чтобы у каждого узла, кроме корня, был ровно один отец. Указатель на корень дерева хранится в переменной root , она равна нулю, если дерево пусто.

Левым и правым поддеревьями узла t ( t != 0 ) будем называть деревья (возможно, пустые), корнями которых являются соответственно t->left и t->right .

Основные операции на деревьях: поиск элемента, добавление элемента, удаление элемента. Для поиска элемента в произвольном бинарном дереве необходимо обойти все элементы этого дерева. Существует два основных способа обхода дерева: в глубину и в ширину.

Обход дерева в глубину

Обход в глубину производится рекурсивно либо с использованием стека. В обоих случаях можно обходить узлы дерева в различной последовательности. Обход начинается от корня. Выделяют три наиболее важных порядка обхода в глубину:

• префиксный (прямой) обход — сначала обрабатывается текущий узел, затем левое и правое поддеревья;
• инфиксный (симметричный) обход — сначала обрабатывается левое поддерево текущего узла, затем корень, затем правое поддерево;
• постфиксный (обратный) обход — сначала обрабатываются левое и правое поддеревья текущего узла, затем сам узел.

В качестве примера рассмотрим следующее дерево:

• префиксный обход: A, B, D, H, E, C, F, I, J, G
• инфиксный обход: D, H, B, E, A, I, F, J, C, G
• постфиксный обход: H, D, E, B, I, J, F, G, C, A

Запишем в качестве примера рекурсивную процедуру, выводящую на экран узлы дерева в порядке префиксного обхода.

void prefix(t *curr)
if (!curr)
return;
printf(«%d «, curr->data);
prefix(curr->left);
prefix(curr->right);
>

Обход дерева в ширину

Обход в ширину производится с помощью очереди. Первоначально в очередь помещается корень, затем, пока очередь не пуста, выполняются следующие действия:

• Из очереди выталкивается очередной узел;
• Этот узел обрабатывается;
• В очередь добавляются оба сына этого узла.

Узлы дерева на рисунке перечисляются в порядке обхода в ширину следующим образом: A, B, C, D, E, F, G, H, I, J. Заметим, что перечисление узлов происходит в порядке удаления от корня, что делает поиск в ширину удобным, например, для поиска узла дерева со значением k , наиболее близкого к корню, и т.д.

Приведем пример процедуры, которая выводит на экран узлы дерева в порядке обхода в ширину. Считаем, что определены три функции:

void add(t *elem); /* добавляет в конец очереди элемент elem */
t *del(); /* удаляет из очереди первый элемент и возвращает указатель на него */
int empty(); /* возвращает 1, если очередь пуста, и 0 в противном случае */

Тогда процедура обхода будет иметь следующий вид:

void width(t *root)
if (!root)
return;
add(root);
while (!empty()) t *curr = del();
printf(«%d «, curr->data);
if (curr->left)
add(curr->left);
if (curr->right)
add(curr->right);
>
>

Двоичные деревья поиска

Для поиска узла в таком дереве можно использовать как рекурсивную функцию, так и простой цикл. Ниже приведен пример функции, которая ищет узел со значением k в двоичном дереве поиска с корнем root . Этот код весьма напоминает обычный бинарный поиск:

t *search(t *root, int k)
t *curr = root;
while (curr) if (k == curr->data)
return (curr);
if (k < curr->data)
curr = curr->left;
else
curr = curr->right;
>
return (0);
>

Добавление узла в двоичное дерево поиска напоминает добавление элемента в середину связанного списка: выполняется проход по дереву с запоминанием указателя на узел, предшествующий текущему, и добавление узла к предыдущему, как только текущий указатель станет равным нулю. Необходимо отдельно обработать случай пустого дерева.

Удаление узла из двоичного дерева поиска является менее тривиальной операцией: необходимо поддерживать выполнение условия расположения элементов («слева меньше, справа больше»). Одним из возможных способов является следующий:

• если у удаляемого узла нет сыновей, его удаление не представляет проблемы (освобождаем память и зануляем указатель на нее у его отца);
• если у удаляемого узла есть ровно один сын, удаляем узел, а указатель на него у отца заменяем указателем на этого сына;
• если у удаляемого узла есть оба сына, ищем в правом поддереве узел с минимальным значением (у него по определению будет отсутствовать левый сын) и ставим этот узел на место удаляемого, аккуратно поменяв все необходимые указатели.

Сбалансированные деревья

При работе с двоичными деревьями поиска возможен случай, когда дерево по сути примет вид линейного связанного списка (например, если элементы подавались на вход в порядке возрастания). В таком случае поиск элемента в дереве будет занимать линейное время. Одним из способов предотвращения подобной ситуации является балансировка дерева по мере добавления элементов.

Сбалансированным деревом (AVL-деревом) называется двоичное дерево поиска, удовлетворяющее следующему условию: для любого узла глубина левого поддерева отличается от глубины правого поддерева не более чем на 1. В сбалансированном дереве поиск элемента выполняется за время O(log₂N), где N — количество узлов (Адельсон-Вельский, Ландис, 1962). Алгоритм построения сбалансированных деревьев можно найти в сети и в литературе (Вирт, Кнут, . ), поэтому подробное описание его здесь не приводится.

Формулировка задания

а. Реализация простых двоичных деревьев поиска

Во входном файле input.txt в первой строке находится количество записей N , в следующих N строках находятся записи вида имя значение , причем имена могут повторяться. В файл output.txt выдать итоговые значения всех переменных в алфавитном порядке. Хранение записей организовать в виде двоичного дерева поиска.

Примеры

b. ** Реализация сбалансированных деревьев

Задание аналогично предыдущему, но требуется поддерживать дерево сбалансированным. Задание не является обязательным.

c. Реализация префиксного, инфиксного и постфиксного обходов двоичного дерева

Необходимо реализовать функции обхода дерева в порядке префиксного, инфиксного и постфиксного обходов. Дерево задается произвольным образом.

Источник

15.5.6. Алгоритмы обхода дерева

Существуют три алгоритма обхода деревьев, которые естественно следуют из самой структуры дерева.

1. Обход слева направо: Left-Root-Right (сначала посещаем левое поддерево, затем – корень и, наконец, правое поддерево).

2. Обход сверху вниз: Root-Left-Right (посещаем корень до поддеревьев).

3. Обход снизу вверх: Left-Right-Root (посещаем корень после поддеревьев).

Интересно проследить результаты этих трех обходов на примере записи формулы в виде дерева, так как они и позволяют получить различные формы записи арифметических выражений.

Пусть для операндов А и В выполня­ется операция сложения. Привычная форма записи в виде А+В называется ин­фиксной. Форма записи, в которой знак операции следует перед операндами +АВ, называется префиксной, если же операция записывается после операндов АВ+ – постфиксной.

Рассмотрим небольшой пример, пусть задано выражение А+В*С. Так как умножение имеет более высокий приоритет, то данное выражение можно переписать в виде А+(В*С). Для записи выражения в постфиксной форме сначала преобразуем ту часть выражения, которая вычисляется первой, в результате получим: А+(ВС*).

Теперь запишем в постфиксной форме операцию сложения между операндами А и (ВС*): АВС*+.

Таким образом, выражение А+В*Св постфиксном видеАВС*+, префиксная форма записи будет иметь вид +*АВС.

Рассмотрим различные обходы дерева на примере формулы: ((a+b/c)*(d–e*f )). Дерево формируется по принципу:

– в корне размещаем операцию, которая выполнится последней;

– далее узлы-операции, операнды – листья дерева.

Обход 1 (Left-Root-Right) дает обычную инфиксную запись выражения (без скобок):

a + b / c * d – e * f .

Обход 2 (Root-Left-Right) – префиксную запись выражения (без скобок):

* + a / b c – d * e f .

Обход 3 (Left—Right—Root) – постфиксную запись выражения:

15.5.7. Функция просмотра

Приведем простой пример функции вывода элементов (ключей) дерева, использующий правила обхода 2.

void View ( Tree *t, int level )

View(t->Right,level+1); // Вывод правого поддерева

View(t->Left,level+1); // Вывод левого поддерева

Обращение к функции Viewбудет иметь видView(Root, 0);

Функция View рекурсивная, вторым ее параметром является переменная, определяющая, на каком уровне (level) находится узел. Корень находится на уровне «0». Значения узлов выводятся по горизонтали так, что корень находится слева. Перед значением узла для имитации структуры дерева выводится количество пробелов, пропорциональное уровню узла. Если закомментировать цикл печати пробелов, значения ключей будут выведены просто в столбик.

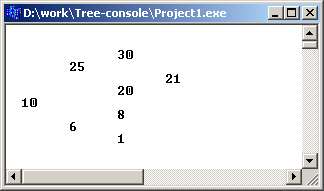
Для последовательно введенных ключей 10 (корень), 25, 20, 6, 21, 8, 1, 30, будет построено дерево, вывод которого на экран с помощью функции Viewбудет иметь следующий вид:

15.5.8. Освобождение памяти

Функция освобождения памяти, занятой элементами дерева, может быть реализована аналогично рекурсивной функции View

Источник