Trie, или нагруженное дерево
Здравствуй, Хабрахабр. Сегодня я хочу рассказать о такой замечательной структуре данных как словарь на нагруженном дереве, известной также как префиксное дерево, или trie.
Что это ?
Нагруженное дерево — структура данных реализующая интерфейс ассоциативного массива, то есть позволяющая хранить пары «ключ-значение». Сразу следует оговорится, что в большинстве случаев ключами выступают строки, однако в качестве ключей можно использовать любые типы данных, представимые как последовательность байт (то есть вообще любые).
Как это работает ?
Нагруженное дерево отличается от обычных n-арных деревьев тем, что в его узлах не хранятся ключи. Вместо них в узлах хранятся односимвольные метки, а ключем, который соответствует некоему узлу является путь от корня дерева до этого узла, а точнее строка составленная из меток узлов, повстречавшихся на этом пути. В таком случае корень дерева, очевидно, соответствует пустому ключу.
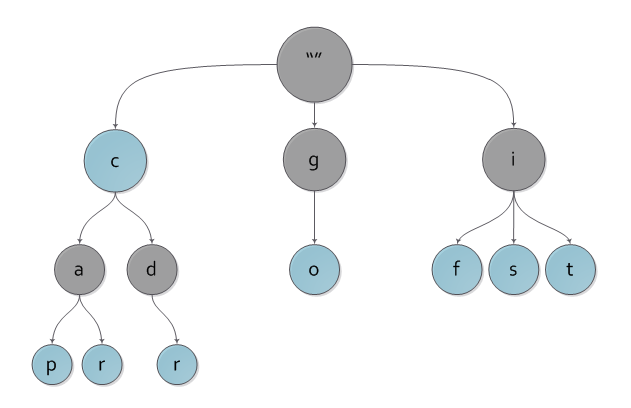
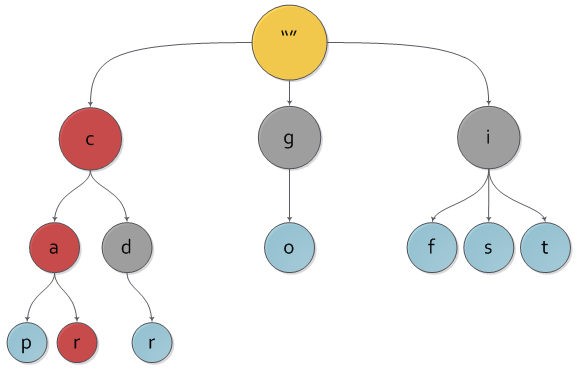
На рисунке вы можете наблюдать пример нагруженного дерева с ключами c, cap, car, cdr, go, if, is, it.
Сразу видно, что наше дерево содержит «лишние» ключи, ведь любому узлу дерева соответствует единственный путь до него от корня, а значит и некоторый ключ. Чтобы избежать проблемы с «лишними» ключами, каждому узлу дерева добавляется булева характеристика, указывающая, является ли узел реально существующим либо промежуточным по дороге в какой-либо другой.
Основные операции
Так как нагруженное дерево реализует интерфейс ассоциативного массива, в нем можно выделить три основные операции, а именно вставку, удаление и поиск ключа. Как и многие деревья, нагруженное дерево обладает свойством самоподобия, то есть любое его поддерево также является полноценным нагруженным деревом. Легко заметить, что все ключи в таком поддереве имеют общий префикс, (откуда и пошло название «префиксное дерево») а значит можно выделить специфичную для этого дерева операцию — получение всех ключей дерева с заданным префиксом за время O(|Prefix|).
Поиск ключа
Как уже было сказано, ключ, соответствующий узлу — конкатенация меток узлов, содержащихся в пути от корня к данному узлу. Из этого свойства естественным образом следует алгоритм поиска ключа (как, впрочем, и алгоритмы добавления и удаления).
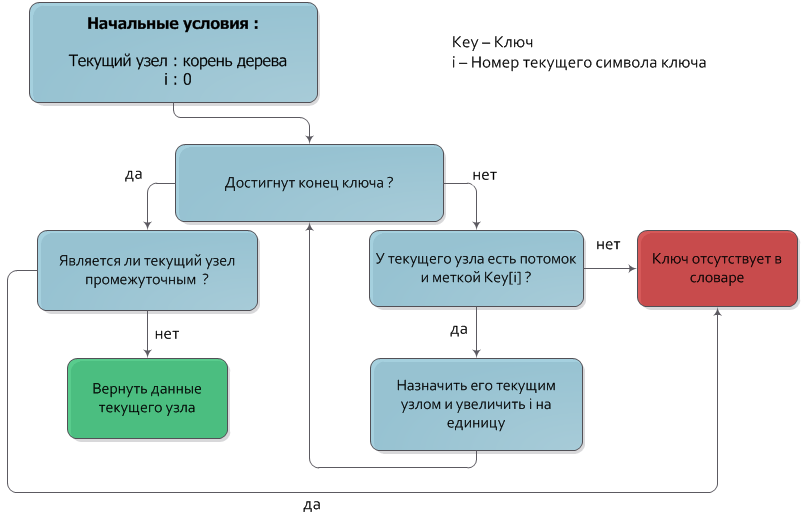
Пусть дан ключ Key, который необходимо найти в дереве. Будем спускаться из корня дерева на нижние уровни, каждый раз переходя в узел, чья метка совпадает с очередным символом ключа. После того как обработаны все символы ключа, узел, в котором остановился спуск и будет искомым узлом. Если в процессе спуска не нашлось узла с меткой, соответствующей очередному символу ключа, или спуск остановился на промежуточной вершине (вершине, не имеющей значения), то искомый ключ отсутствует в дереве.
Временная сложность этого алгоритма, очевидно, равна О(|Key|).
Более подробно алгоритм показан на блок-схеме:
Вставка
Алгоритм добавления ключа в дерево очень похож на алгоритм поиска.
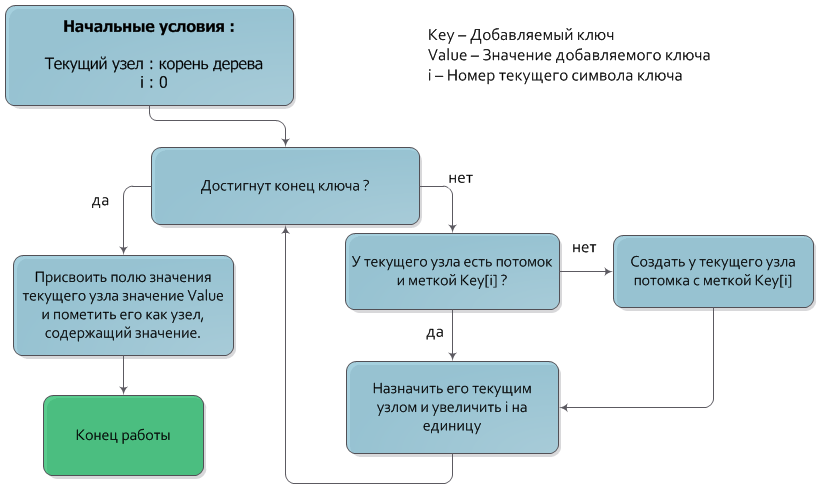
Пусть дана пара из ключа Key и значения Value, которую нужно добавить. Как и в алгоритме поиска ключа, будем спускаться из корня дерева на нижние уровни, каждый раз переходя в узел, чья метка совпадает с очередным символом ключа. После того как обработаны все символы ключа, узел, в котором остановился спуск и будет узлом, которому должно быть присвоено значение Value (также, разумеется, узел должен быть помечен как имеющий значение). Если в процессе спуска отсутствует узел с меткой, соответствующей очередному символу ключа, то следует создать новый промежуточный узел с нужной меткой и назначить его потомком текущего.
Временная сложность добавления ключа — О(|Key|).
Иллюстрация алгоритма на блок-схеме:
Удаление
Удаление ключа также реализуется очень легко.
Пусть дан ключ Key, который необходимо удалить из дерева. Проведем поиск этого ключа. Если ключ существует в словаре, то зная узел, которому он соответствует, можно просто пометить его как промежуточный, сделав его «невидимым» для последующих поисков.
После этого можно подняться от «отключенного» узла к корню, попутно удаляя все узлы которые являются листьями, однако экономия памяти в данном случае не существенна, а для эффективного определения того, является ли узел листом потребуется вводить дополнительную характеристику узла.
Временная оценка алгоритма удаления — знакомое уже О(|Key|).
Требовательность к ресурсам
Нагруженное дерево по показателям потребления памяти/процессорного времени не уступает хэш-таблицам и сбалансированным деревьям, а иногда и превосходит их по этим параметрам.
Процессорное время
Сложность операций вставки, удаления и поиска — O(|Key|). Хотя сбалансированные деревья и выполняют эти операции за O(ln(n)) но в этой асимптотике скрыто время, необходимое для сравнения ключей, которое, в общем случае, составляет O(|Key|). С хэш-таблицами ситуация аналогична — хоть время доступа и составляет О(1+a), но взятие хэша (если он не предвычислен заранее, разумеется) занимает O(|Key|).
Графики со сравнением производительности нагруженных деревьев, хэш-таблиц и красно-черных деревьев можно посмотреть в английской википедии.
Память
По потреблению памяти нагруженное дерево часто выигрывает у хэш-таблиц и сбалансированных деревьев. Это связано с тем что у множества ключей в нагруженном дереве совпадают префиксы, и вместе с ними память которую они используют. Также, в отличии от сбалансированных деревьев, в нагруженном дереве нет необходимости хранить ключ в каждом узле.
Оптимизации
- Сжатие. Сжатое нагруженное дерево получается из обычного удалением промежуточных узлов, которые ведут к единственному не промежуточному узлу. Например, цепочка промежуточных узлов с метками a, b, c заменяется на один узел с меткой abc.
- Patricia. Patricia нагруженное дерево получается из сжатого (или обычного) удалением промежуточных узлов, которые имеют одного ребенка.
Зачем все это нужно?
Собственно, область применения нагруженных деревьев огромна — их можно применять везде где требуется реализация интерфейса ассоциативного массива. Особенно нагруженные деревья удобны для реализации словарей, спеллчекеров и прочих Т9 — то есть в задачах, где необходимо быстро получать наборы ключей с заданным префиксом. Также нагруженное дерево использует в своей работе небезизвестный алгоритм Ахо — Корасик.
Вот собственно и все. Надеюсь, читателю было интересно узнать об этой замечательной структуре данных, незаслуженно редко упоминаемой на Хабре.
Источник
Префиксное дерево (trie)
В этой статье обсудим такую структуру данных, как «префиксное дерево» (оно же нагруженное дерево, бор, trie, prefix tree). Кратко рассмотрим основы и реализуем наиболее важные операции: вставку, поиск по ключу и префиксный поиск.
2. Что такое префиксное дерево?
Trie или префиксное дерево — это особый вид дерева поиска, в котором для ключей узлов обычно используются строки.
Префиксные деревья могут использоваться, например, для реализации множеств и ассоциативных массивов, но по-настоящему они проявляют себя при обходе и поиске ключей, начинающихся с определенного префикса.
По этой причине они часто используются для реализации автодополнения.
3. Структура префиксного дерева
В базовой реализации каждый узел дерева содержит один символ и указатели на дочерние узлы. Ключ узла не хранится в явном виде — он вычисляется как путь от корня до узла.
Выглядит это следующим образом:
Для пометки узлов, в которых содержатся действительные ключи, используется булевый флаг. Кроме того, узлы могут содержать указатель на произвольные данные, например, при реализации ассоциативного массива.
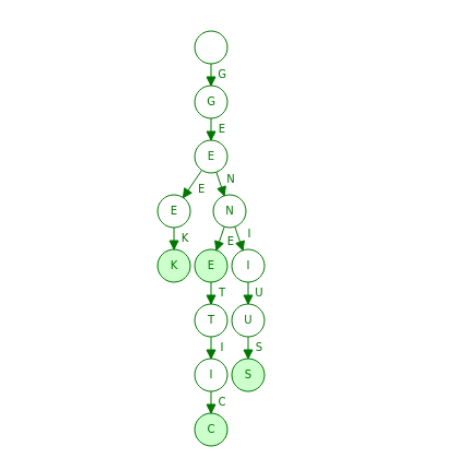
На рисунке показано дерево с ключами: «geek», «genius», «gene» и «genetic». Закрашенные узлы представляют собой допустимые ключи. Структура дерева подразумевает, что все листовые узлы будут допустимыми ключами, но промежуточные узлы необходимо помечать отдельно.
4. Вставка
Поиск места для вставки элемента мы начинаем с корневого узла и идем по дереву вниз, создавая узлы, если они отсутствуют. После создания необходимых узлов устанавливаем флаг действительного ключа для последнего из них.
Например, слово «gene» уже содержится в дереве, и нам надо добавить «genetic»:
- идем по пути «gene»;
- создаем дополнительные узлы для «t», «i» и «c»;
- помечаем последний узел «c» как допустимый ключ.
Но если «genetic» уже есть в дереве, а мы вставляем «gene», то не нужно будет добавлять какой-либо новый узел в дерево.
Единственное действие, которое нужно будет выполнить — пометить конечный узел как допустимый ключ:
5. Поиск
Поиск используется для проверки наличия определенного ключа в дереве, а при реализации ассоциативного массива — для возврата данных, связанных с ключом.
Рассмотрим алгоритм поиска:
Поиск очень похож на вставку, но на этот раз отсутствие ключа означает отсутствие искомого значения. Если мы нашли путь, соответствующий искомому значению, то нам остается лишь проверить действительный ли это ключ.
Обратите внимание, что как в алгоритме вставки, так и в алгоритме поиска нам не нужно было обходить дерево, используя, например, поиск в глубину или в ширину. Это не требовалось, потому что путь, по которому мы должны следовать, непосредственно содержится во входных данных.
6. Поиск по префиксу
Мы рассмотрели основные операции над префиксным деревом. Теперь пришло время поговорить о том, где префиксное дерево наиболее эффективно — поиск слов с заданным префиксом.
- найдем путь для префикса «P», начиная с корня;
- начиная с последнего узла пути «L» вычислим всех потомков «L», которые являются допустимыми ключами;
- вернем найденные узлы.
Вот как это выглядит на практике:
7. Выводы
В этой статье мы познакомились с префиксным деревом и узнали, как реализовать основные операции: вставка, поиск, а также поиск по префиксу.
Дерево отрезков — это структура данных, которая позволяет алгоритмически просто и логарифмически быстро находить сумму элементов массива на заданном отрезке. Приглашаем на открытый бесплатный урок, на котором мы рассмотрим идею дерева отрезков, узнаем, как его строить, обновлять и быстро O(log n) вычислять сумму чисел любого отрезка данного массива. Алгоритм очень простой и экономный: нужно O(n) памяти. Регистрация для всех желающих доступна по ссылке.
Источник