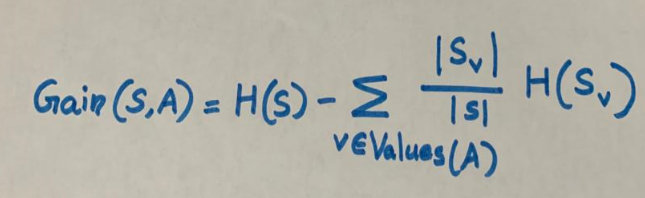Пример обучения дерева решений

Оптимизация производительности дерева решений

Как вы можете видеть выше, дерево слишком обширно и не так точно. Это дерево также требует времени, поэтому для лучших результатов нам нужно оптимизировать дерево путем настройки параметра. Здесь я объясню только важный параметр Алгоритма дерева решений, для его настройки потребуется новый пост в блоге. Если вы посмотрите на параметры DecisionTreeClassifier может взять, вы можете быть удивлены, давайте посмотрим на некоторые из них.

критерий:Этот параметр определяет, как будет измеряться степень загрязнения. Значением по умолчанию является «Джини», но вы также можете использовать «энтропию» в качестве метрики для примесей.

разветвитель:Вот как дерево решений ищет функции для разделения. Значение по умолчанию установлено на «лучший». То есть для каждого узла алгоритм учитывает все функции и выбирает наилучшее разбиение. Если вы решите установить параметр разделителя на «случайный», то будет рассматриваться случайное подмножество объектов. Разделение будет затем выполнено наилучшей функцией в случайном подмножестве. Размер случайного подмножества определяется параметром max_features. Это частично, где Случайный Лес получает свое имя.

Максимальная глубина:Это определяет максимальную глубину дерева. В нашем случае мы используем глубину два, чтобы сделать наше дерево решений. По умолчанию установлено значение none. Это часто приводит к переопределенным деревьям решений. Параметр глубины является одним из способов, которыми мы можем упорядочить дерево или ограничить его рост, чтобы предотвратитьнад-фитинга,

min_samples_split:Минимальное количество выборок, которое должен содержать узел, чтобы рассмотреть расщепление. Значение по умолчанию равно двум. Вы можете использовать этот параметр, чтобы упорядочить ваше дерево.

min_samples_leaf:Минимальное количество выборок необходимо считать листовым узлом. Значение по умолчанию установлено в единицу. Используйте этот параметр, чтобы ограничить рост дерева.

max_features:Количество функций, которые следует учитывать при поиске лучшего разделения. Если это значение не установлено, дерево решений будет учитывать все функции, доступные для наилучшего разделения. В зависимости от вашего приложения, часто бывает полезно настроить этот параметр.

В целях синтаксиса, давайте установим некоторые из этих параметров:

Setting parameterstree = DecisionTreeClassifier(criterion = "entropy", splitter = "random", max_depth = 2, min_samples_split = 5,min_samples_leaf = 2, max_features = 2).fit(X,y)

Дополнительно: переоснащение и недостаточное оснащение

На практике дерево нередко имеет 10 разбиений между верхним уровнем (все данные) и листом. По мере того как дерево становится глубже, набор данных разбивается на листья с меньшим количеством данных. Если у дерева было только 1 разбиение, оно делит данные на 2 группы. Если каждая группа будет разделена снова, мы получим 4 группы данных. Разделение каждого из них снова создаст 8 групп. Если мы продолжим удваивать количество групп, добавляя больше разбиений на каждом уровне, к моменту перехода на 10-й уровень у нас будет 210 210 групп данных. Это 1024 листа.

Когда мы делим данные между многими листами, у нас также меньше данных на каждом листе. Листья с очень небольшим количеством данных сделают прогнозы, которые достаточно близки к фактическим значениям этих домов, но они могут сделать очень ненадежные прогнозы для новых данных (потому что каждое предсказание основано только на нескольких данных).

Это явление называетсяпереобучениягде модель почти полностью соответствует обучающим данным, но плохо проверяет и другие новые данные. С другой стороны, если мы сделаем наше дерево очень поверхностным, оно не разделит данные на очень четкие группы.

В крайнем случае, если дерево делит данные только на 2 или 4, каждая группа по-прежнему имеет широкий спектр данных. Результирующие прогнозы могут быть далеки от большинства данных, даже в данных обучения (и по той же причине они будут плохими в валидации). Когда модель не может зафиксировать важные различия и закономерности в данных, поэтому она плохо работает даже в обучающих данных, это называетсяunderfitting,

Поскольку мы заботимся о точности новых данных, которые мы оцениваем на основе наших данных валидации, мы хотим найти точку отсчета между недостаточным и избыточным соответствием Визуально нам нужна нижняя точка (красной) кривой проверки на изображении, показанном ниже.

Это все, ребята. Счастливого обучения . 🙂

Источник

Как разобраться в дереве принятия решений и сделать его на Python

Совсем скоро, 20 ноября, у нас стартует новый поток «Математика и Machine Learning для Data Science», и в преддверии этого мы делимся с вами полезным переводом с подробным, иллюстрированным объяснением дерева решений, разъяснением энтропии дерева решений с формулами и простыми примерами, вводом понятия «информационный выигрыш», которое игнорируется большинством умозрительно-простых туториалов. Статья рассчитана на любящих математику новичков, которые хотят больше разобраться в работе дерева принятия решений. Для полной ясности взят совсем маленький набор данных. В конце статьи — ссылка на код на Github.

Дерево решений — тип контролируемого машинного обучения, который в основном используется в задачах классификации. Дерево решений само по себе — это в основном жадное, нисходящее, рекурсивное разбиение. «Жадное», потому что на каждом шагу выбирается лучшее разбиение. «Сверху вниз» — потому что мы начинаем с корневого узла, который содержит все записи, а затем делается разбиение.

Корневой узел — самый верхний узел в дереве решений называется корневой узел.
Узел принятия решения — подузел, который разделяется на дополнительные подузлы, известен как узел принятия решения.

Лист/терминальный узел — узел, который не разделяется на другие узлы, называется терминальный узел, или лист.

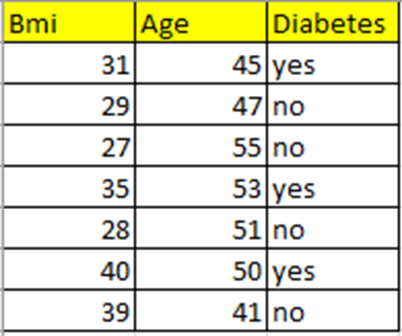
Набор данных

Я взяла совсем маленький набор данных, содержащий индекс массы тела (BMI), возраст (Age) и целевую переменную Diabetes (диабет). Давайте спрогнозируем, будет у человека данного возраста и индекса массы тела диабет или нет.

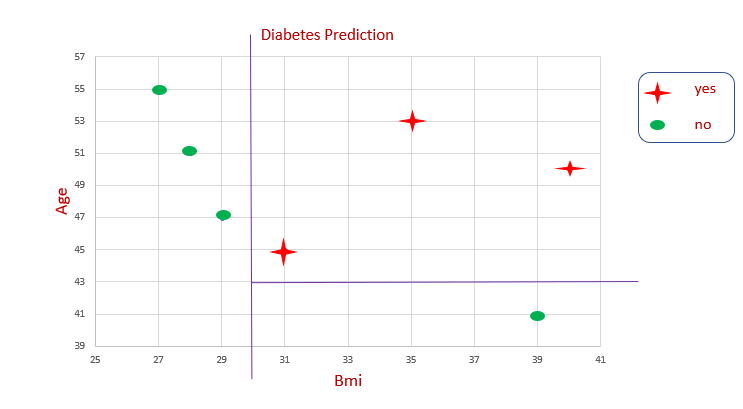
Представление набора данных

На графике невозможно провести какую-то прямую, чтобы определить границу принятия решения. Снова и снова мы разделяем данные, чтобы получить границу решения. Так работает алгоритм дерева решений.

Вот так в дереве решений происходит разбиение.

Важные теоретические определения

Энтропия

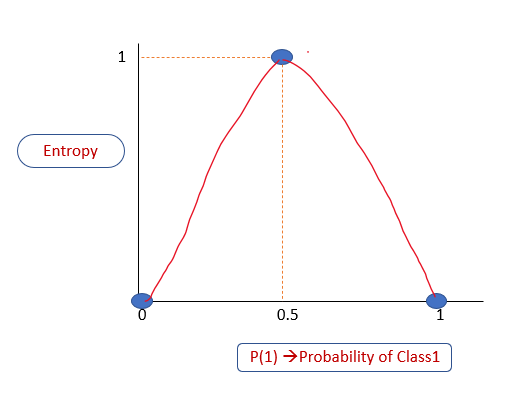
Энтропия — это мера случайности или неопределенности. Уровень энтропии колеблется от 0 до 1 . Когда энтропия равна 0, это означает, что подмножество чистое, то есть в нем нет случайных элементов. Когда энтропия равна 1, это означает высокую степень случайности. Энтропия обозначается символами H(S).

Формула энтропии

Энтропия вычисляется так: -(p(0) * log(P(0)) + p(1) * log(P(1)))

Связь между энтропией и вероятностью

Когда энтропия равна 0, это означает, что подмножество «чистое», то есть в нем нет энтропии: либо все «да», либо все голоса «нет». Когда она равна 1, то это означает высокую степень случайности. Построим график вероятности P(1) вероятности принадлежности к классу 1 в зависимости от энтропии. Из объяснения выше мы знаем, что:

Если P(1) равно 0, то энтропия равна 0
Если P(1) равно 1, то энтропия равна 0
Если P(1) равно 0,5, то энтропия равна 1

Уровень энтропии всегда находится в диапазоне от 0 до 1.

Информационный выигрыш

Информационный выигрыш для разбиения рассчитывается путем вычитания взвешенных энтропий каждой ветви из исходной энтропии. Используем его для принятия решения о порядке расположения атрибутов в узлах дерева решений.

Как работает дерево решений

В нашем наборе данных два атрибута, BMI и Age. В базе данных семь записей. Построим дерево решений для нашего набора данных.

1. Корневой узел

В дереве решений начнем с корневого узла. Возьмем все записи (в нашем наборе данных их семь) в качестве обучающих выборок.

В корневом узле наблюдаем три голоса за и четыре против.
Вероятность принадлежности к классу 0 равна 4/7. Четыре из семи записей принадлежат к классу 0.
P(0) = 4/7
Вероятность принадлежности к классу 1 равна 3/7. То есть три из семи записей принадлежат классу 1.
P(1) = 3/7.

Вычисляем энтропию корневого узла:

2. Как происходит разбиение?

У нас есть два атрибута — BMI и Age. Как на основе этих атрибутов происходит разбиение? Как проверить эффективность разбиения?

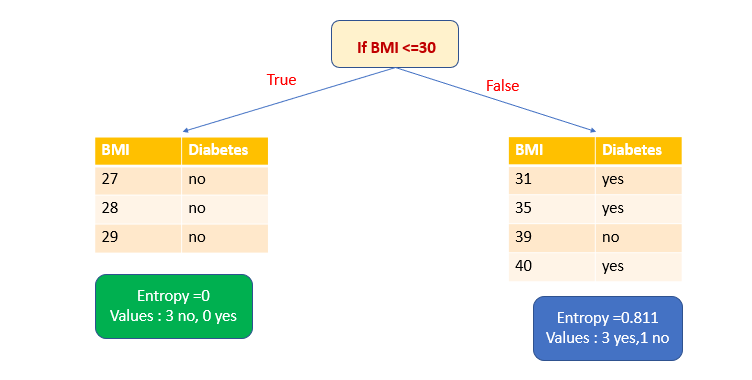
1. При выборе атрибута BMI в качестве переменной разделения и ≤30 в качестве точки разделения мы получим одно чистое подмножество.

Точки разбиения рассматриваются для каждой точки набора данных. Таким образом, если точки данных уникальны, то для n точек данных будет n-1 точек разбиения. То есть в зависимости от выбранных точки и переменной разбиения мы получаем высокий информационный выигрыш и выбираем разделение с этим выигрышем. В большом наборе данных принято считать только точки разделения при определенных процентах распределения значений: 10, 20, 30%. У нас набор данных небольшой, поэтому, видя все точки разделения данных, я выбрала в качестве точки разделения значения ≤30.

Энтропия чистого подмножества равна нулю. Теперь рассчитаем энтропию другого подмножества. Здесь у нас три голоса за и один против.

Чтобы решить, какой атрибут выбрать для разбиения, нужно вычислить информационный выигрыш.

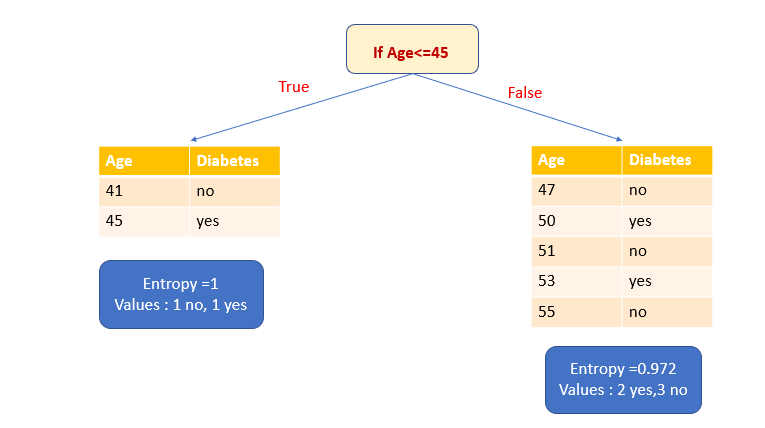
2. Выберем атрибут Age в качестве переменной разбиения и ≤45 в качестве точки разбиения.

Давайте сначала вычислим энтропию подмножества True. У него есть одно да и одно нет. Это высокий уровень неопределенности. Энтропия равна 1. Теперь рассчитаем энтропию подмножества False. В нем два голоса за и три против.

3. Рассчитаем информационный выигрыш.

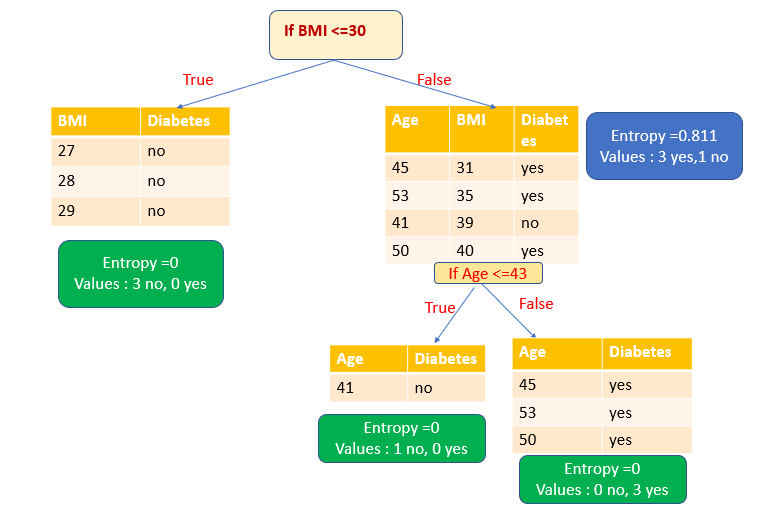
Мы должны выбрать атрибут, имеющий высокий информационный выигрыш. В нашем примере такую ценность имеет только атрибут BMI. Таким образом, атрибут BMI выбирается в качестве переменной разбиения. После разбиения по атрибуту BMI мы получаем одно чистое подмножество (листовой узел) и одно нечистое подмножество. Снова разделим это нечистое подмножество на основе атрибута Age. Теперь у нас есть два чистых подмножества (листовой узел).

Итак, мы создали дерево решений с чистыми подмножествами.

Напишем это на Python с помощью sklearn

1. Импортируем библиотеки.

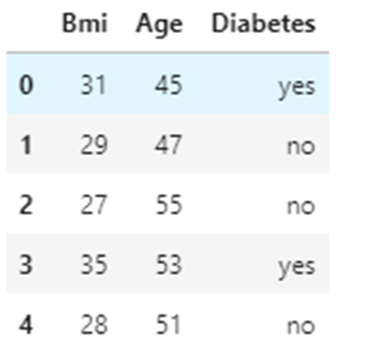
import numpy as np import pandas as pd import matplotlib.pyplot as plt import seaborn as sns 

2. Загрузим данные.

df=pd.read_csv("Diabetes1.csv") df.head() 

3. Разделим переменные на x и y.

Атрибуты BMI и Age принимаются за x.
Атрибут Diabetes (целевая переменная) принимается за y.

x=df.iloc[. 2] y=df.iloc[:,2:] x.head(3) 

4. Построим модель с помощью sklearn

from sklearn import tree model=tree.DecisionTreeClassifier(criterion="entropy") model.fit(x,y) 

Вывод: DecisionTreeClassifier (criterion=«entropy»)

5. Оценка модели

Вывод: 1.0 . Мы взяли очень маленький набор данных, поэтому оценка равна 1.

6. Прогнозирование с помощью модели

Давайте предскажем, будет ли диабет у человека 47 лет с ИМТ 29. Напомню, что эти данные есть в нашем наборе данных.

Вывод: array([‘no’], dtype=object)
Прогноз — нет, такой же, как и в наборе данных. Теперь спрогнозируем, будет ли диабет у человека 47 лет с индексом массы тела 45. Отмечу, что этих данных в нашем наборе нет.

Вывод: array([‘yes’], dtype=object)

7. Визуализация модели:

Код и набор данных из этой статьи доступны на GitHub.

Приходите изучать математику к нам на курс «Математика и Machine Learning для Data Science» а промокод HABR, добавит 10 % к скидке на баннере.

Рекомендуемые статьи

Источник