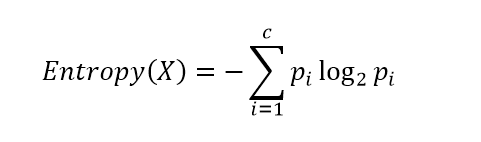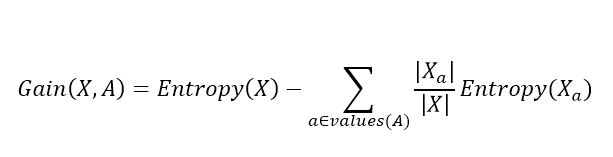Дерево решений
Для построения дерева решений не существует универсального набора символов, но чаще всего квадраты (□) используются для представления «решений», а круги (○) для представления «результатов». Поэтому я буду использовать в своей статье именно эти символы.
Дерево решений и задача, требующая многошагового принятия решений
Дерево решений – это представление задачи в виде диаграммы, отражающей варианты действий, которые могут быть предприняты в каждой конкретной ситуации, а также возможные исходы (результаты) каждого действия. Такой подход особенно полезен, когда необходимо принять ряд последовательных решений и (или) когда на каждом этапе процесса принятия решения могут возникать множественные исходы.
Например, если рассматривается вопрос, стоит ли расширять бизнес, решение может зависеть более чем от одной переменной.
Например, может существовать неопределенность как в отношении объема продаж, так и величины затрат. Более того, значение некоторых переменных может зависеть от значения других переменных: например, если будет продано 100,000 единиц продукта, себестоимость единицы продукта составит $4, но если будет продано 120,000 единиц, себестоимость единицы снизится до $3.80. Таким образом, возможны различные исходы ситуации, при этом некоторые из них будут зависеть от предыдущих исходов. Дерево решений представляет собой полезный метод разделения сложной задачи на более мелкие и более управляемые подзадачи.
Решение задачи при помощи дерева решений осуществляется в два этапа. Первый этап включает построение дерева решений с указанием всех возможных исходов (финансовых результатов) и их вероятностей. Следует помнить, что при принятии решений нужно опираться на принцип релевантных затрат, т. е. использовать только релевантные затраты и выручку. Второй этап включает оценку и формулировку рекомендаций. Принятие решения осуществляется путем последовательного расчета ожидаемых значений исходов в обратном порядке от конца к началу (справа налево). После этого формируются рекомендации для руководства по выбору оптимального образа действий.
Построение дерева решений
Дерево решений всегда следует строить слева направо. Выше я упоминал «решения» и «исходы». Точки принятия решений представляют собой варианты альтернативных действий, то есть возможные выборы. Вы принимаете решение пойти либо этим, либо другим путем. Исходы (результаты решений) от вас не зависят. Они зависят от внешней среды, например, от клиентов, поставщиков или состояния экономики в целом. Как из точек принятия решений, так и из точек исходов выходят «ветви» дерева. Если существует, например, два возможный варианта действий, из точки принятия решения будут выходить две ветви, и если существует два возможных исхода (например, хороший и плохой), то из точки исхода тоже будут выходить две ветви. Поскольку дерево решений является инструментом оценки различных вариантов действий, то все деревья решений должны начинаться с точки принятия решения, которая графически представляется квадратом.
Пример простого дерева решений показан ниже. Из рисунка видно, что лицо, принимающее решение, может выбрать из двух вариантов, поскольку из точки
принятия решения выходит две ветви. Исход одного из вариантов действий, представленного верхней ветвью, точно известен, поскольку на этой ветви нет никаких точек возможных исходов. Но на нижней ветви есть круг, который показывает, что в результате данного решения возможны два исхода, поэтому из него исходят две ветви. На каждой из этих двух ветвей тоже имеется по кругу, из которых, в свою очередь, тоже выходят по две ветви. Это значит, что для каждого из упомянутых возможных исходов имеется два варианта развития ситуации, и каждый из вариантов имеет свой исход. Возможно, первые два исхода представляют собой различные уровни дохода в случае осуществления определенной инвестиции, а второй ряд исходов — различные варианты переменных затрат для каждого уровня доходов.
После построения основы дерева, как показано выше, необходимо указать финансовые значения исходов и их вероятности. Важно помнить, что вероятности, указанные для ветвей, исходящих из одной точки, в сумме должны давать 100%, иначе это будет означать, что вы не указали на диаграмме какой-либо результат, или допустили ошибку в расчетах. Пример приведен ниже в статье.
После построение дерева решений необходимо оценить решение.
Оценка решения
Дерево решений оценивается справа налево, т. е. в направлении, обратном тому, которое использовалось для построения дерева решений. Для того, чтобы осуществить оценку, вы должны предпринять следующие шаги:
- Подпишите все точки принятия решений и исходов, т.е. все квадраты и круги. Начните с тех, которые расположены в самой правой части диаграммы, сверху вниз, и затем перемещайтесь влево до самого левого края диаграммы.
- Последовательно рассчитайте ожидаемые значения всех исходов, двигаясь справа налево, используя финансовые показатели исходов и их вероятности.
Наконец, выберите вариант, который обеспечивает максимальное ожидаемое значение исхода и подготовьте рекомендации для руководства.
Важно помнить, что использование ожидаемых значений для принятия решения имеет свои недостатки. Ожидаемое значение – это средневзвешенное значение исходов решения в долгосрочной перспективе, если бы это решение принималось много раз.
Таким образом, если мы принимаем однократное решение, то фактический результат
быть далек от ожидаемого значения, поэтому данный метод нельзя назвать очень точным. Кроме того, рассчитать точные вероятности довольно сложно, поскольку конкретная рассматриваемая ситуация могла никогда не случаться в прошлом.
Метод ожидаемого значения при принятии решений полезен тогда, когда инвестор имеет нейтральное отношение к риску. Такой инвестор не принимает на себя чрезмерные риски, но и не избегает их. Если отношение к риску лица, принимающего решение, неизвестно, то сложно сказать, стоит ли использовать метод ожидаемого значения. Может оказаться более полезным просто рассмотреть наихудший и наилучший сценарии, чтобы создать основу для принятия решения.
Я приведу простой пример использования дерева решений. В целях упрощения считайте, что все цифры являются чистой приведенной стоимостью соответствующего показателя.
Пример 1
Компания принимает решение, стоит ли разрабатывать и запускать новый продукт. Ожидается, что затраты на разработку составят $400,000, при этом вероятность того, продукт окажется успешным, составляет 70%, а вероятность неудачи, соответственно, 30%. Ниже приведена оценка прибыли от продажи продукта, в зависимости от уровня спроса – высокого, среднего или низкого, а также соответствующие каждому уровню вероятности:
Источник
Использование деревьев решений в задачах прогнозной аналитики
В последние десятилетия одними из самых популярных методов решения задач прогнозной аналитики являются методы построения деревьев решений. Эти методы универсальны, используют эффективную процедуру вычислений, позволяют найти достаточно качественное решение задачи. Именно об этих методах я расскажу в данной статье.
Дерево решений
Дерево решений – структура данных, в процессе обхода которой в каждом узле в зависимости от проверяемого условия принимается определенное решение – перемещение по той или иной ветке дерева от корня к «листьевым» (конечным) вершинам. В «листьевой» вершине дерева содержится искомое значение интересующего атрибута. Деревья решений могут оценивать значения категориальных атрибутов (конечное число дискретных значений), а также количественных. В первом случае говорят о задаче классификации – отнесении объекта к одному из «классов», определяемых атрибутом (например, Да/Нет, Хорошо/Удовлетворительно/Плохо и т.д.). Во втором случае говорят о задаче регрессии, то есть об оценке количественной величины.
Мы рассмотрим алгоритм, позволяющий построить такое дерево решений для оценивания и предсказания значений интересующего нас категориального атрибута анализируемого набора данных на основе значений других атрибутов (задача классификации).
Вообще способов построить дерево может быть бесконечно много – атрибуты можно рассматривать в разном порядке, проверять в узлах дерева различные условия, останавливать процесс, используя разные критерии. Но нас интересуют только деревья, которые наиболее точно оценивают значение атрибута, с минимальной ошибкой, а также позволяют выявлять зависимость между атрибутами и успешно выполнять прогнозирование значений атрибутов на новых данных. К сожалению, не существует хороших алгоритмов, позволяющих гарантированно найти такое «оптимальное» дерево (за приемлемое время). Однако существуют достаточно хорошие алгоритмы, которые пытаются построить «почти оптимальное» дерево, выполняя на каждой итерации определенный «локальный» критерий оптимальности в надежде, что получившееся дерево тоже в целом будет «оптимальным». Такие алгоритмы называются «жадными». Именно такой алгоритм мы и рассмотрим.
Алгоритм построения дерева решений
Принцип построения дерева следующий. Дерево строится «сверху вниз» от корня. Начинается процесс с определения, какой атрибут следует выбрать для проверки в корне дерева. Для этого каждый атрибут исследуется на предмет, как хорошо он в одиночку классифицирует набор данных (разделяет на классы по целевому атрибуту). Когда атрибут выбран, для каждого его значения создается ветка дерева, набор данных разделяется в соответствии со значением к каждой ветке, процесс повторяется рекурсивно для каждой ветки. Также следует проверять критерий остановки.
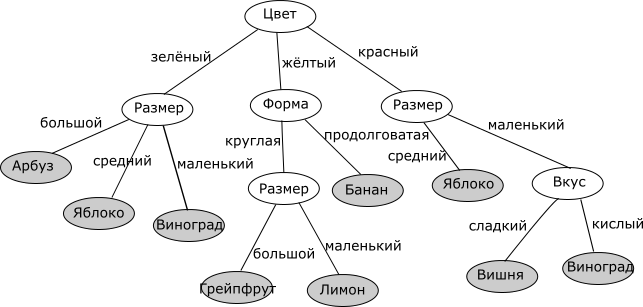
Главный вопрос – как выбирать атрибуты. В соответствии с идеей подхода, когда в концевых узлах дерева (листьях) будет искомый нами класс целевого атрибута, необходимо, чтобы при разбиении набора данных в каждом узле получавшиеся наборы данных были все более однородны в плане значений классов (например, большинство объектов в наборе принадлежало бы к классу Арбуз). И необходимо определить количественный критерий, чтобы оценить однородность разбиения.
Энтропия
Рассмотрим набор вероятностей pi, описывающий вероятность соответствия строки данных в нашем наборе (обозначим его X) классу i. Вычислим следующую величину:
Данная функция представляет собой так называемую энтропию. Энтропия возникла в теории информации и описывает количество информации (в битах), которое необходимо, чтобы закодировать сообщение о принадлежности случайно выбранного объекта (строки) из нашего набора X к одному из классов и передать его получателю. Если класс только один, получателю ничего не нужно передавать, энтропия равна 0 (принимается, что 0log20 = 0). Если все классы равновероятны, то потребуется log2c бит (c – общее количество классов) – максимум функции энтропии.
Далее, для выбора атрибута, для каждого атрибута A вычисляется так называемый прирост информации:
Где values(A) – все принимаемые значения атрибута A, Xa – подмножество набора данных, где A = a, |X| – количество элементов во множестве. Данная величина описывает ожидаемое уменьшение энтропии после разбиения набора данных по выбранному атрибуту. Второе слагаемое – это сумма энтропий для каждого подмножества, взятая со своим весом. Общая разница описывает, как уменьшится энтропия, сколько мы сэкономим бит для кодирования класса случайного объекта из набора X, если мы знаем значения атрибута A и разобьем набор данных на подмножества по данному атрибуту.
Алгоритм выбирает атрибут, соответствующий максимальному значению прироста информации.
Когда атрибут выбран, исходный набор разбивается на подмножества в соответствии с его значениями, исходный атрибут исключается из анализа, процесс повторяется рекурсивно.
Процесс останавливается, когда созданные подмножества стали достаточно однородны (преобладает один класс), а именно когда max(Gain(X,A)) становится меньше некоторого заданного параметра Θ (величина, близкая к 0). Как альтернативный вариант, можно контролировать само множество X, и когда оно стало достаточно мало или стало полностью однородным (только один класс), останавливать процесс.
Жадный алгоритм построения дерева решений
Более структурно алгоритм можно представить следующим образом:
1. Если max(Gain(X,A))
Источник