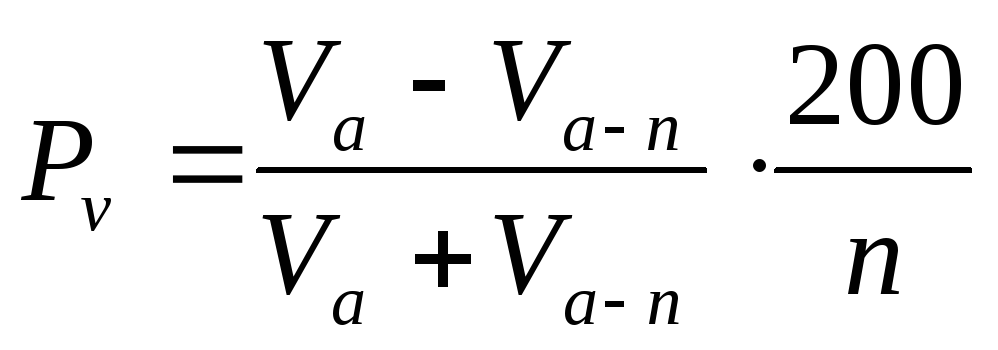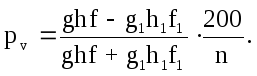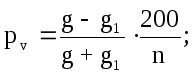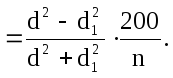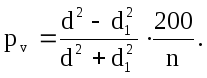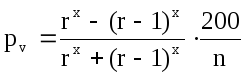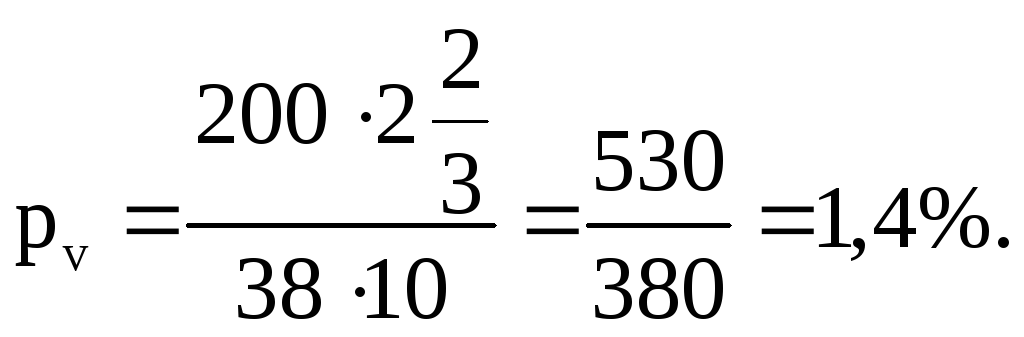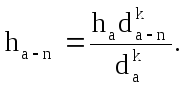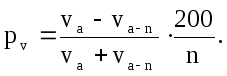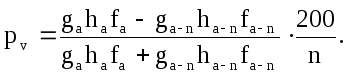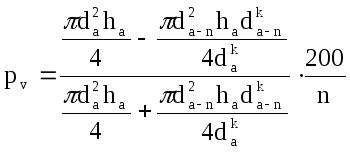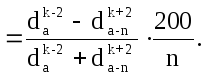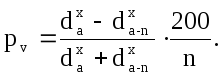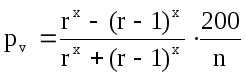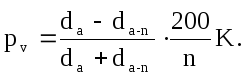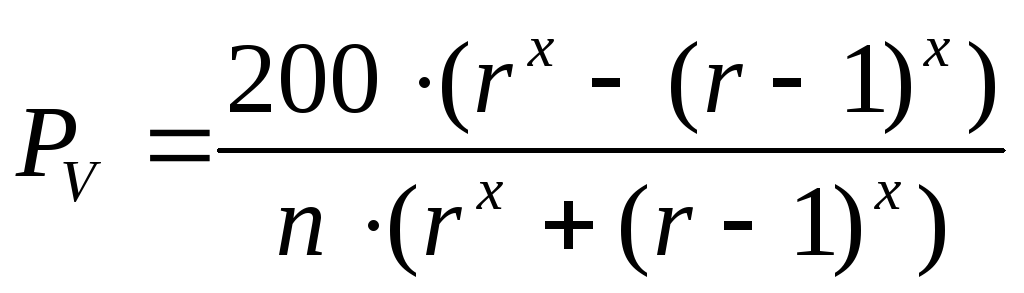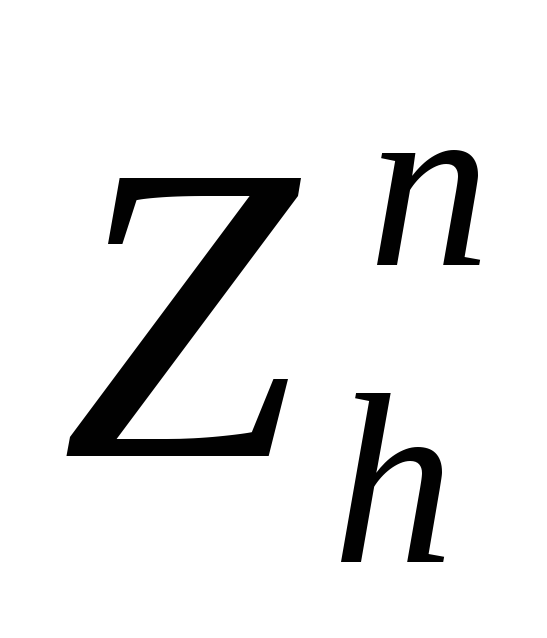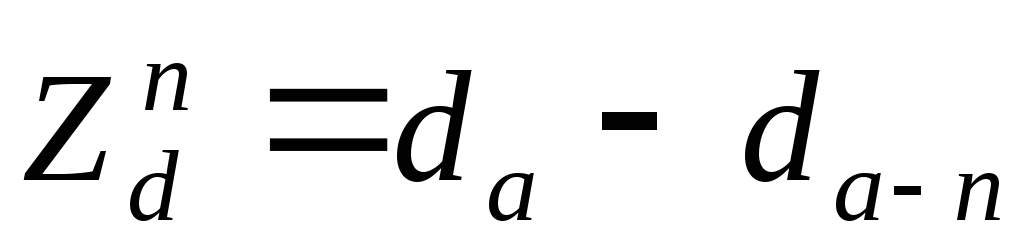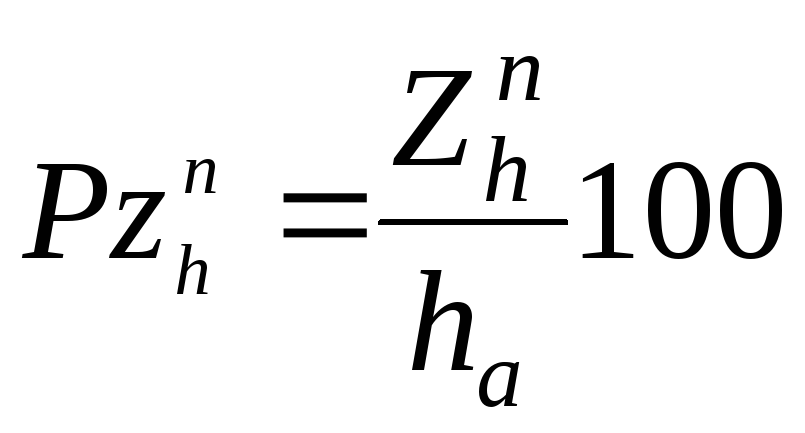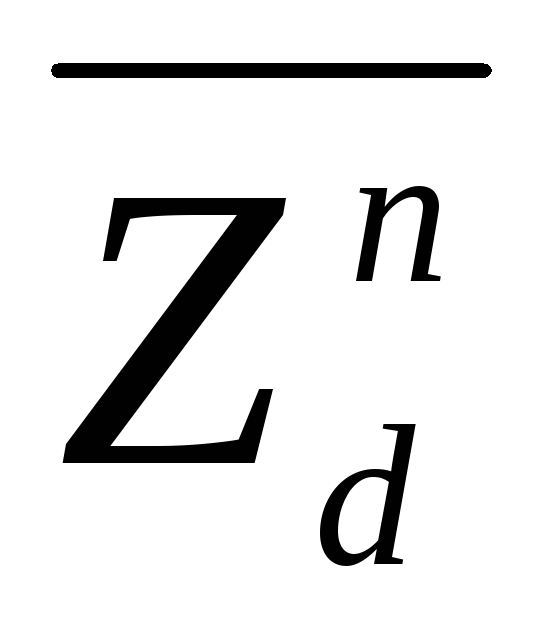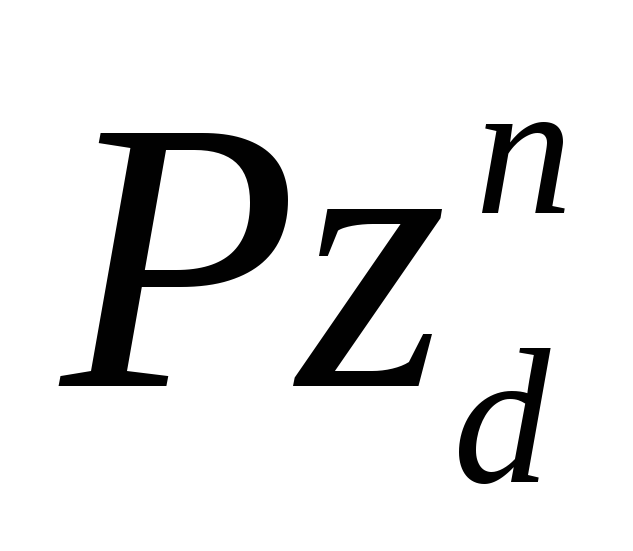Определение прироста у растущих деревьев
Если при определении прироста на срубленном стволе мы встречаемся только с техническими трудностями, то при вычислении прироста растущего дерева нас ожидают методические проблемы. На растущем дереве мы лишены возможности измерить прирост по радиусу на отрезках по высоте дерева. Известную неопределенность вносит и невозможность точного установления прироста по высоте, особенно у деревьев, не образующих мутовки. Поэтому основным измеряемым показателем остается прирост по радиусу или диаметру на доступной нам высоте – 1,3 м. В принципе современные приборы могут обеспечить измерение диаметра и прироста на любой высоте. Но такие приборы дороги, работа с ними идёт очень медленно. Поэтому измерение прироста растущего дерева столь трудоемким способом экономически нецелесообразно. Названный метод может применяться в исключительных случаях
В обычной практике исследований прирост дерева находят через процент прироста. За основу здесь берется вышеприведенная формула Пресслера (14.45).
(14.45)
Объем дерева принимаем равным:
Подставляем эти обозначения в формулу (14.45), получим
Если допустить, что за n лет высота и видовое число остались неизменными, формула, определяющая процент прироста по объему, примет следующий вид:
g = d 2 / 4, g1 = d1 2 / 4,
Для упрощения вычислений введем в формулу относительный диаметр. Относительным диаметром r называется частное от деления диаметра без коры d в данный момент на его прирост Zd за n лет:
Диаметр d1, который имело дерево год назад, обозначим через d-Zd .. В этом случае можно написать
Подставив эти величины в формулу для нахождения процента прироста по объему, выраженного формулой Пресслера, т. е.
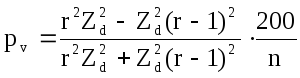
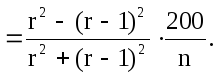
Формула (13.23), определяющая процент прироста по объему в зависимости от величины относительного диаметра, применима для деревьев, у которых прирост в высоту прекратился. Для деревьев, имеющих прирост в высоту, показатели степени в формуле должны соответственно измениться. По мере увеличения роста в высоту показатель степени также увеличивается. По опытным данным, величина его колеблется от 2 до 4.
Исходя из этого, формуле Пресслера, определяющей процент прироста по относительному диаметру, можно придать следующий общий вид:
(14.54)
Исследования показали, что у большей части стволов показатель степени изменяется от 2 до 3,5.
Процент прироста по объему для деревьев, у которых прирост в высоту прекратился и форма ствола осталась неизменной, определяется по формуле
Годичный прирост по диаметру Zd равен удвоенному приросту по радиусу 2Zr. Отсюда получим
Годичный прирост по радиусу Zr представляет не что иное, как ширину одного годичного слоя. Обозначим ее через i. Тогда формула примет такой вид:
При определении ширины годичного слоя подсчитывают число слоев n на последнем сантиметре толщины ствола. Разделив 1 см на число слоев n, получим среднюю ширину годичного слоя 1 / n.
Подставив в формулу (14.55) вместо i величину i / n, получим следующую формулу, определяющую процент текущего прироста:
Эта формула еще в прошлом столетии была предложена немецким лесоводом Шнейдером.
Для деревьев, имеющих прирост по высоте, соответственно интенсивности этого прироста коэффициент, стоящий в числителе формулы, увеличивается. Коэффициент 400 соответствует показателю степени x в формуле (14.54), равному 2. Отсюда на единицу показателя степени приходится коэффициент 400 / 2 = 200.
При определении по выведенной формуле процента прироста для данного дерева надо на этот показатель умножить коэффициент 200. Если диаметр дерева без коры принять 38 см, а число слоев на 1 см радиуса равным 10, процент прироста по объему составит
Коэффициент, стоящий в числителе формулы, изменяется в зависимости от длины кроны и интенсивности роста в высоту. Поэтому рассмотренной формуле следует придать такой общий вид:
При определении прироста необходимо учитывать соотношение между приростом по высоте и по диаметру. Связь этих двух величин проф. Г.М. Турский характеризует таким уравнением:
Показатель степени k характеризует особенности роста деревьев. Если k принять равным единице, формула примет следующий вид:
В этом случае рост дерева в высоту пропорционален росту в толщину. Такой рост называют нормальным. При нормальном росте видовое число остается неизменным и ствол во всех своих частях сохраняет в росте пропорциональность. При k=0 отношение ha-n / ha = 1.
Такой характер роста наблюдается у деревьев, прекративших прирост в высоту, т. е. это старые деревья с отмирающей верхушкой.
Анализируя различные соотношения прироста по высоте и диаметру, можно прийти к выводу, что чем больше k, тем энергичнее рост в высоту в сравнении с ростом в толщину.
На основании уравнения (14.56) находим, что
(14.58)
Нам известно, что процент прироста по объему можно найти по формуле (14.19)
Эту формулу выразим следующим образом:
(14.59)
Допустим, что в течение n лет видовое число ствола остается неизменным. Тогда этой формуле можно придать такой вид:
Подставив x вместо k+2, получим
(14.60)
При замене абсолютных диаметров относительными выше была получена формула (14.61):
(14.61)
Мы уже говорили, что у большей части стволов показатель степени изменяется от 2 до 3 1 /3. Разделив разность между этими числами на пять частей, получаем следующие нормативы для показателя степени: 2; 2,4; 2,7; 3 и 3,3.
Основываясь на правилах сложных процентов и разложив полученные величины в ряды по биному Ньютона, в результате математических преобразований Г.М. Турский получил следующую формулу для определения процента прироста по объему:
(14.63)
Ранее, когда расчеты велись лишь вручную, для упрощения счета составлялись вспомогательные таблицы и номограммы. Н.П. Анучин разработал номограмму, где по величине диаметра дерева и радиального прироста на 1.3 м определяются процент прироста и его абсолютная величина.
Так как вычисления прироста обычно делают в лабораторных условиях, где есть компьютеры, то вспомогательные таблицы и номограммы практически потеряли своё значение.
В силу того, что при нахождении процента прироста растущего дерева используется относительно субъективный показатель (энергия роста в высоту) и при этом пользуются формулами для определения объема, описанный метод имеет невысокую точность: 15-30%.
Прирост отдельного растущего дерева в практике вычисляется очень редко. В практике работы лесхозов обычно не применяются. Гораздо больше значение имеет определение прироста древостоя.
Источник
3) Определение процента текущего прироста деревьев по относительному диаметру (способ Пресслера).
, (44)
где n – период прироста, лет; x – показатель степени, зависит от энергии роста в высоту и протяженности кроны (табл. 12); r – относительный диаметр, определяется как отношение диаметра без коры на высоте 1,3 м в настоящее время к текущему периодическому приросту по диаметру на высоте 1,3 м.
. (45)
Определение группы роста дерева
В зависимости от относительного диаметра и групп роста дерева по Пресслеру по таблицам «Определение процента объемного прироста на стволах растущих деревьев по относительному диаметру» (табл. 3.4 [11]) определяется показатель прироста за n-летний период.
Эту формулу можно использовать для определения процента прироста как растущих, так и срубленных деревьев. Во втором случае величина r устанавливается на половине высоты дерева, которое оно имело n лет назад (). По таблице 3.5 [11]. определяют процент прироста по объему по относительному диаметру.
4) Определение процента объемного прироста по формуле А. В. Тюрина. Особое внимание при этом придается приросту по диаметру благодаря легкости измерения его на стоящем дереве; прирост по высоте и форме hf или остается вне расчета, или учитывается по индивидуальной его величине:
PV = 2Pd + 0,7Ph. (46)
5) Из формулы объема ствола V = ghf (где g – площадь сечения на высоте 1,3 м; h – высота дерева; f – видовое число) следует, что формирование процента объемного прироста PV происходит путем сложения процентов прироста перечисленных компонентов объема, т. е. g, h, f:
PV = Pg + Ph + Pf. (47)
Пример 13. Для модельного дерева, в соответствии с вариантом, диаметр ствола на высоте груди без коры в настоящее время равен da = 29,8 см; диаметр 10 лет тому назад da—n = 26,7 см; ha = 25.3 м; высота 10 лет тому назад ha—n = 22,1 м возраст дерева 65 лет протяженность кроны 35%. Следует вычислить процент текущего прироста по формулам 41, 42, 46, 47 и с помощью таблиц [11].
Прежде всего вычисляем текущий абсолютный периодический по высоте (ф. 37) (или используем ранее вычисленный) :
= 25,3 – 22,1 = 3,2 м.
На основании этого числа определяем энергию роста в высоту (табл. 11) – «хороший». В этом случае по табл. 5 k =1. Подставляя все данные в формулу Г. М. Турского (ф. 41), получаем
При определении процента текущего прироста по способ Шнейдера вычисляем ширину годичного слоя (ф. 43):
i = 3,1/(2·10) = 0,155 см = 1,6 мм
При протяженность кроны менее ½Н и хорошей энергии роста в соответсвтвии с табл. 10 K = 600. В этом случае по ф. 42 вычисляем:
PV = 600·0,155/29,8 = 3,12%
Используя полученные ранее результаты, находим процент текущего прироста по ф. 46 и 47.
Для определения PV с помощью таблиц находим относительный диаметр на высоте 1,3 м. Тогда
По протяженности кроны и энергии роста определяется группа роста дерева (табл. 12) IV, и по таблицам 3.4 и 3.5 [1 ] находим PV за десять лет : 37%, за 1 год он составит 3,7%.
Источник
Задание 5. Определение прироста древесного ствола
5.1. Определение прироста ствола срубленного дерева
Под приростом понимают увеличение размеров и массы дерева за какой-то период времени, обусловленное физиологическими процессами роста и развития. Прирост ствола дерева – это величина изменения его таксационных показателей (d, h, g, V, f ) с возрастом.
Различают два вида прироста: текущий и средний. Каждый из них определяется в абсолютных (см, м, м 3 ) и относительных (%) величинах.
Текущий прирост по диаметру без коры на высоте груди.
Абсолютный текущий периодический прирост по диаметру ствола на высоте 1,3 равен:
. (32)
где da – диаметр ствола без коры, см; da—n – диаметр ствола n лет назад, который определяется путем измерения приростным буравом Пресслера годичного Zr n прироста или средней ширины годичного слоя i:
Для определения средней ширины годичного слоя на стволе (высота 1,3 м) буравом Пресслера берут керн древесины, на котором измеряют ширину n годичных слоев. Средняя ширина годичного слоя вычисляется делением ширины n годичных слоев в милиметрах на период a лет [1, 5, 13].
Абсолютный текущий среднепериодический прирост по диаметру определяется по формуле:
(33)
Относительный текущий периодический прирост по диаметру ствола равен:
. (34)
Абсолютный средний прирост по диаметру ствола :
. (35)
Относительный средний прирост по диаметру ствола :
(36)
Абсолютный текущий периодический прирост по высоте дере-ва :
, (37)
где ha – длина (высота) ствола в момент таксации (a, лет), м; ha – n – длина ствола n лет назад, см.
Длину ствола срубленного дерева ha измеряют металлической рулеткой. Длину ствола n лет назад ha – n у хвойных молодых деревьев определяют по мутовкам. От вершины дерева отсчитывают n мутовок. Длина ствола ha – n измеряется от среза пня до основания n-й мутовки.
Относительный текущий периодический прирост по высоте дерева равен:
. (38)
Абсолютный средний прирост по высоте ствола Zh:
. (39)
Относительный средний прирост по высоте ствола:
. (40)
Аналогичные расчеты проводятся при вычислении среднепериодического и среднего прироста по площади сечения и видовому числу ствола в абсолютных и относительных величинах. Исходные данные для расчетов берут в задании 1.
Пример 12. Диаметр ствола на высоте груди без коры в настоящее время равен da = 29,8 см; диаметр 10 лет тому назад da—n = 26,7 см; возраст дерева 65 лет
Текущий абсолютный периодический прирост (ф. 32) равен
= 29,8 – 26,7 = 3,1 см.
Абсолютный текущий среднепериодический прирост по диаметру определяется по ф. 33:
=3,1/10=0,31 см.
Относительный текущий периодический прирост по диаметру вычисляется в соответствии с ф. 34:
=100%·0,31/29,8 = 1,04 %
Средний прирост определяется (ф. 35)
= 29,8/65 = 0,4 см
Относительный средний прирост в соответствии с ф. 36:
= 100%·0,4/25,8=1,6%
Аналогичным образом вычисляются все виды прироста по высоте, площади сечения и видовому числу дерева.
Источник