Обход дерева¶
После испытания функционала нашего дерева, пришло время расмотреть некоторые дополнительные модели использования этой структуры данных. Их можно разделить по трём способам доступа к узлам дерева. Различие будет состоять в порядке посещения каждого узла. Мы будем называть посещение узлов словом “обход”. Три способа обхода, которые будут рассмотрены, называются обход в прямом порядке, симметричный обход и обход в обратном порядке. Начнём с того, что дадим им более точные определения, а затем рассмотрим несколько примеров, где эти модели будут полезны.
Обход в прямом порядке В этом случае мы сначала посещаем корневой узел, затем рекурсивно обходим в прямом порядке левое поддерево, после чего таким же образом обходим правое. Симметричный обход Сначала мы симметрично обходим левое поддерево, затем посещаем корневой узел, затем — правое поддерево. Обход в обратном порядке Сначала делается рекурсивный обратный обход левого и правого поддеревьев, после чего посещается корневой узел.
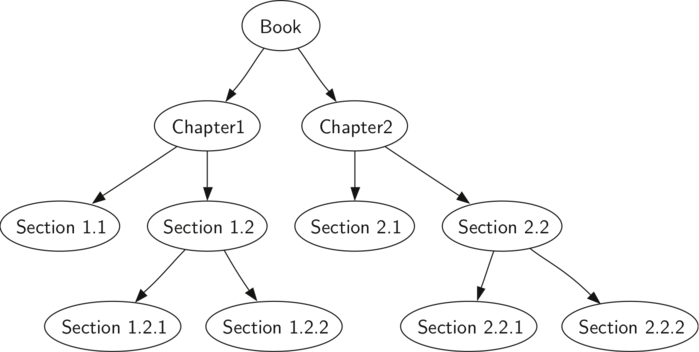
Рассмотрим несколько примеров, иллюстрирующих каждый из этих типов обхода. Первым будет обход в прямом порядке. В качестве примера дерева возьмём эту книгу. Сама по себе она является корнем, чьи потомки — главы. Каждый раздел главы будет уже её потомком, каждый подраздел — потомком раздела и так далее. Рисунок 5 показывает урезанную версию книги (всего две главы). Обратите внимание, что алгоритм обхода будет работать с любым числом потомков, но мы пока сосредоточимся на двоичном дереве.
Рисунок 5: Представление книги в виде дерева
Предположим, вы хотите прочитать эту книгу от начала до конца. Обход в прямом порядке даст вам в точности такую последовательность. Начиная с корня дерева (узел Book), последуем инструкциям прямого обхода. Мы рекурсивно вызовем preorder к левому потомку Book (Chapter1), а потом уже к его левому потомку (Section 1.1). Section 1.1 является листом, так что больше рекурсивные вызовы не нужны. Закончив с ней, поднимемся по дереву вверх до Chapter 1. Нам по-прежнему надо посетить правое поддрево — Section 1.2. Как и раньше, сначала мы пойдём по его левому потомку (1.2.1), а затем посетим узел Section 1.2.2. Закончив с Section 1.2, мы вернёмся к Chapter 1, потом к Book и проделаем аналогичную процедуру для Chapter 2.
Код для описанного обхода дерева на удивление элегантный — в основном благодаря рекурсии. Листинг 2 демонстрирует код прямого обхода двоичного дерева.
Может возникнуть вопрос: в каком виде лучше написать алгоритм вроде обхода в прямом порядке? Должна ли это быть функция, просто использующая дерево как структуру данных, или это будет метод внутри класса “дерево”? В листинге 2 показан вариант с внешней функцией, принимающей двоичное дерево в качестве параметра. В частности, элегантность такой функции заключается в базовом случае — проверке существования дерева. Если её параметр равен None , то она возвращается без выполнения каких-либо действий.
def preorder(tree): if tree: print(tree.getRootVal()) preorder(tree.getLeftChild()) preorder(tree.getRightChild())
Также preorder можно реализовать, как метод класса BinaryTree . Код для этого случая показан в листинге 3. Обратите внимание, что происходит, когда мы перемещаем код “снаружи” “внутрь”. В общем, tree просто заменяется на self . Однако, так же требуется изменить и базовый случай. Внутренний метод проверяет наличие левого и правого потомков до того, как делается рекурсивный вызов preorder .
def preorder(self): print(self.key) if self.leftChild: self.left.preorder() if self.rightChild: self.right.preorder()
Какой из двух способов реализации preorder лучше? Ответ: для данного случая — в виде внешней функции. Причина в том, что вы очень редко хотите просто обойти дерево. В большинстве случаев вам нужно сделать что-то ещё во время использования одной из моделей обхода. Фактически, уже в следующем примере мы увидим, что модель обхода postorder очень близка к коду, который мы писали ранее для вычисления дерева синтаксического разбора. Исходя из изложенного, для оставшихся моделей мы будем писать внешние функции.
Алгоритм обхода postorder показан в листинге 4. Он очень близок к preorder , за исключением того, что мы перемещаем вызов печати в конец функции.
def postorder(tree): if tree != None: postorder(tree.getLeftChild()) postorder(tree.getRightChild()) print(tree.getRootVal())
Мы уже видели распространённое использование обхода в обратном порядке — вычисление дерева синтаксического разбора. Взгляните на листинг 1 ещё раз. Что мы делаем, так это вычисляем левое поддерево, потом правое и собираем их в корне через вызов функции оператора. Предположим, наше двоичное дерево будет хранить только данные для математического выражения. Давайте перепишем функцию вычисления более приближённо к коду postorder из листинга 4 (см. листинг 5).
def postordereval(tree): opers = '+':operator.add, '-':operator.sub, '*':operator.mul, '/':operator.truediv> res1 = None res2 = None if tree: res1 = postordereval(tree.getLeftChild()) res2 = postordereval(tree.getRightChild()) if res1 and res2: return opers[tree.getRootVal()](res1,res2) else: return tree.getRootVal()
Обратите внимание, что код в листинге 4 аналогичен коду из листинга 5, за исключением того, что вместо печати ключей в конце функции, мы их возвращаем. Это позволяет сохранить ответы рекурсивных вызовов в строках 6 и 7. Потом они используются вместе с оператором в строке 9.
Последним рассмотренным в этом разделе обходом будет симметричный обход. В его ходе мы сначала посещаем левое поддерево, затем корень и потом уже правое поддерево. Листинг 6 показывает этот алгоритм в коде. Заметьте: во всех трёх моделях обхода мы просто меняем расположение оператора print по отношению к двум рекурсивным вызовам.
def inorder(tree): if tree != None: inorder(tree.getLeftChild()) print(tree.getRootVal()) inorder(tree.getRightChild())
Если мы применим простой симметричный обход к дереву синтаксического разбора, то получим оригинальное выражение, правда без скобок. Давайте модифицируем базовый алгоритм симметричного обхода, чтобы он позволял восстановить версию выражения с полной расстановкой скобок. Единственное изменение, которое надо внести в базовый шаблон, — это печатать левую скобку до рекурсивного вызова с левым поддеревом и правую скобку после рекурсивного вызова с правым поддеревом. Модифицированный код показан в листинге 7.
def printexp(tree): sVal = "" if tree: sVal = '(' + printexp(tree.getLeftChild()) sVal = sVal + str(tree.getRootVal()) sVal = sVal + printexp(tree.getRightChild())+')' return sVal
Обратите внимание, что функция printexp после реализации помещает скобки вокруг каждого числа. Не то, чтобы это было неправильно, но они здесь просто не нужны. В упражнении в конце этой главы мы попросим вас изменить printexp , чтобы исправить это.
© Copyright 2014 Brad Miller, David Ranum. Created using Sphinx 1.2.3.
Источник
Прямой, обратный и симметричный обход дерева
Обход дерева – систематический порядок перечисления всех узлов дерева в соответствие с некоторым правилом упорядочивания этих узлов. При обходе дерева следует различать левого и всех остальных сыновей. Данную последовательность можно обойти, учитывая упорядочивание слева на право.
- А ВС – прямой.
- ВСА – обратный, сначала сыновья потом родители.
- ВАС – симметричный (внутренний).
Формально процедуру обхода можно записать следующим образом, если
дерево Т нулевое, то список обхода пуст. Если дерево состоит из одного
элемента, то список обхода заносится и обход завершается. Если корень Т имеет Тn, то различают следующие варианты обхода: при прохождение в прямом порядке обхода сначала посещается корень дерева (поддерева), а
затем слева на право посещаются его деревья T1,T2 …Tk, причем к поддереву Tk переход осуществится, только после того, как все дерево T1 будет обойдено аналогичным образом в начале корень, а потом сыновья поддеревья; симметричный обход дерева T начинается с обхода левого дерева T1
после чего посещается родитель T1, дальше слева на право посещается T2 …Tk, каждое из деревьев Ti посещается аналогичны образом; обратный обход T1, T2 …Tk, а затем n каждое из поддеревьев обходится аналогичным образом.
- 5, 1, 2, 11, 6, 12, 7, 8, 9, 4, 3, 10.
- 2, 11, 1, 12, 6, 5, 8, 7, 9, 4, 10, 3.
- 11, 2, 12, 6, 1, 8, 4, 9, 7, 10, 3, 5.
Помеченные деревья или деревья выражений
Помеченное дерево – деревья узлы, которые хранят значения. В дереве выражений, каждый внутренний узел не лист хранит не арифметическую операцию (бинарную), а лист является переменной или константой, т.е. аргументом операции.
( а + в)*(а — с), чтобы вычислить это выражение а, в, +, а, с, -, * получим обратный обход или постфиксное (польскую) представление выражения, который используется при вычисление выражения в нем – P1 P2 Ө, где P1,P2 постфикс соответствующего выражения.
Здесь не требуется скобок для вычисления операций, потому что расставлена как к структуре дерева.
+ а в – а с , Ө P1 P2, префиксная форма запись подвыражения.
а + в * в – с, P1 Ө P2 симметричный (внутренний) инфикс, скобки в данном случае нужны.
Вычислить 5 9 10 * + Перевести из постфикса в префикс 2 4 3 * — 5 4 + +
Пусть E1 и E2 подвыражения арифметического вида E1 Ө E2, причем Е1 соответствие левого поддерева, а Е2 правое поддерево с корнем в узле Ө. Таки образом Ө соответствует арифметической операции бинарного вида, т.е. Е1 и Е2 построен в подобных структурах. Тогда обход этого дерева в прямом порядке, Ө Р1 Р2 соответствует префиксной форме записи арифметического выражения. Здесь Р1 и Р2 префиксные формы записи выражений Е1 и Е2. Скобки в префиксном выражение не требуются, так как всегда можно посмотреть Ө Р1 Р2 слева на право без возврата, чтобы определить самый короткий префикс Р1 как единственный возможный в выражение Р1 Р2 (Ө Р1 Р2 ≡ Р). Аналогично обратный обход записывается в виде Р1 Р2 Ө, где Р1 и Р2 постфиксная форма записи поддеревьев Е1 и Е2, скобки также не требуются, так как с одной стороны двигаясь слева на право в выражениях Р1 и Р2 всегда можно выделить Е1, как самый короткий постфикс. А с другой стороны само дерево выражений, так как сама структура дерева однозначно определяет приоритет операций, а разбирая префиксное или постфиксное выражение можно однозначно реконструировать самом дерево чего нельзя добиться в случае с инфиксной формой записи.
Источник