Python дерево отрезков сумма

Дерево отрезков

Для изучения темы “дерево отрезков” необходимо знать следующие понятия:

Дерево отрезков (Segment Tree) — это динамическая структура данных, используемая для выполнения операций над интервалами и их обновления. Оно поддерживает две операции: обновление элементов (update) в заданном диапазоне и запрос (query) на сумму элементов в заданном диапазоне.

Выполним следующую задачу: у нас есть массив, и мы хотим находить сумму элементов в определенном диапазоне.

Для этой задачи мы можем использовать дерево отрезков. Оно построено как бинарное дерево, где каждый узел представляет интервал, а значение узла — это сумма элементов в этом интервале.

Элемент суммы в дереве отрезков является суммой всех элементов в диапазоне, который он представляет.

Дерево отрезков может быть построено на базе массива чисел. Каждый узел дерева представляет диапазон элементов в массиве и хранит сумму элементов в этом диапазоне.

Реализация различных операций в дереве отрезков по сути зависит от его структуры. Однако, существует несколько операций, которые часто используются в различных задачах:

• Обновление значения в массиве: Эта операция позволяет изменять значение элемента в массиве. Обычно она реализуется с помощью рекурсивного прохода по дереву.
• Запрос на значение: Эта операция позволяет запрашивать значение элемента в массиве. Обычно она также реализуется с помощью рекурсивного прохода по дереву.
• Запрос на сумму: Эта операция позволяет запрашивать сумму значений в массиве на заданном интервале. Она обычно реализуется с помощью рекурсивного прохода по дереву и подсчета суммы

Построение дерева отрезков

Так как дерево бинарное, у каждой вершины будет до двух потомков.

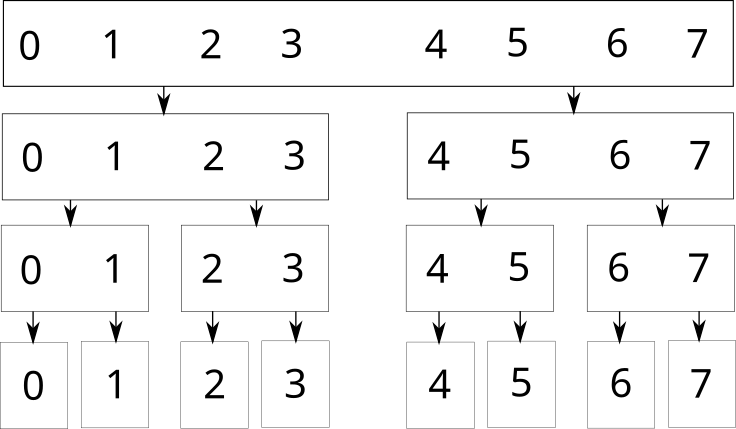
Графически это выглядит следующим образом (для массива из 8 элементов):

В самой верхней вершине зафиксирован отрезок от начала массива до последнго элемента.

Слева — лева половина от родителя ( [0 1 2 3] ). Справа — правая половина () [4 5 6 7] ). И так далее до последнего узла с отрезком из одного элемента.

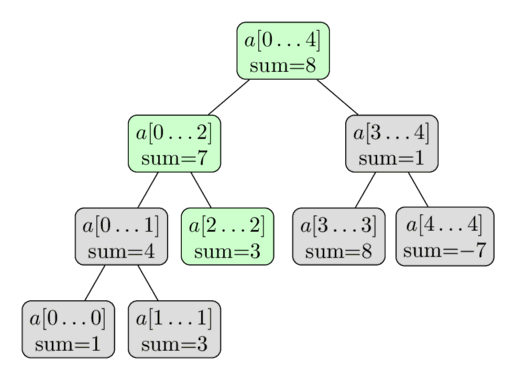
Возьмем массив a = [1, 3, -2, 8, -7] . На его базе построим дерево отрезкови запишем суммы этих отрезков в каждый узел.

Структура такого дерево выглядит следующим образом:

💡 Дерево содержит менее 2n вершин. 2*n-1

Число вершин в худшем случае оценивается суммой $n + \frac + \frac + \frac + \ldots + 1 < 2n$

Отобразим такое дерево как массив:

tree[0] = A[0:4] tree[1] = A[0:2] tree[2] = A[3:4] tree[3] = A[0:1] tree[4] = A[2:2] tree[5] = A[3:3] tree[6] = A[4:4] tree[7] = A[0:0] tree[8] = A[1:1] 

В данном дереве покрыты все вершины.

Имея такую структуру, в значениях вершин можно хранить различные данные, например, сумму отрезка, наименьшее/наибольшее число или другие агрегированные данные на отрезках.

Реализация дерева отрезков на Python

Так как самыми последними вершинами являются отрезки длиной == 1 . То процесс создания начинаем с них, постепенно поднимаясь на уровень выше.

💡 Дерево содержит менее 2n вершин. 💡 Нижняя виршина — длина отрезка равна 1.

def build_tree(array):  n = len(array)  tree = [0] * 2 * n # Дерево содержит менее **2n** вершин.   for i in range(n):  tree[n + i] = a[i] # самые нижние вершины дерева   # добавляем родителей  for i in reversed(range(n)):  tree[i] = tree[2 * i] + tree[2 * i + 1]  print(i, tree)  >> array = [1, 3, -2, 8, -7] >> build_tree(array)   4 [0, 0, 0, 0, 1, 1, 3, -2, 8, -7]  3 [0, 0, 0, 1, 1, 1, 3, -2, 8, -7]  2 [0, 0, 2, 1, 1, 1, 3, -2, 8, -7]  1 [0, 3, 2, 1, 1, 1, 3, -2, 8, -7]  0 [3, 3, 2, 1, 1, 1, 3, -2, 8, -7] 

Подсчет суммы на отрезке:

Функция получает индексы исходного массива.

При создании дерева из изходного массива мы помещали каждый отдельный элемент на новый индекс [n + i] .

💡 Поэтому когда функция принимает индекс, сначала мы найдет самый нижний элемент в дереве. Он расположен в новом массиве по индексу [длина_исходного_массива + index]

# подсчет суммы на отрезке def query_tree(l, r):  global tree, n   sum = 0  l += n # индекс текущего элемента  r += n  while l  r:  if l % 2 == 1: # если индекс нечетный  sum += tree[l]  l += 1  if r % 2 == 0:  sum += tree[r]  r -= 1  l //= 2 # floor division. 8 // 3 = 2  r //= 2  return sum  >> a = [1, 3, -2, 8, -7] >> n = len(a) >> tree = build_tree(a)  >> query_tree(0, 4) # sum([1, 3, -2, 8, -7]) 3 >> query_tree(1, 3) # sum([3, -2, 8]) 9 >> query_tree(4, 4) -7 

Получаем класс SegmentTree :

Функцию суммирования или любую другую можно включить в момент генерации дерева

class SegmentTree:  def __init__(self, a):  self.n = len(a)  self.tree = [0] * 2 * self.n  for i in range(self.n):  self.tree[self.n + i] = a[i]  for i in range(self.n - 1, 0, -1):  self.tree[i] = self.tree[2*i] + self.tree[2*i+1]   def calculate_sum(self, l, r):  sum = 0  l += self.n  r += self.n  while l  r:  if l % 2 == 1:  sum += self.tree[l]  l += 1  if r % 2 == 0:  sum += self.tree[r]  r -= 1  l //= 2  r //= 2  return sum   def find_value(self, l, r):  l += self.n  r += self.n  while l  r:  if r % 2 == 0:  r -= 1  else:  r -= 1  l += 1  return l - self.n 

Шаблон класса Segment Tree

class SegmentTree:  def __init__(self, data, default=0, func=max):  self._default = default  self._func = func  self._len = len(data)  self._size = _size = 1  (self._len - 1).bit_length()   self.data = [default] * (2 * _size)  self.data[_size:_size + self._len] = data  for i in reversed(range(_size)):  self.data[i] = func(self.data[i + i], self.data[i + i + 1])  def __delitem__(self, idx):  self[idx] = self._default  def __getitem__(self, idx):  return self.data[idx + self._size]  def __setitem__(self, idx, value):  idx += self._size  self.data[idx] = value  idx >>= 1  while idx:  self.data[idx] = self._func(self.data[2 * idx], self.data[2 * idx + 1])  idx >>= 1  def __len__(self):  return self._len  def query(self, start, stop):  """func of data[start, stop)"""  start += self._size  stop += self._size  if start==stop:  return self._default  res_left = res_right = self._default  while start  stop:  if start & 1:  res_left = self._func(res_left, self.data[start])  start += 1  if stop & 1:  stop -= 1  res_right = self._func(self.data[stop], res_right)  start >>= 1  stop >>= 1   return self._func(res_left, res_right)  def __repr__(self):  return "SegmentTree( )".format(self.data) 

Метод build_tree строит дерево отрезков, а query позволяет выполнять операции запроса.

Ресурсы

Источник

Дерево отрезков

Дерево отрезков — структура данных, позволяющая выполнять многие операции с отрезками массива за \(O(\log N)\). Дерево отрезков — универсальная структура данных, для которой можно реализовать неограниченный набор операций (иногда за большую сложность: \(O(\log^2 N)\)). Самая простая версия дерева отрезков позволяет находить сумму или минимум на отрезке, и изменять отдельные элементы.

Построение дерева отрезков

Дерево отрезков — полное бинарное дерево, в котором каждая вершина отвечает за некоторый отрезок в массиве. Корень дерева отвечает за весь массив, его две дочерних вершины — за две половины, и так далее. У каждой вершины, отвечающей за отрезок длиной больше \(1\), есть две дочерних вершины, отвечающих за левую и правую половины этого отрезка. Листья дерева отрезков отвечают за отдельные элементы (отрезки длиной \(1\)).

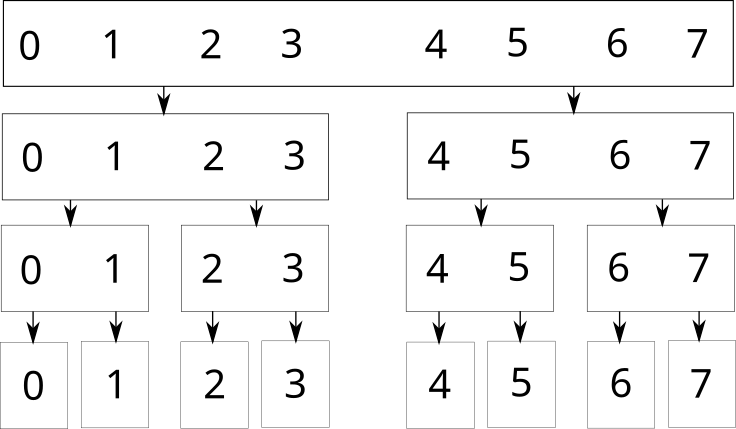
Графически это выглядит следующим образом (для массива из 8 элементов):

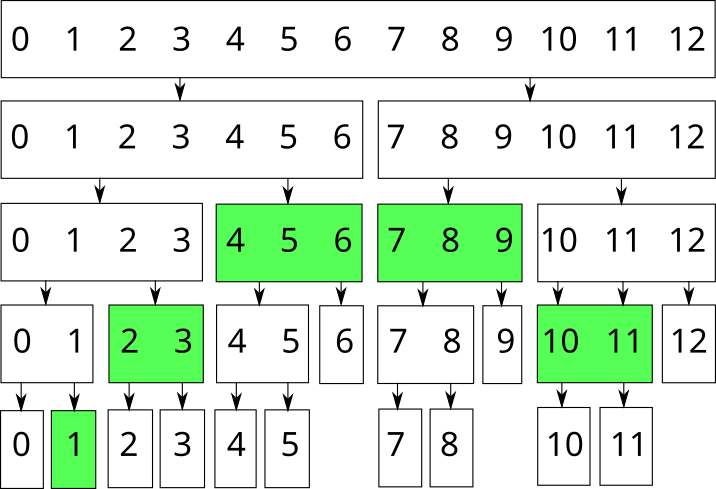
Каждый прямоугольник — вершина дерева отрезков. Если некоторая вершина отвечает за отрезок нечётной длины, то одна из её дочерних вершин будет отвечать за отрезок длиной \(\lceil \rceil\), а другая — за отрезок длиной \(\lfloor \rfloor\). Например, так выглядит дерево отрезков для массива из 13 элементов:

Для массива из \(n\) элементов дерево отрезков имеет около \(2n\) вершин (\(n + + + \ldots\)), а его высота равна порядка \(\log n\).

Главное свойство дерева отрезков, на котором и строятся все алгоритмы работы с ним: любой непрерывный отрезок в массиве из \(n\) элементов можно представить с помощью около \(2 \log n\) вершин в дереве отрезков.

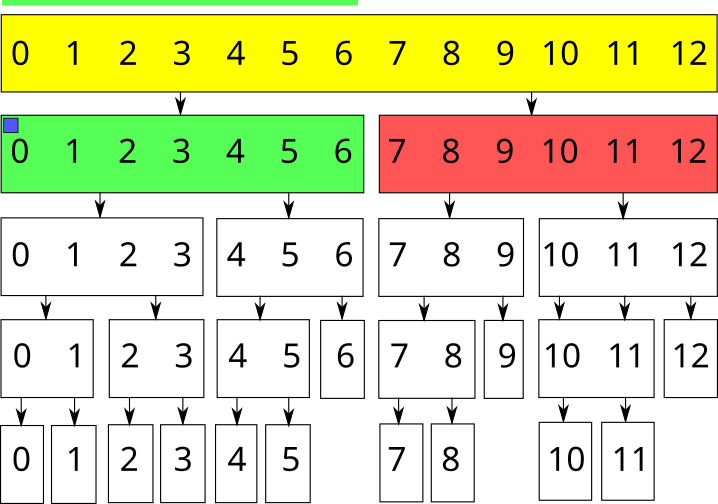
Например, отрезок \([1; 11]\) в массиве длиной \(13\) можно представить с помощью следующих вершин:

Дерево отрезков для поиска суммы

Одна из простейших функций, которую можно считать за \(O(\log N)\) с помощью дерева отрезков — сумма.

При построении дерева в каждой его вершине сохраним сумму на соответствующем отрезке (построение будет вестись рекурсивно, поэтому достаточно просто сложить суммы на двух дочерних отрезках). Затем каждый запрос суммы на отрезке будем разбивать на \(2 \log N\) отрезков, и находить сумму на каждом из них за \(O(1)\), используя предпросчитанные значения. Таким образом сложность запроса суммы равна \(O(\log N)\).

Кроме запросов суммы к дереву отрезков также могут поступать запросы на изменение отдельных элементов (модификацию). Заметим, что от изменения одного элемента значение суммы изменится в одной вершине на каждом уровне дерева отрезков (в которую входит этот элемент). Пересчитаем значения суммы (опять же, рекурсивно) только в этих вершинах. Таким образом сложность запроса модификации равна высоте дерева, или \(O(\log N)\).

Для реализации запроса суммы и запроса модификации обход дерева реализуется с помощью одного и того же алгоритма, основанного на DFS. Пусть границы нашего запроса \([L; R]\) (в случае запроса модификации \(L = R\)), а границы отрезка, соответствующего текущей вершине \([TL; TR]\). В зависимости от взаимного положения этих границ, существуют три варианта действий алгоритма:

• Текущий отрезок полностью входит в запрос (\(L \le TL; TR \le R\)). Если это запрос суммы, вернём предпросчитанную сумму на отрезке. Если это запрос модификации, изменим элемент и пересчитаем сумму. В дочерние вершины спускаться нет надобности.
• Текущий отрезок полностью не входит в запрос (\(TR < L\) или \(R < TL\)). Никаких действий выполнять не нужно, просто выйдем из функции. Если это запрос суммы, просто вернём \(0\).
• Текущий отрезок частично входит в запрос. Вызовем функцию рекурсивно для двух дочерних отрезков. Если это запрос суммы, вернём сумму двух полученных значений. Если это запрос модификации, пересчитаем значение суммы для текущего отрезка (так как оно могло измениться).

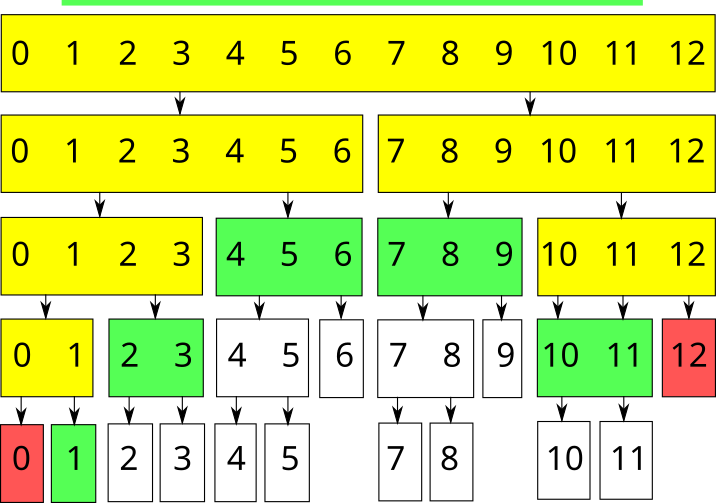
Обозначим эти варианты соответственно зелёным, красным и жёлтым цветом. Тогда запрос суммы на отрезке \([1; 11]\) массива длиной \(13\) будет обработан следующим образом:

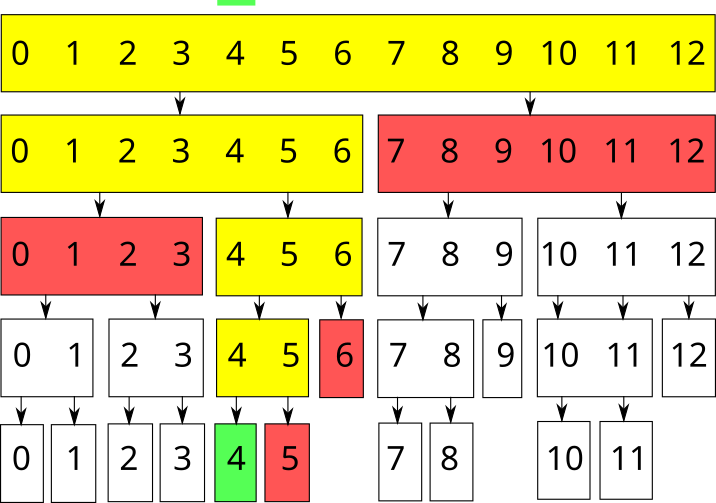
А запрос модификации \(4\)-го элемента:

Реализация дерева отрезков для поиска суммы

Полное бинарное дерево представляем, как и, например, кучу, с помощью массива и формул перехода \(l = 2v\) и \(r = 2v + 1\). Для предотвращения всех возможных переполнений размер дерева отрезков для массива из \(n\) элементов принимают равным \(4n\).

brestprog

Источник