Радиус дерева через диаметр

Остов графа. Примеры.

Для любого графа определяется понятие остовного дерева (остова) – суграф данного графа, являющийся деревом. Количество остовов дерева можно вычислить через измененную матрицу смежности: 1) изменяем у всех элементов знаки на противоположные; 2) главную диагональ заменяем на степени соответствующих вершин; 3) вычисляем алгебраические дополнения главной диагонали (у всех элементов они равны), значение которых и есть количество остовов.

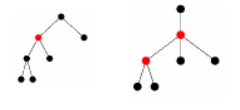
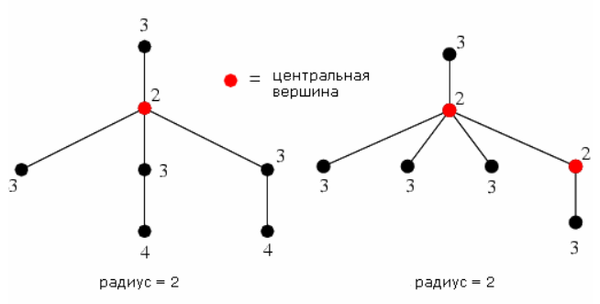
Центральные и бицентральные деревья. Радиус и диаметр дерева. Примеры.

Длина максимальной ветки дерева называется его высотой (h).

Расстояние от корня до вершины — уровень вершины (ребра).

Вершины одного уровня – ярус дерева.

Висячие вершины (ребра) имеют I уровень.

Вершина(-ы) максимального уровня называются центром (-ами) дерева.

Если в дереве 1 центр, то оно центрально, если 2 центра, то бицентрально.

Цепи, проходящие через центр(ы), называются диаметральными, а наибольшая из них – диаметр дерева.

Каждая вершина дерева имеет кортеж (последовательность натуральных чисел)- количество вершин соответствующей ветки.

Кортежи центров называются центральными.

Длина кортежа равна своему первому числу.

У изоморфных деревьев центральные кортежи совпадают.

Эйлеровы цепи и циклы. Эйлеровы графы. Теорема Эйлера. Примеры.

Граф, в котором есть замкнутая цепь (в орграфе – контур), называется графом с циклом. В графе может быть несколько циклов. Каждое ребро графа может принадлежать сразу нескольким циклам.

Количество циклов в графе называется цикломатическим числом.

Ясно, что цикломатическое число дерева =0.

Степень числа – количество инцидентных ему ребер. Валентность – степень с учетом двойного вхождения петли.

Обход графа – некоторое перечисление всех его вершин и (или) ребер.

В конечном связном графе всегда можно построить ориентированный цикл, проходящий через каждое ребро по одному разу в каждом направлении (обход ребер графа).

Простой цикл, содержащий все ребра графа ровно один раз, называется эйлеровым.

Граф, содержащий хотя бы один эйлеров цикл, называется эйлеровым графом.

На диаграмме эйлеров граф можно провести, не отрывая карандаша от бумаги и не проводя одно и то же ребро дважды.

Теорема Эйлера: конечный неориентированный граф эйлеров тогда и только тогда, когда

1. он связен;
2. он нетривиален (не состоит только из одной вершины);
3. каждая вершина имеет четную валентность;
4. множество ребер можно разбить на простые циклы.

1. в несвязном графе невозможно построить цикл, проходящий по всем ребрам,  граф должен быть связен;

2. тривиальный граф не имеет ребер,  нет возможности построить цикл;

3. при построении обхода графа будем задавать ребрам направления, тогда в любой вершине у каждого входа должен быть выход, иначе цикла не получится. Эйлеров граф может иметь кратные ребра, петли в нем не имеют смысла.

4. из 2. , что удаление одного цикла превращает граф в эйлеров граф (сохраняет четность валентности вершин) или в пустой граф, но никак не в дерево, т.е. в эйлеровом графе множество ребер можно разбить на простые циклы.

Простая открытая цепь, проходящая по всем ребрам графа, называется эйлеровой цепью.

Для наличия в графе эйлеровой цепи необходимо, чтобы граф был связен, и степени промежуточных вершин были четными. Вершины с нечетными степенями будут концами этой цепи. Для нахождения наименьшего количества эйлеровых цепей в графе достаточно количество вершин нечетной степени поделить пополам.

Для орграфа эйлеровость характеризуется равенством входов и выходов.

В любом графе число вершин нечетной степени четно.

Источник

Доказываем корректность поиска диаметра дерева

Однажды на зачете мне попалась следующая задача. Придумайте алгоритм, находящий две вершины дерева с максимальным расстоянием друг от друга, и докажите его корректность. В тот момент я в принципе не знала, что у деревьев есть диаметр, радиус и много прочих вещей. Уже после зачета друг просветил меня, рассказав, что это за алгоритм, но без доказательства. Именно вопросом о доказательстве долгое время была забита моя голова. После прочтения нескольких статей, стало понятно, что материал не уляжется, пока самостоятельно себе не объясню все практически на пальцах (может, и читателю придется по вкусу). Перейдем от демагогии к сути.

Диаметр дерева — это максимальное расстояние между двумя вершинами в дереве. Алгоритм поиска состоит в двух запусках BFS. Первый идет от произвольной вершины дерева, во время обхода насчитываются расстояния от текущей вершины до всех других. Затем из них выбирается самая удаленная. Из нее делается второй запуск BFS. Насчитываются новые расстояния. Максимальное среди них и будет диаметром.

Почему этот простой с виду алгоритм работает корректно?

Чтобы избежать подводных камней при доказательстве, сразу обговорим случай с деревом из одной вершины и из двух вершин. Если вершина одна, то ребер у нас нет, первый BFS сообщит, что стартовая вершина имеет максимальную глубину, второй — тоже. По сути это и есть так, алгоритм сработает верно. Если имеется две вершины, то первый обход придет во вторую вершину, а второй — в стартовую, что корректно для данного случая.

Сначала поймем, что искомое расстояние — расстояние между двумя листами. На самом деле, пусть вершина на конце найденного максимального путь не является листом. Одновременно мы не можем увеличить искомое расстояние по предположению. Тем не менее, это означает, что BFS не посетил вершины, «расположенные за» текущей, что противоречит корректности BFS. Получается, что обе найденные вершины будут листьями. Прекрасно.

Подвесим наше дерево за вершину v, из которой запускаем первый обход.

Рассмотрим отдельный случай, когда вершина v сама является листом. В случае, если она и есть первый конец диаметра, то очевидно, что первый BFS найдет второй конец, а второй вернется в стартовую вершину. Иначе диаметр не будет проходить через v и также будет «перегибаться», так как не может содержать более двух листьев.

Пусть мы нашли диаметр и две вершины, ему соответствующие. Найдем LCA этих вершин a и b, назовем эту вершину c. Очевидно, что D = d[a,c] + d[c,b]. Фактически диаметр это сумма двух наиболее глубоких поддеревьев некоторой вершины, если она принадлежит длиннейшему пути. Диаметр дерева — это максимальный диаметр среди всех поддеревьев. Первый обход в ширину даст нам максимальную по глубине вершину (так как мы подвесили за стартовую вершину). Обозначим вершину на конце найденного пути w. Докажем, что w будет принадлежать искомому длиннейшему пути. Пусть диаметр «перегибается» в вершине c(он будет «перегибаться», так как соединяет два листа, а дерево подвешено за вершину v, не являющуюся листом). Пускай вершина w принадлежит одному из поддеревьев вершины c. Тогда просто заменим некоторую часть пути (c, x), где x — один из концов, на (c, w). d[c,x] < d[c,w].Мы улучшили ответ. Значит, первоначальный путь не был диаметром. Если w является предком c, то w не является листом, поэтому этот случай отпадает. Если же w находится где-то в другом поддереве, то пусть e = LCA(c, w). d[w,e] — максимальная глубина поддерева e. Тогда так как e — предок c, то d[x, e] > d[x,c]. d[w,e] > d[y,e] > d[y,c]. Поэтому D0 = d[x,c] + d[y,c] < d[x, e] + d[w, e] = D. Значит, первоначально диаметр был найден неверно и вершина w принадлежит диаметру.

Примечание:
В данной части доказательства мы использовали свойство, что лист w имеет наибольшую глубину в любом поддереве данного дерева, которому принадлежит w. Докажем по индукции. База — один лист w. Очевидно, что утверждение верно. Пусть для некоторого поддерева это тоже верно, тогда поднимемся на уровень выше. Допустим, существует вершина, у которой глубина в текущем поддереве больше, чем у w. Назовем текущую вершину a, вершину с предполагаемой большей глубиной x, корень дерева v.
d[v,x] = d[v,a] + d[a,x];
d[v,w] = d[v,a] + d[a,w];
d[v,x] < d[v,w]в силу корректности работы BFS;
d[a,x] > d[a,w] по предположению;
В итоге получаем противоречие. Поэтому вершина w обладает наибольшей глубиной в любом поддереве.

Получаем, что вершина w принадлежит диаметру, а также является одним из его концов. Тогда очевидно, что остается лишь найти наиболее удаленную от w вершину, что и делает второй BFS.

Источник

Алгоритмы на деревьях

Пусть дан граф [math]G = \langle V, E \rangle [/math] . Тогда диаметром [math]d[/math] называется [math]\max\limits_ dist(v, u)[/math] , где [math]dist[/math] — кратчайшее расстояние между вершинами.

Алгоритм

• Возьмём любую вершину [math] v \in V [/math] и найдём расстояния до всех других вершин. [math]d[i] = dist(v, i)[/math]

• Возьмём вершину [math] u \in V [/math] такую, что [math]d[u] \geqslant d[t][/math] для любого [math]t[/math] . Снова найдём расстояние от [math]u[/math] до всех остальных вершин. Самое большое расстояние — диаметр дерева.

Расстояние до остальных вершин будем искать алгоритмом [math]BFS[/math] .

Реализация

//граф g представлен списком смежности int diameterTree(list> g): v = u = w = 0 d = bfs(g, v) for i = 0, i < n, i++ if d[i] > d[u] u = i d = bfs(g, u) for i = 0, i < n, i++ if d[i] > d[w] w = i return d[w]

Обоснование корректности

Будем пользоваться свойством, что в любом дереве больше одного листа. Исключительный случай — дерево из одной вершины, но алгоритм сработает верно и в этом случае.

После запуска алгоритма получим дерево [math]BFS[/math] .

В дереве [math]BFS[/math] не существует ребер между вершинами из разных поддеревьев некоторого их общего предка.

Предположим, существует ребро [math]u, v[/math] между соседними поддеревьями:

Мы свели задачу к нахождению вершины [math]w[/math] , такой что сумма глубин поддеревьев максимальна.

Докажем, что одно из искомых поддеревьев содержит самый глубокий лист. Пусть нет, тогда, взяв расстояние от [math]w[/math] до глубочайшего листа, мы можем улучшить ответ.

Таким образом мы доказали, что нам нужно взять вершину [math]u[/math] с наибольшей глубиной после первого [math]BFS[/math] , очевидно, что ей в пару надо сопоставить вершину [math]w[/math] , такую что [math]dist(u, w)[/math] максимально. Вершину [math]w[/math] можно найти запуском [math]BFS[/math] из [math]u[/math] .

Оценка времени работы

Все операции кроме [math]BFS[/math] — [math]O(1)[/math] . [math]BFS[/math] работает за линейное время, запускаем мы его два раза. Получаем [math]O(|V| + |E|)[/math] .

Центр дерева

Определения

Определение:

Эксцентриситет вершины [math]e(v)[/math] (англ. eccentricity of a vertex) — [math]\max\limits_ dist(v, u)[/math] , где [math]V[/math] — множество вершин связного графа [math]G[/math] .

Определение:

Радиус [math]r(G)[/math] (англ. radius) — наименьший из эксцентриситетов вершин графа [math]G[/math] .

Определение:

Центральная вершина (англ. central vertex) — вершина графа [math]G[/math] , такая что [math]e(v) = r(G)[/math]

Определение:

Центр графа [math]G[/math] (англ. center of a graph) — множество всех центральных вершин графа [math]G[/math] .

Алгоритм

Наивный алгоритм

Найдём центр графа исходя из его определения.

• Построим матрицу [math]A_[/math] ( [math]n[/math] — мощность множества [math]V[/math] ), где [math]a_ = d_[/math] , то есть матрицу кратчайших путей. Для её построения можно воспользоваться алгоритмом Флойда-Уоршелла или Дейкстры.
• Подсчитаем максимум в каждой строчке матрицы [math]A[/math] . Таким образом, получим массив длины [math]n[/math] .
• Найдём наименьший элемент в этом массиве. Эта вершина и есть центр графа. В том случае, когда вершин несколько, все они являются центрами.

Асимптотика зависит от используемого способа подсчета кратчайших путей. При Флойде это будет [math]O(V^3)[/math] , а при Дейкстре — максимум из асимптотики конкретной реализации Дейкстры и [math]O(V^2)[/math] , за которую мы находим максимумы в матрице.

Алгоритм для дерева за O(n)

Собственно, алгоритм нахождения центра описан в доказательстве теоремы.

• Пройдёмся по дереву обходом в глубину и пометим все висячие вершины числом [math]0[/math] .
• Обрежем помеченные вершины.
• Образовавшиеся листья пометим числом [math]1[/math] и тоже обрежем.
• Будем повторять, пока на текущей глубине не окажется не более двух листьев, и при этом в дереве будет тоже не более двух листьев.

Оставшиеся листья являются центром дерева.

Для того, чтобы алгоритм работал за [math]O(n)[/math] , нужно обрабатывать листья по одному, поддерживая в очереди два последовательных по глубине слоя.

См. также

Источники информации

Источник