Разновидность деревьев базы данных

Обзор паттернов хранения деревьев в реляционных БД

Всем привет! Меня зовут Пантелеев Александр и я бэкенд-разработчик в компании Bimeister.

Постараюсь описать исчерпывающе, кратко и понятно суть основных паттернов хранения деревьев в реляционных базах данных. Надеюсь, что статья будет полезна тем, кто до сего момента не сталкивался с такими паттернами, и станет отправной точкой в их понимании.

В этой статье не будет терминов реляционной алгебры или базы данных: таких как атрибут, домен и т. д. Также не будет привязки к какой-либо СУБД, какому-либо SQL или пользовательскому коду.

Всего существует 4 общепринятых паттерна хранения деревьев:

Кратко рассмотрим каждый из них.

Adjacency List

Описание

Это самый простой и интуитивный вариант хранения. Каждому элементу сопоставляется его свойство — его родительский элемент. Если родительский элемент не задан, то он считается корневым элементом.
Когда связь сопоставления элемента и родительского элемента хранится отдельно от элемента, Adjacency List можно рассматривать как частный случай Closure Table со связями 1 уровня.

Преимущества

Лёгкость реализации, а также простота вставки, удаления и перемещения элементов в дереве.

Недостатки

Можно получить только непосредственные дочерние элементы. Чтобы получить все дочерние элементы, необходимо выполнить рекурсивный запрос либо производить множественные запросы.

Примеры

Родительский элемент

Чтобы получить все его дочерние элементы, нам необходимо выбрать элементы, удовлетворяющие условию:

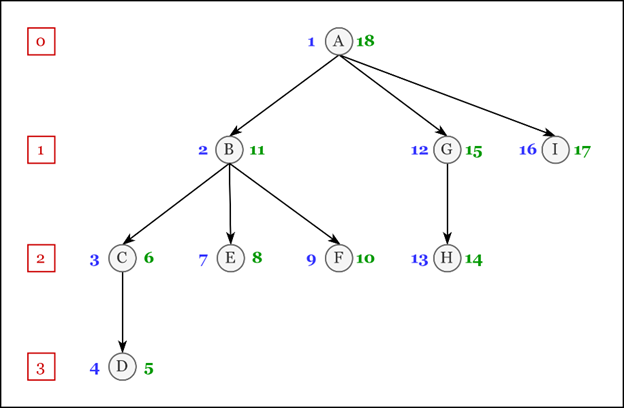
Nested Sets

Описание

Каждому элементу сопоставляются свойства: левый и правый индекс, на основе которых будет производиться выборка дочерних элементов. Также, но необязательно, элемент может дополняться свойством уровень для указания желаемого уровня вложенности выбираемого элемента относительно корня или родительского элемента.

Запрос получения дочерних элементов строится на том факте, что для любого дочернего элемента выполняются условия:

• левый индекс больше левого индекса родительского элемента;
• правый индекс меньше правого индекса родительского элемента.

При создании и обновлении дерева левые и правые индексы элементов дерева, при его обходе в глубину, заполняются по определённым правилам.

Преимущества

Возможность получения дочерних элементов любых уровней вложенности с помощью простого одиночного запроса.

Недостатки

При использовании целочисленных типов для левого и правого индекса и уровня необходимо пересчитывать индексы всех связанных элементов в следующих случаях:

• при вставке элементов;
• при удалении элементов;
• при изменении родительского элемента.

Пример

Левый индекс

Правый индекс

Рассмотрим элемент «B». Его значения свойств:

Чтобы получить все его дочерние элементы, нам необходимо выбрать элементы, удовлетворяющие условию:

левый индекс больше 2 И правый индекс меньше 11

Чтобы получить его непосредственные дочерние элементы, нам необходимо добавить к условию ограничение на уровень:

левый индекс больше 2 И правый индекс меньше 11 И уровень = 1

Чтобы получить дочерние элементы вместе с родительским элементом, нам необходимо ослабить условия индексов:

левый индекс больше или равен 2 И правый индекс меньше или равен 11

Closure Table

Описание

Суть этого паттерна заключается в том, что мы сопоставляем каждому элементу множество связей со всеми его дочерними элементами или сопоставляем каждому элементу множество связей со всеми его родительскими элементами. Также, но необязательно, связь может содержать свойство Уровень. Уровень задаёт расстояние между элементами в дереве.

Если в запросе получения дочерних или родительских элементов по элементу необходимо получать в результате сам элемент, то нужно добавлять связь элемента самого на себя — то есть со значением уровня связи 0.

Преимущества

Возможность получения дочерних элементов любых уровней вложенности с помощью простого одиночного запроса.

Возможность получения родительских элементов любых уровней с их иерархией относительно дочернего элемента с помощью простого одиночного запроса.

Недостатки

При вставке и удалении элементов из дерева, а также при перемещении элементов в дереве необходимо пересчитывать все связи, в которых этот элемент участвует.

Источник

Деревья

Дерево — это нелинейная иерархическая структура данных. Она состоит из узлов и ребер, которые соединяют узлы.

Зачем нужны деревья

Другие структуры данных, например, массивы, списки, стеки и очереди, линейные. Это значит, что данные в них хранятся последовательно. Когда мы выполняем любую операцию в линейной структуре данных, временная сложность растет с увеличением размера данных. В современном мире это не очень круто.

Разные древовидные структуры позволяют быстрее и легче получать доступ к данным, поскольку дерево — структура нелинейная.

Части дерева

• Узел — это объект, в котором есть ключ или значение и указатели на дочерние узлы.
  Узлы, у которых нет дочерних узлов, называют листами или терминальными узлами.
  Узлы, у которых есть хотя бы один дочерний узел, называются внутренними.
• Ребро связывает два узла.
• Корень — это самый верхний узел дерева. Его ещё иногда называют корневым узлом.

Другие понятия

• Высота узла — это максимальная длина пути от этого узла к самому нижнему узлу (листу).
• Глубина вложенности узла — длина пути от корня до этого узла.
• Высота дерева — это высота корневого узла или глубина самого глубокого узла.
• Степень узла — это общее количество ребер, которые соединены с этим узлом.

• Лес — множество непересекающихся деревьев. Например, если «срезать» корень, получится лес.

Виды деревьев

Обход дерева

Чтобы выполнить какую-либо операцию с деревом, нужно добраться до определенного узла. Для этого и существуют алгоритмы обхода дерева. Они помогают «дойти» до необходимого узла.

Где используются

• Деревья двоичного поиска помогают быстро проверить наличие элемента в наборе.
• Куча — это тоже своеобразное дерево. Кучи используют в алгоритме сортировки кучей.
• Префиксные деревья используются в маршрутизаторах, они хранят информацию о маршруте.
• Большинство популярных баз данных основаны на B-деревья и T-деревья.
• Компиляторы используют абстрактное синтаксическое дерево, чтобы находить синтаксические ошибки в ваших программах.

СodeСhick.io — простой и эффективный способ изучения программирования.

2023 © ООО «Алгоритмы и практика»

Источник