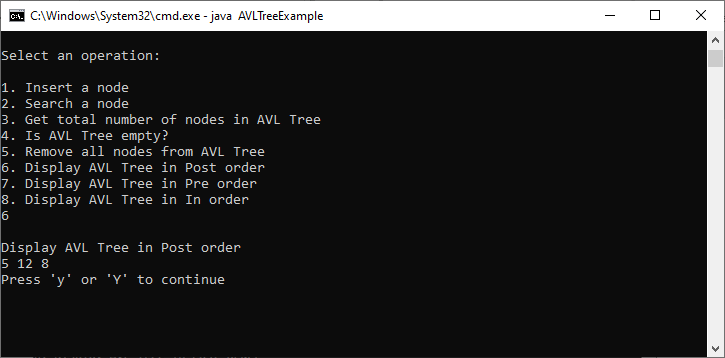
Implementing an AVL tree in JAVA
I need to implement the add and remove functions. Here is what I have so far, both should run in O(log(n)) time. Both should return the root of the whole tree:
/* Adds a new Node into the tree. * @param key the key of the new node * @param data the data of the new node */ public void add(Object key,Object data) < if (isEmpty())< this.root = new AVLNode(key,data,comp); >else < root = this.root.add(key,data); >> /** * Removes a node n from the tree where * n.key is equal (by ) to the given key. * * @param key the key */ public void remove(Object key) < if (isEmpty())< return; >else root = this.root.remove(key); > I need help on making the add and remove functions. Is there any guide to describe how the add and remove operations work? A library to copy or something where I can figure out how/why AVL Trees work?
4 Answers 4
You can try my AVL Tree which is linked here. Let me know if you have any additional questions.
Source in case the link goes down
package com.jwetherell.algorithms.data_structures; import java.util.ArrayList; import java.util.List; /** * An AVL tree is a self-balancing binary search tree, and it was the first such * data structure to be invented. In an AVL tree, the heights of the two child * subtrees of any node differ by at most one. AVL trees are often compared with * red-black trees because they support the same set of operations and because * red-black trees also take O(log n) time for the basic operations. Because AVL * trees are more rigidly balanced, they are faster than red-black trees for * lookup intensive applications. However, red-black trees are faster for * insertion and removal. * * http://en.wikipedia.org/wiki/AVL_tree * * @author Justin Wetherell */ public class AVLTree> extends BinarySearchTree implements BinarySearchTree.INodeCreator < private enum Balance < LEFT_LEFT, LEFT_RIGHT, RIGHT_LEFT, RIGHT_RIGHT >; /** * Default constructor. */ public AVLTree() < this.creator = this; >/** * Constructor with external Node creator. */ public AVLTree(INodeCreator creator) < super(creator); >/** * */ @Override protected Node addValue(T id) < NodenodeToReturn = super.addValue(id); AVLNode nodeAdded = (AVLNode) nodeToReturn; while (nodeAdded != null) < nodeAdded.updateHeight(); balanceAfterInsert(nodeAdded); nodeAdded = (AVLNode) nodeAdded.parent; > return nodeToReturn; > /** * Balance the tree according to the AVL post-insert algorithm. * * @param node * Root of tree to balance. */ private void balanceAfterInsert(AVLNode node) < int balanceFactor = node.getBalanceFactor(); if (balanceFactor >1 || balanceFactor < -1) < AVLNodeparent = null; AVLNode child = null; Balance balance = null; if (balanceFactor < 0) < parent = (AVLNode) node.lesser; balanceFactor = parent.getBalanceFactor(); if (balanceFactor < 0) < child = (AVLNode) parent.lesser; balance = Balance.LEFT_LEFT; > else < child = (AVLNode) parent.greater; balance = Balance.LEFT_RIGHT; > > else < parent = (AVLNode) node.greater; balanceFactor = parent.getBalanceFactor(); if (balanceFactor < 0) < child = (AVLNode) parent.lesser; balance = Balance.RIGHT_LEFT; > else < child = (AVLNode) parent.greater; balance = Balance.RIGHT_RIGHT; > > if (balance == Balance.LEFT_RIGHT) < // Left-Right (Left rotation, right rotation) rotateLeft(parent); rotateRight(node); >else if (balance == Balance.RIGHT_LEFT) < // Right-Left (Right rotation, left rotation) rotateRight(parent); rotateLeft(node); >else if (balance == Balance.LEFT_LEFT) < // Left-Left (Right rotation) rotateRight(node); >else < // Right-Right (Left rotation) rotateLeft(node); >node.updateHeight(); // New child node child.updateHeight(); // New child node parent.updateHeight(); // New Parent node > > /** * */ @Override protected Node removeValue(T value) < // Find node to remove NodenodeToRemoved = this.getNode(value); if (nodeToRemoved != null) < // Find the replacement node NodereplacementNode = this.getReplacementNode(nodeToRemoved); // Find the parent of the replacement node to re-factor the // height/balance of the tree AVLNode nodeToRefactor = null; if (replacementNode != null) nodeToRefactor = (AVLNode) replacementNode.parent; if (nodeToRefactor == null) nodeToRefactor = (AVLNode) nodeToRemoved.parent; if (nodeToRefactor != null && nodeToRefactor.equals(nodeToRemoved)) nodeToRefactor = (AVLNode) replacementNode; // Replace the node replaceNodeWithNode(nodeToRemoved, replacementNode); // Re-balance the tree all the way up the tree if (nodeToRefactor != null) < while (nodeToRefactor != null) < nodeToRefactor.updateHeight(); balanceAfterDelete(nodeToRefactor); nodeToRefactor = (AVLNode) nodeToRefactor.parent; > > > return nodeToRemoved; > /** * Balance the tree according to the AVL post-delete algorithm. * * @param node * Root of tree to balance. */ private void balanceAfterDelete(AVLNode node) < int balanceFactor = node.getBalanceFactor(); if (balanceFactor == -2 || balanceFactor == 2) < if (balanceFactor == -2) < AVLNodell = (AVLNode) node.lesser.lesser; int lesser = (ll != null) ? ll.height : 0; AVLNode lr = (AVLNode) node.lesser.greater; int greater = (lr != null) ? lr.height : 0; if (lesser >= greater) < rotateRight(node); node.updateHeight(); if (node.parent != null) ((AVLNode) node.parent).updateHeight(); > else < rotateLeft(node.lesser); rotateRight(node); AVLNodep = (AVLNode) node.parent; if (p.lesser != null) ((AVLNode) p.lesser).updateHeight(); if (p.greater != null) ((AVLNode) p.greater).updateHeight(); p.updateHeight(); > > else if (balanceFactor == 2) < AVLNoderr = (AVLNode) node.greater.greater; int greater = (rr != null) ? rr.height : 0; AVLNode rl = (AVLNode) node.greater.lesser; int lesser = (rl != null) ? rl.height : 0; if (greater >= lesser) < rotateLeft(node); node.updateHeight(); if (node.parent != null) ((AVLNode) node.parent).updateHeight(); > else < rotateRight(node.greater); rotateLeft(node); AVLNodep = (AVLNode) node.parent; if (p.lesser != null) ((AVLNode) p.lesser).updateHeight(); if (p.greater != null) ((AVLNode) p.greater).updateHeight(); p.updateHeight(); > > > > /** * */ @Override protected boolean validateNode(Node node) < boolean bst = super.validateNode(node); if (!bst) return false; AVLNodeavlNode = (AVLNode) node; int balanceFactor = avlNode.getBalanceFactor(); if (balanceFactor > 1 || balanceFactor < -1) < return false; >if (avlNode.isLeaf()) < if (avlNode.height != 1) return false; >else < AVLNodeavlNodeLesser = (AVLNode) avlNode.lesser; int lesserHeight = 1; if (avlNodeLesser != null) lesserHeight = avlNodeLesser.height; AVLNode avlNodeGreater = (AVLNode) avlNode.greater; int greaterHeight = 1; if (avlNodeGreater != null) greaterHeight = avlNodeGreater.height; if (avlNode.height == (lesserHeight + 1) || avlNode.height == (greaterHeight + 1)) < return true; >else < return false; >> return true; > /** * */ @Override public String toString() < return AVLTreePrinter.getString(this); >/** * */ @Override public Node createNewNode(Node parent, T id) < return (new AVLNode(parent, id)); > protected static class AVLNode> extends Node < protected int height = 1; /** * Constructor for an AVL node * * @param parent * Parent of the node in the tree, can be NULL. * @param value * Value of the node in the tree. */ protected AVLNode(Nodeparent, T value) < super(parent, value); >/** * Determines is this node is a leaf (has no children). * * @return True if this node is a leaf. */ protected boolean isLeaf() < return ((lesser == null) && (greater == null)); >/** * Updates the height of this node based on it's children. */ protected void updateHeight() < int lesserHeight = 0; int greaterHeight = 0; if (lesser != null) < AVLNodelesserAVLNode = (AVLNode) lesser; lesserHeight = lesserAVLNode.height; > if (greater != null) < AVLNodegreaterAVLNode = (AVLNode) greater; greaterHeight = greaterAVLNode.height; > if (lesserHeight > greaterHeight) < height = lesserHeight + 1; >else < height = greaterHeight + 1; >> /** * Get the balance factor for this node. * * @return An integer representing the balance factor for this node. It * will be negative if the lesser branch is longer than the * greater branch. */ protected int getBalanceFactor() < int lesserHeight = 0; int greaterHeight = 0; if (lesser != null) < AVLNodelesserAVLNode = (AVLNode) lesser; lesserHeight = lesserAVLNode.height; > if (greater != null) < AVLNodegreaterAVLNode = (AVLNode) greater; greaterHeight = greaterAVLNode.height; > return greaterHeight - lesserHeight; > /** * */ @Override public String toString() < return "value=" + id + " height=" + height + " parent=" + ((parent != null) ? parent.id : "NULL") + " lesser=" + ((lesser != null) ? lesser.id : "NULL") + " greater=" + ((greater != null) ? greater.id : "NULL"); >> protected static class AVLTreePrinter < public static > String getString(AVLTree tree) < if (tree.root == null) return "Tree has no nodes."; return getString((AVLNode) tree.root, "", true); > public static > String getString(AVLNode node) < if (node == null) return "Sub-tree has no nodes."; return getString(node, "", true); >private static > String getString(AVLNode node, String prefix, boolean isTail) < StringBuilder builder = new StringBuilder(); builder.append(prefix + (isTail ? "└── " : "├── ") + "(" + node.height + ") " + node.id + "\n"); List children = null; if (node.lesser != null || node.greater != null) < children = new ArrayList(2); if (node.lesser != null) children.add(node.lesser); if (node.greater != null) children.add(node.greater); > if (children != null) < for (int i = 0; i < children.size() - 1; i++) < builder.append(getString((AVLNode) children.get(i), prefix + (isTail ? " " : "│ "), false)); > if (children.size() >= 1) < builder.append(getString((AVLNode) children.get(children.size() - 1), prefix + (isTail ? " " : "│ "), true)); > > return builder.toString(); > > > Источник
AVL Tree program in Java
Just like the Red-Black Tree, the AVL tree is another self-balancing BST(Binary Search Tree) in Java. In the AVL tree, the difference between heights of the right and left subtree doesn’t exceed one for all nodes. It takes O(h) time to perform the search, max, min, insert, and delete BST operations. Here, the h is the height of the Binary Search Tree.
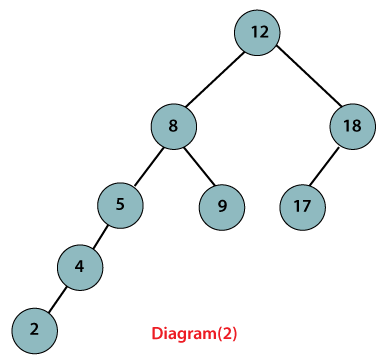
Let’s take an example of an AVL tree and a tree that is not AVL to understand the difference between both of them,
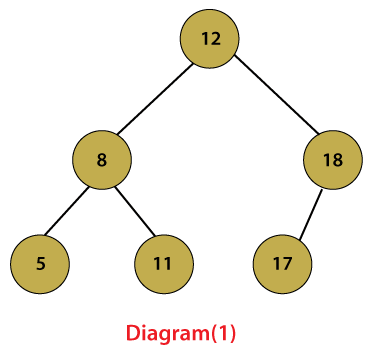
Diagram(1) is an example of the AVL tree because the difference between the heights of the left and right sub-tree is 1. Diagram (2) is not an AVL tree because the difference between the heights of the left and right subtree is not 1.
Let’s understand the algorithm of inserting a node in the AVL Tree:
Suppose the newNode is the newly inserted node in the AVL Tree.
- We will insert the newNode in the AVL Tree by performing the standard BST insert operation.
- We will go through the AVL Tree from the newNode and check for that node that is unbalanced. Suppose unBalNode is the first unbalanced node, childNode is the child node of the unBalNode that comes on the path from newNode to unBalNode, and newNode is the grandchild of the unBalNode that comes from the path from newNode to unBalNode.
- After that, we perform the appropriate rotations on the subtree rooted with unBalNode to re-balance the AVL Tree. These are the following four cases which we need to be handled.
- When childNode is the left child of the unBalNode and newNode is the left child of the childNode. This case is known as Left Left Case.
- When the childNode is the left child of the unBalNode, and the newNode is the right child of the childNode. This case is known as Left Right Case.
- When the childNode is the right child of the unBalNode, and the newNode is the right child of the childNode. This case is known as Right Right Case.
- When the childNode is the right child of the unBalNode, and the newNode is the left child of the childNode. This case is known as Right Left Case.
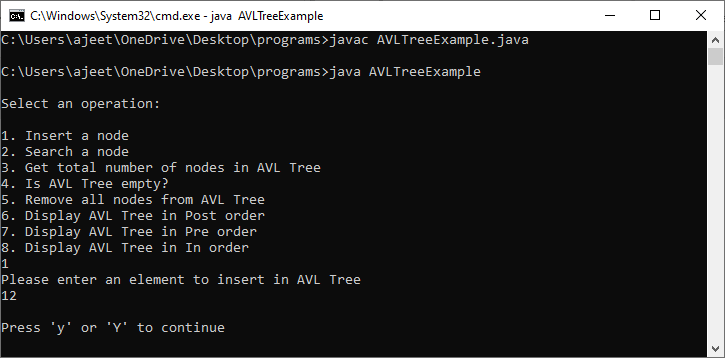
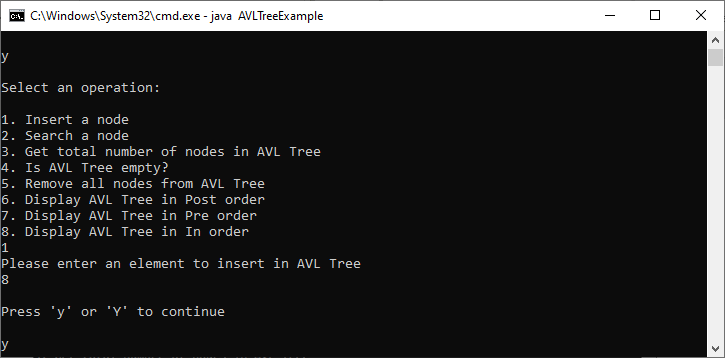
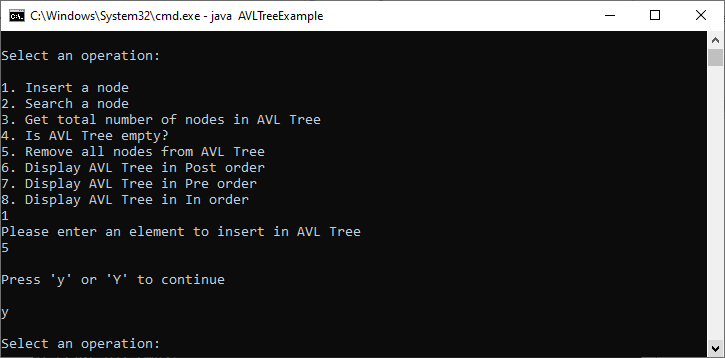
AVLTreeExample.java
For Videos Join Our Youtube Channel: Join Now
Feedback
Источник
Реализация avl дерева java
In the following sections, you will find the advantages and disadvantages of the AVL tree compared to similar data structures.
AVL Tree vs. Red Black Tree
- Searching in the AVL tree is usually faster than in the red-black tree because the AVL tree is better balanced.
- Insertions and deletions, on the other hand, are faster in a red-black tree because it rebalances less frequently.
- AVL trees need an extra byte per node for storing their height. Red-black trees need only one bit per node for the color information. In Java practice, this makes no difference as at least one byte is occupied for the bit anyway.
AVL Tree vs. Binary Search Tree
An AVL tree is a binary search tree that re-establishes the AVL invariant by rotation after each insert and delete operation.
A binary search tree does not necessarily have to be balanced. Likewise, we can achieve balancing by other than the AVL tree algorithm.
Therefore, every AVL tree is a binary search tree. But not every binary search tree is an AVL tree.
Conclusion
In this tutorial, you learned what an AVL tree is and how to rebalance it after insert or delete operations by single or double rotation. You also learned how to implement an AVL tree in Java.
The next part will be about another concrete type of binary search tree: the red-black tree. Would you like to receive an email when the article is published? Then click here to join the HappyCoders newsletter.
If you liked the article, feel free to share it using one of the share buttons at the end or drop me a comment.
Источник