18. Понятие рекурсивных структур данных. Деревья, их признаки и представления
Рекурсия — процесс, протекание которого связано с обращением к самому себе (к этому же процессу).
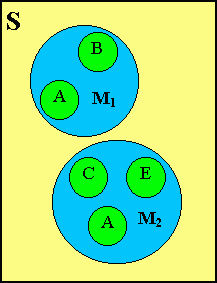
Пример рекурсивной структуры данных — структура данных, элементы которой являются такими же структурами данных (рис. 4.1).
Деревья входят в состав рекурсивных структур данных.
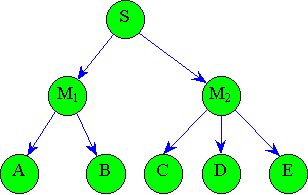
Дерево – нелинейная связанная структура данных (рис. 4.2).
Дерево характеризуется следующими признаками:
— дерево имеет 1 элемент, на которого нет ссылок от других элементов. Этот элемент называется корнем дерева;
— в дереве можно обратиться к любому элементу путем прохождения конечного числа ссылок (указателей);
— каждый элемент дерева связан только с одним предыдущим элементом. Любой узел дерева может быть промежуточным либо терминальным (листом). На рис. 4.2 промежуточными являются элементы М1, М2, листьями — А, В, С, В, Е. Характерной особенностью терминального узла является отсутствие ветвей.
Высота — это количество уровней дерева. У дерева на рис. 4.2 высота равна двум.
Количество ветвей, растущих из узла дерева, называется степенью исхода узла (на рис. 4.2 для М1 степень исхода 2, для М2 — З).
Деревья могут классифицироваться по степени исхода :
1) если максимальная степень исхода равна m то это – m-арное дерево;
2) если степень исхода равна либо 0, либо m то это — полное m-арное дерево;
З) если максимальная степень исхода равна 2, то это — бинарное дерево;
4) если степень исхода равна либо 0, либо 2, то это — полное бинарное дерево.
Для описание связей между узлами дерева применяют также следующую терминологию: М1 — “отец” для элементов А и В. А и В — “сыновья” узла М1.
Представление деревьев
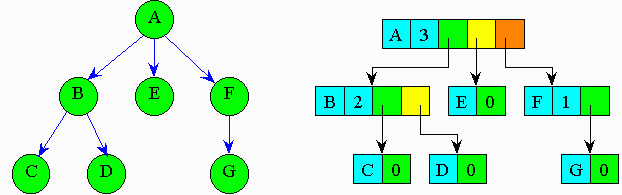
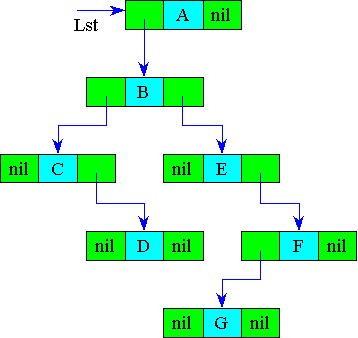
Наиболее удобно деревья представлять в памяти ЭВМ в виде связанных списков. Элемент списка должен содержа информационные поля, в которых содержится значение узла и степень исхода, а также — поля число которых равно степени исхода (рис4.З). То есть, любой указатель элемента ориентирует данный элемент с сыновьями этого узла.
Представление дерева в виде нелинейного списка
19. Алгоритм сведения m-арного дерева к бинарному; основные операции над деревьями; виды обхода
Бинарные деревья являются наиболее используемой разновидностью деревьев.
Согласно представлению деревьев в памяти ЭВМ каждый элемент будет записью, содержащей 4 поля. Значения этих полей будут соответственно ключ записи, ссылка на элемент влево-вниз, на элемент вправо-вниз и на текст записи.
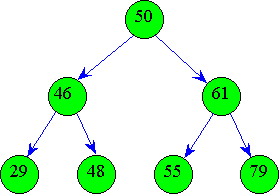
При построении необходимо помнить, что левый сын имеет ключ меньший, чем у отца, а значение ключа правого сына больше значения ключа отца. Например, построим бинарное дерево из следующих элементов: 50, 46, 61, 48, 29, 55, 79. Оно имеет следующий вид:
Получили упорядоченное бинарное дерево с одинаковым числом уровней в левом и правом поддеревьях. Это — идеально сбалансированное дерево, то есть дерево, в котором левое и правое поддеревья имеют уровни, отличающиеся не более чем на единицу.
Для создания бинарного дерева надо создавать в памяти элементы типа (рис. 4.5):
Операция V= MakeTree(Key, Rec) — создает элемент (узел дерева) с двумя указателями и двумя полями (ключевым и информационным).
Сведение m-арного дерева к бинарному
1.В любом узле дерева отсекаются все ветви, кроме крайней левой, соответствующей старшим сыновьям.
2.Соединяется горизонтальными линиями все сыновья одного родителя;
З. Старшим сыном в любом узле полученной структуры будет узел, находящийся под данным узлом (если он есть).
Последовательность действий алгоритма приведена на рис. 4.6.
Реализация полученного бинарного дерева с помощью нелинейного двусвязного списка
Основные операции с деревьями
Для выполнения обхода дерева необходимо выполнить три процедуры:
Обход дерева – это последовательная обработка информации в узлах дерева. В зависимости от того, в какой последовательности выполняются эти три процедуры, различают три вида обхода.
1 .Обход сверху вниз. Процедуры выполняются в последовательности 1-2-3.
2.Обход слева направо. Процедуры выполняются в последовательности 2-1-3.
3.Обход снизу вверх. Процедуры выполняются в последовательности 2-3-1.
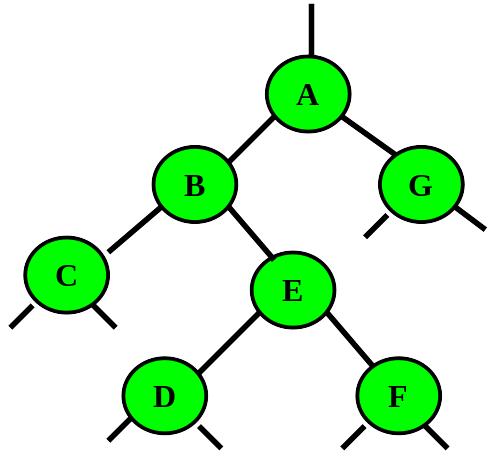
A-B-C-E-D-F-G – сверху вниз
C—B—D—E—F—A—G – слева направо
C—D—F—E—B—G—A – снизу вверх
В зависимости от того, какой по счету заход в узел приводит к обработке узла, получается реализация одного из трех видов обхода. Если обработка идет после первого захода в узел, то сверху вниз, если после второго, то слева направо, если после третьего, то снизу вверх
Операция исключения поддерева. Необходимо указать узел, к которому подсоединяется исключаемое поддерево и индекс этого поддерева. Исключение поддерева состоит в том, что разрывается связь с исключаемым поддеревом, т. е. указатель элемента устанавливается в nil, а степень исхода данного узла уменьшается на единицу.
Вставка поддерева — операция, обратная исключению. Надо знать индекс включаемого поддерева, узел, к которому подвешивается дерево, установить указатель этого узла на корень поддерева, а степень исхода данного узла увеличивается на единицу. При этом в общем случае необходимо произвести перенумерацию сыновей узла, к которому подвешивается поддерево.
Источник