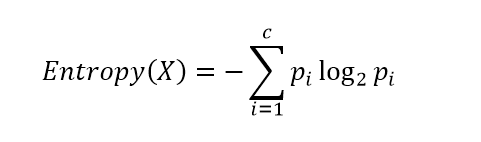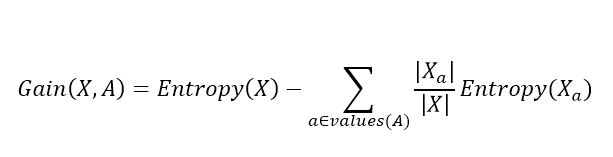Решение задач используя дерево решений

Использование деревьев решений в задачах прогнозной аналитики

В последние десятилетия одними из самых популярных методов решения задач прогнозной аналитики являются методы построения деревьев решений. Эти методы универсальны, используют эффективную процедуру вычислений, позволяют найти достаточно качественное решение задачи. Именно об этих методах я расскажу в данной статье.

Дерево решений

Дерево решений – структура данных, в процессе обхода которой в каждом узле в зависимости от проверяемого условия принимается определенное решение – перемещение по той или иной ветке дерева от корня к «листьевым» (конечным) вершинам. В «листьевой» вершине дерева содержится искомое значение интересующего атрибута. Деревья решений могут оценивать значения категориальных атрибутов (конечное число дискретных значений), а также количественных. В первом случае говорят о задаче классификации – отнесении объекта к одному из «классов», определяемых атрибутом (например, Да/Нет, Хорошо/Удовлетворительно/Плохо и т.д.). Во втором случае говорят о задаче регрессии, то есть об оценке количественной величины.

Мы рассмотрим алгоритм, позволяющий построить такое дерево решений для оценивания и предсказания значений интересующего нас категориального атрибута анализируемого набора данных на основе значений других атрибутов (задача классификации).

Вообще способов построить дерево может быть бесконечно много – атрибуты можно рассматривать в разном порядке, проверять в узлах дерева различные условия, останавливать процесс, используя разные критерии. Но нас интересуют только деревья, которые наиболее точно оценивают значение атрибута, с минимальной ошибкой, а также позволяют выявлять зависимость между атрибутами и успешно выполнять прогнозирование значений атрибутов на новых данных. К сожалению, не существует хороших алгоритмов, позволяющих гарантированно найти такое «оптимальное» дерево (за приемлемое время). Однако существуют достаточно хорошие алгоритмы, которые пытаются построить «почти оптимальное» дерево, выполняя на каждой итерации определенный «локальный» критерий оптимальности в надежде, что получившееся дерево тоже в целом будет «оптимальным». Такие алгоритмы называются «жадными». Именно такой алгоритм мы и рассмотрим.

Алгоритм построения дерева решений

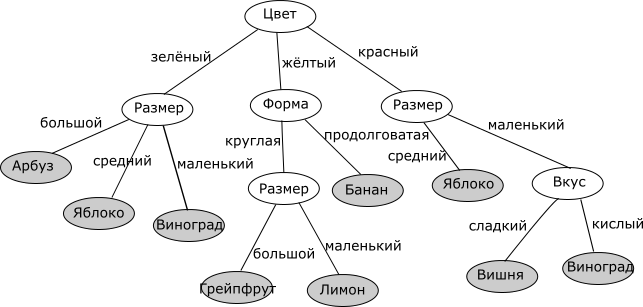
Принцип построения дерева следующий. Дерево строится «сверху вниз» от корня. Начинается процесс с определения, какой атрибут следует выбрать для проверки в корне дерева. Для этого каждый атрибут исследуется на предмет, как хорошо он в одиночку классифицирует набор данных (разделяет на классы по целевому атрибуту). Когда атрибут выбран, для каждого его значения создается ветка дерева, набор данных разделяется в соответствии со значением к каждой ветке, процесс повторяется рекурсивно для каждой ветки. Также следует проверять критерий остановки.

Главный вопрос – как выбирать атрибуты. В соответствии с идеей подхода, когда в концевых узлах дерева (листьях) будет искомый нами класс целевого атрибута, необходимо, чтобы при разбиении набора данных в каждом узле получавшиеся наборы данных были все более однородны в плане значений классов (например, большинство объектов в наборе принадлежало бы к классу Арбуз). И необходимо определить количественный критерий, чтобы оценить однородность разбиения.

Энтропия

Рассмотрим набор вероятностей pi, описывающий вероятность соответствия строки данных в нашем наборе (обозначим его X) классу i. Вычислим следующую величину:

Данная функция представляет собой так называемую энтропию. Энтропия возникла в теории информации и описывает количество информации (в битах), которое необходимо, чтобы закодировать сообщение о принадлежности случайно выбранного объекта (строки) из нашего набора X к одному из классов и передать его получателю. Если класс только один, получателю ничего не нужно передавать, энтропия равна 0 (принимается, что 0log20 = 0). Если все классы равновероятны, то потребуется log2c бит (c – общее количество классов) – максимум функции энтропии.

Далее, для выбора атрибута, для каждого атрибута A вычисляется так называемый прирост информации:

Где values(A) – все принимаемые значения атрибута A, Xa – подмножество набора данных, где A = a, |X| – количество элементов во множестве. Данная величина описывает ожидаемое уменьшение энтропии после разбиения набора данных по выбранному атрибуту. Второе слагаемое – это сумма энтропий для каждого подмножества, взятая со своим весом. Общая разница описывает, как уменьшится энтропия, сколько мы сэкономим бит для кодирования класса случайного объекта из набора X, если мы знаем значения атрибута A и разобьем набор данных на подмножества по данному атрибуту.

Алгоритм выбирает атрибут, соответствующий максимальному значению прироста информации.

Когда атрибут выбран, исходный набор разбивается на подмножества в соответствии с его значениями, исходный атрибут исключается из анализа, процесс повторяется рекурсивно.

Процесс останавливается, когда созданные подмножества стали достаточно однородны (преобладает один класс), а именно когда max(Gain(X,A)) становится меньше некоторого заданного параметра Θ (величина, близкая к 0). Как альтернативный вариант, можно контролировать само множество X, и когда оно стало достаточно мало или стало полностью однородным (только один класс), останавливать процесс.

Жадный алгоритм построения дерева решений

Более структурно алгоритм можно представить следующим образом:

1. Если max(Gain(X,A))

Источник

5.1.4. Анализ и решение задач с помощью дерева решений

Процесс принятия решений с помощью дерева решений в общем случае предполагает выполнение следующих пяти этапов.

Этап 1. Формулирование задачи. Прежде всего необходимо отбросить не относящиеся к проблеме факторы, а среди множества оставшихся выделить существенные и несущественные. Это позволит привести описание задачи принятия решения к форме, поддающейся анализу.

Должны быть выполнены следующие основные процедуры:

• определение возможностей сбора информации для экспериментирования и реальных действий;
• составление перечня событий, которые с определенной вероятностью могут произойти;
• установление временного порядка расположения событий, в исходах которых содержится полезная и доступная информация, а также тех последовательных действий, которые можно предпринять.

5.1.5. Пример процедуры принятия решения

Прототипом данного примера может служить реальный проект, реализованный в Москве. Пример 5.3. Руководство инвестиционной компании при выборе большого земельного участка для вложения своих (и привлеченных) средств решает:

• создавать ли на нем крупный культурно-оздоровительный комплекс с магазинами и предприятиями бытового обслуживания (проект «Аквадром»);
• вложить деньги в гаражное строительство (проект «Гараж»);
• отказаться от проекта вообще и использовать другие формы вложения денег (проект «Депозит»).

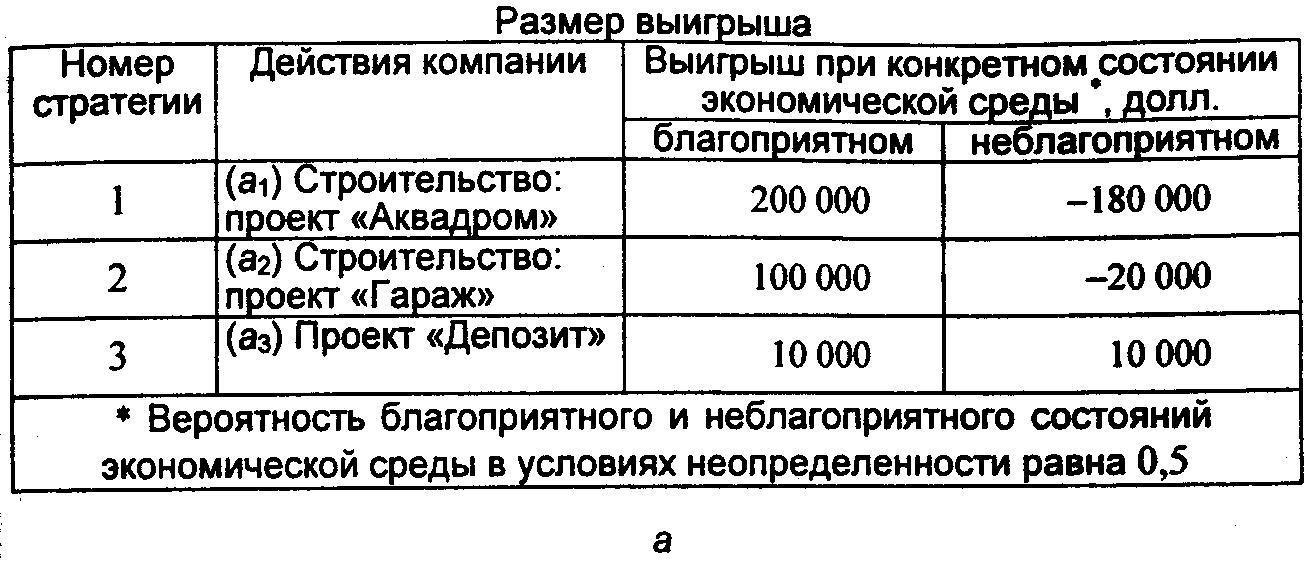
Размер выигрыша, который компания может получить, зависит от благоприятного или неблагоприятного состояния рынка городских услуг (рис. 5.1, а). На основе таблицы выигрышей (потерь) можно построить дерево решений (рис. 5.1, б).Процедура принятия решения заключается в вычислении для каждой вершины дерева (при движении справа налево) ожидаемых денежных оценок, отбрасывании неперспективных ветвей и выборе ветвей, которым соответствует максимальное значение ОДО. Определим средний ожидаемый выигрыш (ОДО). Результаты показаны в табл. 5.2. Таблица 5.2Определение ожидаемого выигрыша

Вершина	Расчетное выражение, долл.	Выигрыш, долл.
Вершина 1, ОДО1	0,5 •200 000 + 0,5 (-180 000)	10000
Вершина 2, ОД02	0,5 •100 000 + 0,5 (-20 000)	40000
Вершина 3, ОД03	—	10000

Вывод. Наиболее целесообразно выбрать стратегию а₂, т.е. выбрать проект «Гараж», а ветви (стратегии) a₁ и а₃ дерева решений можно отбросить. ОДО наилучшего решения равна 40 000 долл. Следует отметить, что наличие состояния с вероятностями 50 % неудачи и 50 % удачи на практике часто означает, что истинные вероятности игроку скорее всего неизвестны и он всего лишь принимает такую гипотезу (так называемое предположение fifty-fifty , т.е. «пятьдесят на пятьдесят»). Усложним рассмотренную выше задачу. Пусть, перед тем как принимать решение о строительстве (или об отказе от него), руководство компании должно определить, заказывать дополнительное исследование состояния рынка городских услуг или нет. Причем предоставляемая услуга обойдется компании в 10 000 долл. Руководство понимает, что дополнительное исследование по-прежнему не способно дать точной информации, но оно поможет уточнить ожидаемые оценки конъюнктуры рынка, изменив тем самым значения вероятностей. Относительно маркетинговой фирмы, которой можно заказать прогноз, известно, что она способна уточнить значения вероятностей благоприятного или неблагоприятного исхода. Возможности этой фирмы в виде условных вероятностей благоприятности и неблагоприятности рынка представлены на рис. 5.2, а. Например, когда фирма утверждает, что рынок благоприятный, то с вероятностью 0,78 этот прогноз оправдывается (с вероятностью 0,22 могут возникнуть неблагоприятные условия), прогноз о неблагоприятности рынка оправдывается с вероятностью 0,73. Предположим, что маркетинговая фирма, которой заказали прогноз состояния рынка, сделала следующий прогноз:

• ситуация будет благоприятной с вероятностью 0,45;
• ситуация будет неблагоприятной с вероятностью 0,55.

На основании дополнительных сведений можно построить новое дерево решений (рис. 5.2,6), где развитие событий происходит от корня дерева к исходам, а расчет прибыли выполняется от конечных состояний к начальным. Выводы. Необходимо проводить дополнительное исследование конъюнктуры рынка, поскольку это позволяет существенно уточнить принимаемое решение. Если фирма прогнозирует благоприятную ситуацию на рынке, то целесообразно выбрать проект «Аквадром» (ожидаемая максимальная прибыль 116 400 долл.), если прогноз неблагоприятный — проект «Гараж» (ожидаемая максимальная прибыль 12 400 долл.). Определим ожидаемую ценность точной информации. Предположим, что консалтинговая фирма за определенную плату готова предоставить информацию о фактической ситуации на рынке в тот момент, когда руководству компании надлежит принять решение о выборе проекта. Принятие предложения этой консалтинговой фирмы зависит от соотношения между ожидаемой ценностью (результативностью) точной информации и величиной запрошенной платы за дополнительную (истинную) информацию, благодаря которой может быть откорректировано принятие решения, т.е. первоначальное действие может быть своевременно изменено. Ожидаемая ценность точной информации о фактическом состоянии рынка равна разности между ожидаемой денежной оценкой при наличии точной информации и максимальной ожидаемой денежной оценкой при отсутствии точной информации. Рассчитаем ожидаемую ценность точной информации для примера, в котором дополнительное обследование конъюнктуры рынка не проводится. При отсутствии точной информации, как уже было показано выше, максимальная ожидаемая денежная оценка равна: ОДО = 0,5 • 100 000 — 0,5 • 20 000 = 40 000 долл. Если точная информация об истинном состоянии рынка будет благоприятной (ОДО = 200 000 долл., см. рис. 5.1, а), принимается решение в пользу проекта «Аквадром»; если неблагоприятной, то наиболее целесообразное решение — это проект «Депозит» (ОДО = 10 000 долл.). Учитывая, что вероятности благоприятной и неблагоприятной ситуаций равны 0,5, значение ОДО точной информации (ОДО_ти) определяется выражением: ОДО_т.и = 0,5 • 200 000 + 0,5•10 000 = 105 000 долл. Тогда ожидаемая ценность точной информации ОЦ_т.и равна: ОЦ_т.и = ОДО_т.и — ОДО = 105 000 — 40 000 = 65 000 долл. Значение ОЦ_т.и показывает, какую максимальную цену должна быть готова заплатить компания за точную информацию об истинном состоянии рынка в тот момент, когда ей это необходимо. При явной эффективности рассмотренной выше многоэтапной процедуры принятия решений следует отметить два обстоятельства, усложняющие ее применение на практике: 1) вероятности «ветвления» по дереву решений зачастую определяются экспертами консалтинговых фирм, причем необходимы дополнительные эксперты-аудиторы, которые оценивали бы надежность работы таких фирм; 2) прибыли (убытки) невозможно просчитать только по сметам бизнес-плана проекта; эти прибыли (убытки) зависят от сроков и динамики реализации проекта.

Источник