Статическое константное дерево на шаблонах C++
Поиск можно считать одной из наиболее нужных и часто используемых операций при разработке программного обеспечения. На сегодняшний день известно большое количество алгоритмов и структур данных, обеспечивающих высокую скорость поиска. Пусть и в меньшей степени, но подобные задачи возникают и в сфере разработки ПО для встраиваемых систем, одной из главных особенностей которой является существенная ограниченность системных ресурсов.
В статье предлагается рассмотреть особенности реализации элементарной структуры данных и способы оптимизации в условиях малого объема доступной памяти.
В процессе разработки фреймворка для ARM-микроконтроллеров мне захотелось реализовать более-менее универсальный способ обработки ответов устройств, управляемых посредством AT-команд.
Текущая идея заключается в реализации Patricia-дерева, где значениями узлов будут указатели на обработчики ответа, а ключами, соответственно, префиксы ответов. Однако классическая реализация выходит чересчур дорогой в плане расходования RAM, что заставило подумать над способами уменьшить количество необходимой памяти.
Префиксное дерево само по себе не самое простое для понимания и реализации, а если добавить шаблоны C++, то существует риск окончательно запутаться и не довести задумку до конца, поэтому экспериментировать я решил с BST.
Бинарное дерево поиска на C++
Классической структурой данных, предназначенной для быстрого поиска, является бинарное дерево поиска (BST – binary search tree), которое обладает следующими характеристиками:
- Временная сложность поиска: O (log n)
- Емкостная сложность: O(n)
И если с временной сложностью в целом поделать ничего нельзя (так как функция поиска элементарная) и реальное затраченное время зависит исключительно от размера данных и мощности процессора, то емкостная накладывает существенное ограничение на применимость данной структуры (да и других тоже) в условиях крайне малого объема доступной памяти.
Рассмотрим классическую реализацию бинарного дерева поиска на языке C++. В первую очередь необходимо определить тип данных каждого узла будущего дерева (для упрощения примем, что и ключи, и значения имеют целочисленный тип), код непосредственно реализации дерева можно опустить, так как с точки зрения расходования памяти он является несущественным, потому что содержит только указатель на корневой элемент:
Таким образом, каждый узел дерева занимает ~16 байтов (будем считать, что программа предназначена для 32-битных систем с размером указателя 4 байта и размером типа int также 4 байта), то есть константа в оценке емкостной сложности равна 16!
Подобная структура данных становится весьма дорогим удовольствием, учитывая размеры RAM современных микроконтроллеров. Например, один из самых популярных ARM-контроллеров низшей ценовой категории Stm32f103c8t6 предлагает 20 Кб RAM и 64 Кб Flash-памяти. Классическая реализация бинарного дерева поиска позволит хранить ~1200 узлов, что займет практически весь доступный объем оперативной памяти.
В то же время разработка программного обеспечения для микроконтроллерной техники имеет ряд особенностей, одной из которых можно считать нередкое отсутствие необходимости изменять структуру данных во время выполнения, значительная часть данных известна еще на этапе компиляции, что позволяет разместить их не в оперативной, а во flash‑памяти, используя приемы статического шаблонного программирования на языке C++.
Рассмотрим возможную модификацию реализации дерева.
Статическое константное дерево
Каждый узел дерева можно задать шаблонной структурой:
Несложно заметить, что структура содержит два статических константных значения, что позволяет ожидать от компилятора помещения их именно в ROM-память, а указатели на потомков заменены на их типы, то есть в памяти места не занимают.
В терминах шаблонных классов, когда каждый узел дерева определяет новый тип данных, понятие «текущий узел» (используемое в классической реализации метода поиска) некорректно, поскольку отсутствуют объекты. Вместо этого необходимо, как это обычно и происходит, применить рекурсивный алгоритм, добавив в структуру Node метод поиска:
static auto Search(unsigned key)
Само же дерево существенно упрощается, содержит только корень, а метод поиска делегирует поиск корневому элементу:
Основной проблемой является корректное формирование дерева на этапе компиляции, можно предложить три пути решения:
- Формировать узлы вручную.
- Написать программу генерации C++ кода с правильным порядком узлов (например, на каком-либо скриптовом языке).
- Используя приёмы метапрограммирования сформировать корректное дерево на этапе компиляции.
Может показаться, что первый и второй пункты добавлены для количества, однако признаюсь, что действительно первоначальной идеей было оставить все как есть и формировать узлы вручную.
Формирование структуры дерева в compile-time
Используемое в качестве примера бинарное дерево поиска с учетом изначально известного набора ключей несложно построить следующим алгоритмом:
- Корень дерева — это медианный элемент массива ключей.
- Левый потомок — это дерево из элементов левее медианного, правый — правее.
В рамках реализации автоматического построения дерева структура узла разделилась на 2 части:
/// Базовая структура (ключ-значение) template struct Node < static constexpr auto Key = _Key; static constexpr unsigned Value = _Value; >; /// Расширенный узел (с потомками) template struct ExtendedNode < static constexpr auto Key = _BaseNode::Key; static constexpr auto Value = _BaseNode::Value; using Left = _Left; using Right = _Right; static auto Search(unsigned key) < return key == Key ? Value : key < Key ? Left::Search(key) : Right::Search(key); >>;Пользователь объявляет необходимое количество базовых узлов, а специальный класс формирует из них по предложенному выше алгоритму дерево:
/// Компаратор узлов для их сортировки template struct NodesComparator < static const bool value = LeftNode::Key >RightNode::Key; >; /// Формирование узла template struct MakeNode < /// Сортировка узлов по ключам using SortedNodes = typename TypeListSort::type; static const int size = Length::value; /// Корень - медианный элемент, потомки формируются рекурсивно using type = ExtendedNode< typename GetType::type, typename MakeNode::type>::type, typename MakeNode::type>::type >; >; /// Дно рекурсии template<> struct MakeNode> < using type = NullNode; >;В коде выше использованы вспомогательные элементы из состава шаблонных утилит:
- TypeListSort — сортировка списка типов по предикату.
- GetType — получение типа из списка типов по его индексу.
- Slice — выбор среза из списка типов.
Для конечного пользователя формирование дерева выглядит так:
/// Объявить базовые узлы using N1 = Node; using N2 = Node; using N3 = Node; /// Объявить список узлов (не обязательно упорядочивать) using nodes = TypeList; /// Сформировать дерево using Tree = BST::type>; /// Поиск по дереву: Tree::Search(Value);Результаты
Предложенный подход проверен на компиляторе GCC для ARM, эксперименты с количеством узлов показали, что каждый узел дерева требует ~10 байтов ROM и ни одного байта RAM! (автор программирует под микроконтроллеры исключительно как любитель, но оперативная память, как правило, расходуется быстрее ROM).
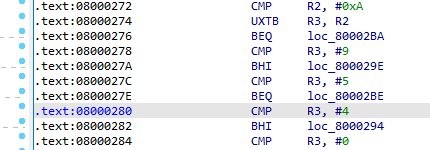
С точки зрения быстродействия программа также позволяет предположить максимальную скорость, поскольку поиск представляет собой последовательность конструкций if-else, фрагмент дизассемблированной версии программы приведен на рисунке 1, а более понятная декомпилированная версия – на рисунке 2.
Таким образом, если все элементы структуры данных известны на этапе компиляции, язык C++ позволяет существенно сэкономить ресурсы системы, объем занимаемой памяти сократился примерно в 1.6 раза, причем вся структура данных переместилась из RAM-памяти в ROM, что также можно считать позитивным результатом. Скорость поиска по сравнению с классической реализацией даже ускорится (честно признаюсь, не проверял, но смею заявить это на основании результатов дизассемблирования), так как переход по ветвям представляет собой просто последовательность условий.
Применимы ли полученные результаты на практике — вопрос для автора нерешенный. Как уже упоминалось под катом в начале, есть желание таким же образом реализовать префиксное дерево. Получится или нет — пока неизвестно. Однако сам эксперимент бы весьма интересным, позволил попрактиковаться в программировании на C++ и получить интересные результаты хотя бы в цифрах.
Источник
Создать шаблонный класс «бинарное дерево»
Создать шаблон класса «бинарное дерево». Использовать его для сортировки целых чисел и строк, задаваемых с клавиатуры или из файла.
Создать шаблонный класс «бинарное дерево»
Создать шаблон класса «бинарное дерево». Использовать его для сортировки целых чисел и строк.
Исходное бинарное дерево превратить в бинарное дерево поиска, при этом сохранив его структуру
Помогите, не могу понять!( Нужно исходное бинарное дерево превратить в бинарное дерево поиска, при.
Класс бинарное дерево
Здравствуйте. Требуется написать англо-русский словарь на основе бинарного дерева. Не полностью.
Описать класс, реализующий бинарное дерево
помогите ..ребят знаю что обсуждалось уже кучу раз..но у мне выдаёт ошибки..разобраться не.
Сообщение было отмечено Nikita123123 как решение
Решение
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237
#include #include #include #include #include templateclass T> class bstree { struct node { node* left; node* right; T val; node(void) noexcept :left(nullptr), right(nullptr){} }; private: node* tr; public: bstree(void) noexcept :tr(nullptr){} ~bstree() { clear(); } bstree(const bstree&) = delete; bstree& operator = (const bstree&) = delete; public: //добавить(только для уникальных значений) void add(const T& v){ node* p; if(tr == nullptr){ tr = new node(); tr->val = v; } else { node** rp = _find(v); if(tr != nullptr){ p = new node(); p->val = v; *rp = p; } } } void add(T&& v){ node* p; if(tr == nullptr){ tr = new node(); tr->val = std::forwardT>(v); } else { node** rp = _find(v); if(tr != nullptr){ p = new node(); p->val = std::forwardT>(v); *rp = p; } } } //удаление с возвращением min-значения T pop_min(void) noexcept { T v; node** rp = &tr, *p = tr; if(tr != nullptr){ while(p->left != nullptr){ rp = &p->left; p = p->left; } } if(p != nullptr){ v = std::forwardT>(p->val); _erase(rp, p); } return std::forwardT>(v); } //удаление с возвращением max-значения T pop_max(void) noexcept { T v; node** rp = &tr, *p = tr; if(tr != nullptr){ while(p->right != nullptr){ rp = &p->right; p = p->right; } } if(p != nullptr){ v = std::forwardT>(p->val); _erase(rp, p); } return std::forwardT>(v); } //удаление всех void clear(void) noexcept { _clear(tr); tr = nullptr; } bool empty(void) const noexcept { return (tr == nullptr); } private: node** _find(const T& v) noexcept { node** rp = &tr, *p = tr; while(p != nullptr){ if(v == p->val) return nullptr; else if(v p->val){ rp = &p->left; p = p->left; } else { rp = &p->right; p = p->right; } } return rp; } void _erase(node** rp, node* p) noexcept { if(p->right == nullptr) *rp = p->left; else { node* t = p->right; if(t->left == nullptr){ t->left = p->left; *rp = t; } else { node* i = t->left; while(i->left != nullptr){ t = i; i = t->left; } t->left = i->right; i->left = p->left; i->right = p->right; *rp = i; } } delete p; } void _clear(node* p) noexcept { if(p != nullptr){ if(p->left != nullptr) _clear(p->left); if(p->right != nullptr) _clear(p->right); delete p; } } }; /* чтение массива данных из строки, консоли или файла N = кол-во элементов данные . */ templatetypename T> void get_array(std::vectorT>& vs, std::istream& _in) } int main(void){ std::vectorint>::size_type i; //сортировка целых чисел std::vectorint> ia; /* ввод из консоли get_array(ia, std::cin);*/ // для примера ввод из строки char s[] = "10\n5 4 7 9 8 2 1 3 0 6"; std::istringstream sp(s); get_arrayint>(ia, sp); bstreeint> ti; for(auto v : ia) ti.add(v); for(i = 0; !ti.empty(); ++i) ia[i] = ti.pop_min(); for(auto v : ia) std::cout <' '; std::cout :: endl; //сортировка строк std::vectorstd::string> sa; //ввод из строки char s1[] = "7\nCOBOL\nJAVA\nFORTRAN\nERLANG\nFORTH\nALGOL\nBASIC"; std::istringstream sp1(s1); get_arraystd::string>(sa, sp1); bstreestd::string> ts; for(i = 0; i sa.size(); ++i) ts.add(std::move(sa[i])); for(i = 0; !ts.empty(); ++i) sa[i] = ts.pop_min(); for(const auto& v : sa) std::cout <' '; std::cout :: endl; //сортировка действительных чисел по убыванию std::vectordouble> da; /* ввод из файла std::ifstream fp("file.txt"); get_array(da, fp); fp.close(); */ //для примера из строки char s2[] = "5\n 0.9 20.5 -123.1 0.5 4.4"; std::istringstream sp2(s2); get_arraydouble>(da, sp2); bstreedouble> td; for(const auto& d : da) td.add(d); for(i = 0; !td.empty(); ++i) da[i] = td.pop_max(); for(const auto& v : da) std::cout <' '; std::cin.get(); return 0; } Источник