- Создание диаграммы «дерево» в Office
- Создание диаграммы «дерево»
- Изменение способа отображения меток
- Создание диаграммы «дерево»
- Дополнительные сведения
- Схема в форме дерева
- Метод аналогий для построения структурной схемы по электрической схеме
- Применение теории графов для построения структурной схемы системы
- Построение фундаментального дерева
- Получение матрицы связи, систем уравнений для напряжений и токов
- Получение структурной схемы
- Пример № 1
- Пример № 2
- Пример № 3
- Пример № 4
- Создание дерева решений (блок-схемы) в Excel. Инструмент «SmartArt».
- Пример дерева решений: «Поход в магазин за покупками»
- Создать такое дерево решений довольно просто при помощи кнопки SmartArt («умное творчество»).
- Добавить комментарий Отменить ответ
Создание диаграммы «дерево» в Office
Excel для Microsoft 365 Word для Microsoft 365 Outlook для Microsoft 365 PowerPoint для Microsoft 365 Excel для Microsoft 365 для Mac Word для Microsoft 365 для Mac Outlook для Microsoft 365 для Mac PowerPoint для Microsoft 365 для Mac Excel 2021 Word 2021 Outlook 2021 PowerPoint 2021 Excel 2021 для Mac Word 2021 для Mac Outlook 2021 для Mac PowerPoint 2021 для Mac Excel 2019 Word 2019 Outlook 2019 PowerPoint 2019 Excel 2019 для Mac Word 2019 для Mac Outlook 2019 для Mac PowerPoint 2019 для Mac Excel 2016 Word 2016 Outlook 2016 PowerPoint 2016 Excel 2016 для Mac Word 2016 для Mac PowerPoint 2016 для Mac Excel для iPad Excel для iPhone Еще. Меньше
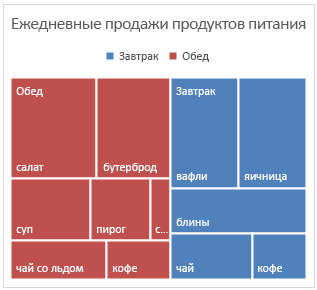
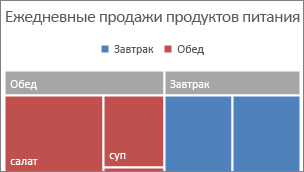
Диаграмма «дерево» обеспечивает иерархическое представление данных и позволяет легко определить закономерности, например то, какие элементы лучше всего подеются в магазине. Ветви дерева представлены прямоугольником, а каждая ветвь — как меньший прямоугольник. На диаграмме «дерево» категории отображаются по цвету и близости, а также могут легко отображать большое количество данных, что будет сложно сделать с другими типами диаграмм.
Диаграмма «дерево» удобна, если нужно сравнить пропорции в иерархии, но не очень хорошо отображает иерархические уровни между крупнейшими категориями и каждой точкой данных. Для этого намного больше подходит диаграмма «солнечные лучи».
Создание диаграммы «дерево»
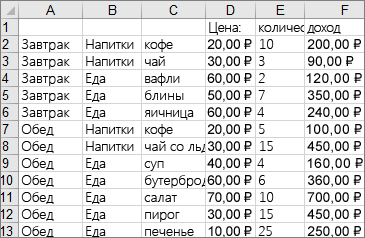
- Выделите данные.
- Перейдите на вкладку Вставка >вставить иерархическую диаграмму >дерево. Рекомендуемые диаграммы также можно использовать для создания диаграммы «дерево», на вкладке Вставка >Рекомендуемые диаграммы >всех диаграмм.
Совет: На вкладке Конструктори Формат можно настроить внешний вид диаграммы. Если эти вкладки не вы увидите, щелкните в любом месте диаграммы «дерево», чтобы активировать их.
Изменение способа отображения меток
Excel автоматически использует разные цвета для каждой категории верхнего уровня (родительской). Но вы можете дополнительно подчеркнуть различия между категориями с помощью макета меток данных.
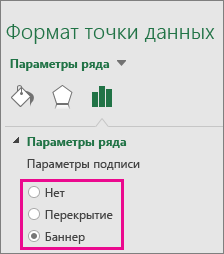
- Щелкните правой кнопкой мыши один из прямоугольников на диаграмме и выберите пункт Формат ряда данных.
- В разделе Параметры ряда >Параметры подписи выберите нужный параметр отображения.
Создание диаграммы «дерево»
- Выделите данные.
- На ленте на вкладке Вставка нажмите кнопку
(значок иерархии) и выберите дерево.
Примечание: На вкладке Конструктори Формат можно настроить внешний вид диаграммы. Если эти вкладки не вы увидите, щелкните в любом месте диаграммы «дерево», чтобы активировать их.
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
Источник
Схема в форме дерева
Для моделирования систем различной физической природы (электрических, механических, поступательно-вращательных, тепловых и т.д.) можно эффективно использовать метод физических аналогий.
Состояние эквивалентной схемы в любой момент времени характеризуется переменными двух типов: «поток» и «потенциал», а также уравнениями связи между ними. Для потоков и потенциалов используются соответствующие уравнения (аналог 1 и 2 законам Кирхгофа).
Для получения математических моделей подсистем различной физической природы необходимо:
1. Составить с учетом физических законов эквивалентную схему, используя компонентные и топологические уравнения, при этом выделяются аналогии массовых элементов в виде двухполюсников, один узел которых связан с системой отсчета, через другой осуществляется взаимодействие. Выделяются элементы трения и упругие элементы. Необходимо четко оговаривать допущения, при этом внешние воздействия (источники тока, потока, ЭДС) считаются заданными.
2. По эквивалентной схеме составляется структурная схема. Целесообразно составлять схему таким образом, чтобы не было дифференцирующих элементов. Если они появляются, нужно учесть дополнительные факторы, которые его погасят, либо использовать теорию графов. Топологические вырождения появляются, если имеются индуктивные сечения и емкостные контура.
3. После составления структурной схемы осуществляется моделирование и анализ полученных результатов.
Для получения математических моделей сложных подсистем различной физической природы необходимо:
1. Выделить соответствующие подсистемы.
2. Составить эквивалентные схемы.
3. Установить связь между подсистемами.
4. На основе эквивалентных схем составить структурные схемы.
5. По структурной схеме выполнить моделирование.
Для выполнения такого перехода применяется метод аналогий, который как метод моделирования систем различной физической природы основан на замещении типовых элементов схем на звенья структурной схемы системы с учётом протекающих в них процессов.
Метод аналогий для построения структурной схемы по электрической схеме
Аналоги электрических элементов, а также их уравнения, представлены на рисунке.
Источник напряжения E (ЭДС) и источник тока J на структурной схеме принимаются за внешние воздействия с соответствующими величинами. Для электрической схемы составляются уравнения токов и напряжений, а их суммы реализуются при помощи структурных элементов типа «сумматор». Полученная структурная схема должна быть замкнутой и содержать все электрические элементы.
Применение теории графов для построения структурной схемы системы
Получение структурной схемы по эквивалентной схеме удобно осуществить при помощи использования теории графов, которая содержит алгоритмы и методы, позволяющие строить по эквивалентным схемам (аналог электрической принципиальной схемы) систем описание в виде совокупности дифференциальных и алгебраических уравнений.
Граф – это совокупность вершин (узлов) и связей между ними в виде ребер (ветви). Совокупность ветвей образует маршрут. Замкнутый круг возникает, если маршрут начинается и заканчивается в том же узле.
Для получения дифференциальных и алгебраических уравнений необходимо строить фундаментальное дерево, в которое входят все узлы и соответствующие ветви без образования замкнутых контуров. При построении фундаментального дерева все электрические элементы заменяются ветвями и хордами с соответствующими направлениями. Хорда – это ветвь, включение которой между узлами приведёт к замыканию. Совокупность ветвей, которые окажутся замкнутыми хордой, называется контуром хорды.
Построение фундаментального дерева
При построении дерева выделяются и нумеруются узлы – места соединения электрических элементов. Если между узлами имеется идеальная связь (нет элемента), то эти узлы рассматриваются как один узел. Далее последовательно рассматриваются элементы коллекций E, C, R, L, I на возможность получения статуса ветви, а не хорды. Если в фундаментальном дереве можно соединить два узла, принадлежащих рассматриваемому элементу, без замыкания контура, то элемент имеет статус ветви. В противном случае элемент рассматривается как хорда.
Для каждой ветви и хорды задаётся направление, соответствующее направлению протеканию по ним тока. Он всегда направлен вверх (или вправо) от источника ЭДС или источника тока. В отличие от источника тока направление на самом источнике ЭДС имеет обратное направление (вниз, влево).
Так, для исследуемой эквивалентной электрической схемы, представленной на рисунке, фундаментальное дерево будет построено в последовательности E, R1, R2, L.
Получение матрицы связи, систем уравнений для напряжений и токов
Согласно полученному фундаментальному дереву с учётом направлений составляется матрица связей, в которой в строках записываются направления в контурах хорды, а в столбцах – ветви, входящие в этот контур. Если направление в ветви совпадает с направлением хорды, то связь положительная (+1), иначе связь отрицательная (–1). Если элемент не участвует в замыкании контура хордой, то его значение нейтрально (0).
Для рассматриваемого фундаментального дерева матрица связей имеет следующий вид:
Из методов теории графов следует, что напряжения на хордах и токи в ветвях взаимосвязаны с матрицей связей. Эти связи выражены в следующих уравнениях:
С учётом приведённых формул формируются соответствующие уравнения для рассматриваемой системы:
Системы уравнений для напряжений и токов в матричной форме раскрываются и используются при составлении структурной схемы исследуемой системы:
Получение структурной схемы
Построение структурной схемы системы по уравнениям рекомендуется производить в следующем порядке. Сначала в модель системы включаются внешние воздействия, соответствующие источникам напряжения и токов, а затем сумматоры, выходы которых считаются известными, соответствующими и равными уравнениям, в которых имеются несколько слагаемых. Далее в зависимости от типа электрического элемента добавляются блоки, выходы которых считаются известными. После этого известные выходы звеньев соединяются с соответствующими известными входами, а также реализуются остальные уравнения токов и напряжений.
В результате для исследуемой системы будет получена структурная схема:
Пример № 1
Исследуемая система представлена на рисунке и состоит из источника ЭДС, трёх ёмкостей, шести сопротивлений, трёх индуктивностей и источника тока. Направления движения тока сначала проставляются в контурах с источниками ЭДС и тока, а затем направления указываются на остальных элементах с учётом законов Кирхгофа: алгебраическая сумма токов в узле равна нулю, причём входящий в узел ток записывается с положительным знаком, а выходящий ток – с отрицательным.
Фундаментальное дерево для рассматриваемой схемы строится в следующей последовательности: E1, C1, C2, C3 — ветви; С4 — хорда; R1, R2 — ветви; R3 — хорда; R4, R5, R6, L1 — ветви; L2, L3, J1 — хорды. Тогда полученное фундаментальное дерево имеет следующий вид:
По полученному фундаментальному дереву составляется матрица связей, которая представлена в графической форме на рисунке:
Пример № 2
Исследуемая эквивалентная схема представлена на рисунке
Фундаментальное дерево для рассматриваемой системы представлено на рисунке и содержит ветви E1, C1, C2, R2, а также хорды R1, L1, J1.
По фундаментальному дереву составляется матрица связей и записываются системы уравнений для токов и напряжений, которые имеют следующий вид:
По полученным уравнениям строится структурная схема системы, которая представлена на рисунке:
Пример № 3
Исследуемая эквивалентная схема представлена на рисунке
Фундаментальное дерево для рассматриваемой системы представлено на рисунке и содержит ветви E1, C1, C2, R1, R2, а также хорды L1, L2, J1.
По фундаментальному дереву составляется матрица связей и записываются системы уравнений для токов и напряжений, которые имеют следующий вид:
По полученным уравнениям строится структурная схема системы, которая представлена на рисунке:
Пример № 4
Исследуемая эквивалентная схема представлена на рисунке
Фундаментальное дерево для рассматриваемой системы представлено на рисунке 30 и содержит ветви E1, C1, C2, C3, R1, R2, R3, а также хорды L1, L2, J1.
По фундаментальному дереву составляется матрица связей и записываются системы уравнений для токов и напряжений, которые имеют следующий вид:
По полученным уравнениям строится структурная схема системы, которая представлена на рисунке:
Все материалы сайта принадлежат лично Василию Щербакову.
Допускается использование материалов в некоммерческих или учебных целях с указанием ссылки на этот сайт.
Источник
Создание дерева решений (блок-схемы) в Excel. Инструмент «SmartArt».
Добрый день.
Как Вы наверняка знаете «Excel» — это не только инструмент для математических расчетов и аналитики числовых данных, но и прекрасный инструмент для оформления документов и создания схем взаимодействия (бизнес-схем).
В поздних версиях программы «Excel» созданы специальные опции для создания и редактирования древовидных схем (план-схем, алгоритмов). Таких как, так называемое, дерево решений.
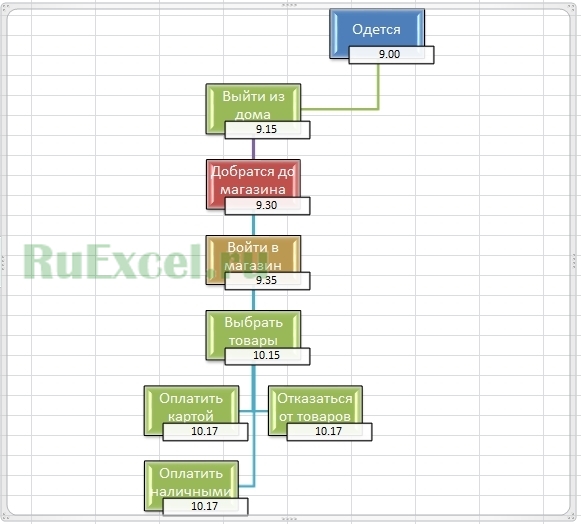
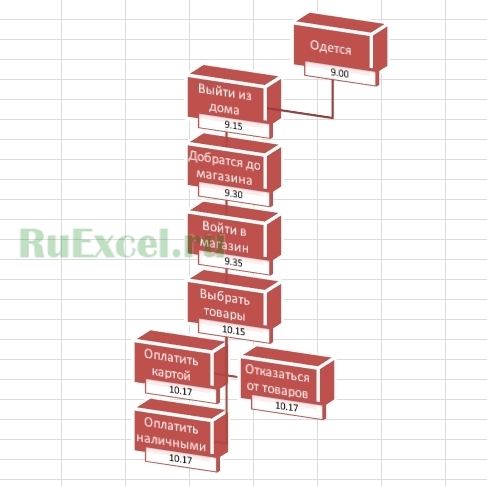
Дерево решений – это схема, представляющая собой набор связанных между собой в виде дерева блоков. Каждому из блоков в дереве решений присваивается действие (решение). Соответственно, при выполнении того или иного действия появляются несколько вариантов новых решений и т.д.
Пример дерева решений: «Поход в магазин за покупками»

Создать такое дерево решений довольно просто при помощи кнопки SmartArt («умное творчество»).
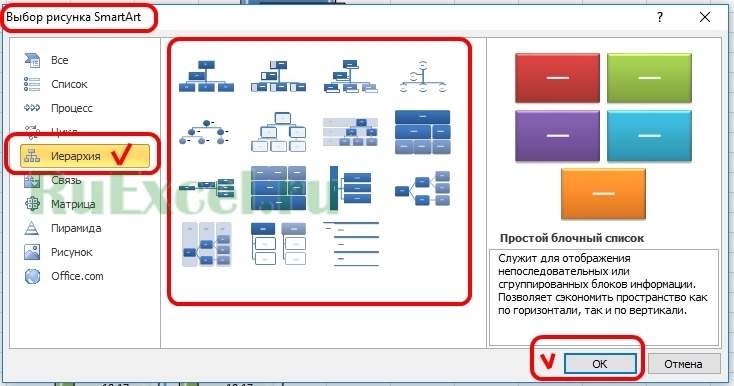
Кнопка SmartArt находится во вкладке «Вставка». После клика по указанной кнопке появляется окно, в котором предложены десятки готовых решений (структур) схемы.
Для дерева решений оптимально подходят готовые структуры и раздела «Иерархия».
Выбрав понравившуюся структуру, при помощи опций из вкладки «Конструктор» можно сформировать необходимой дерево действия.
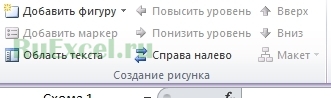
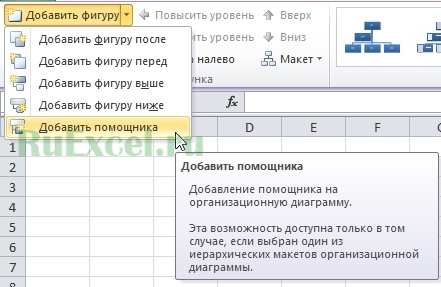
При помощи кнопки «Добавить фигуру» можно добавлять новые блоки.
Кнопками «повысить уровень» и «понизить уровень» можно менять место блока в структуре.
Кнопка «Область текста» открывает окно для работы с надписями в блоках.
Так же раздел «конструктор» позволяет редактировать внешний вид блоков:
Способ отображения блоков, в том числе и 3D вид дерева решений.
Добавить комментарий Отменить ответ
Этот сайт использует Akismet для борьбы со спамом. Узнайте, как обрабатываются ваши данные комментариев.
Источник
 (значок иерархии) и выберите дерево.
(значок иерархии) и выберите дерево.