7 Древовидные структуры данных
В задачах различного рода данные могут быть связаны между собой, не только образуя линейную последовательность (по горизонтали), но и иерархически (по вертикали, т.е. находиться на разных уровнях). Отношения типа предок-потомок являются иерархическими, тогда как брат-сестра — на одном уровне. Или такая иерархия:
Деревом называется структура, которая характеризуется следующими свойствами:
- существует единственный элемент, на который не ссылается никакой другой элемент. Этот элемент называется корнем.
- каждый элемент связан с несколькими элементами следующего уровня иерархии. Эти элементы могут быть в свою очередь деревьями (поддеревьями).
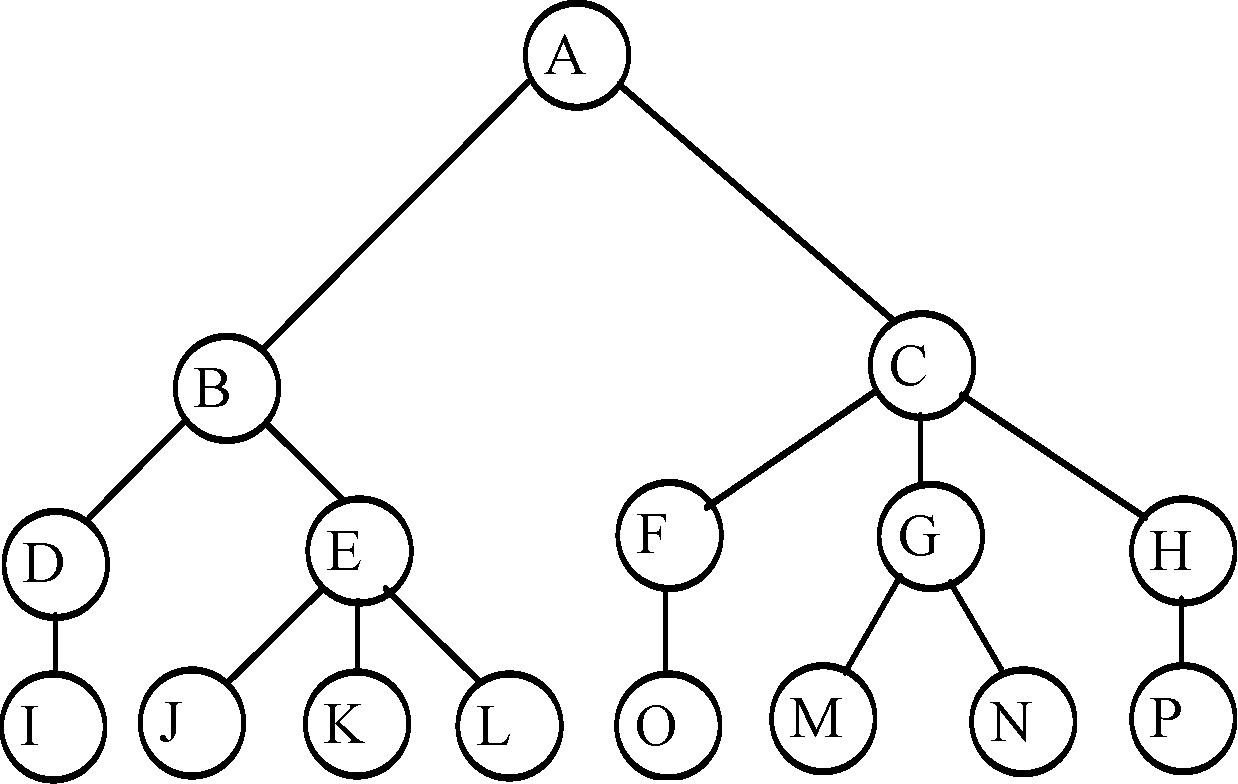
3)каждый элемент промежуточного уровня порожден только одним элементом более высокого уровня. Элементы дерева, которые не ссылаются на другие элементы, являются терминальными (т.е. конечными) или листьями. А элементы, не являющиеся терминальными, называются внутренними узлами. Таким образом дерево отражает иерархически упорядоченную структуру данных, в которой прослеживаются связи между элементами предыдущего (верхнего) уровня или предками и элементами следующего уровня — потомками. Можно считать список деревом, у которого каждый узел имеет не более одного «поддерева». Поэтому список называется также «вырожденным деревом». Существует несколько способов изображения древовидной структуры. Например, пусть базовый тип Т есть множество букв. Древовидную структуру, образованную с какой-либо целью на таком типе можно изобра- зить, например: а) вложенными множествами (рис. 17);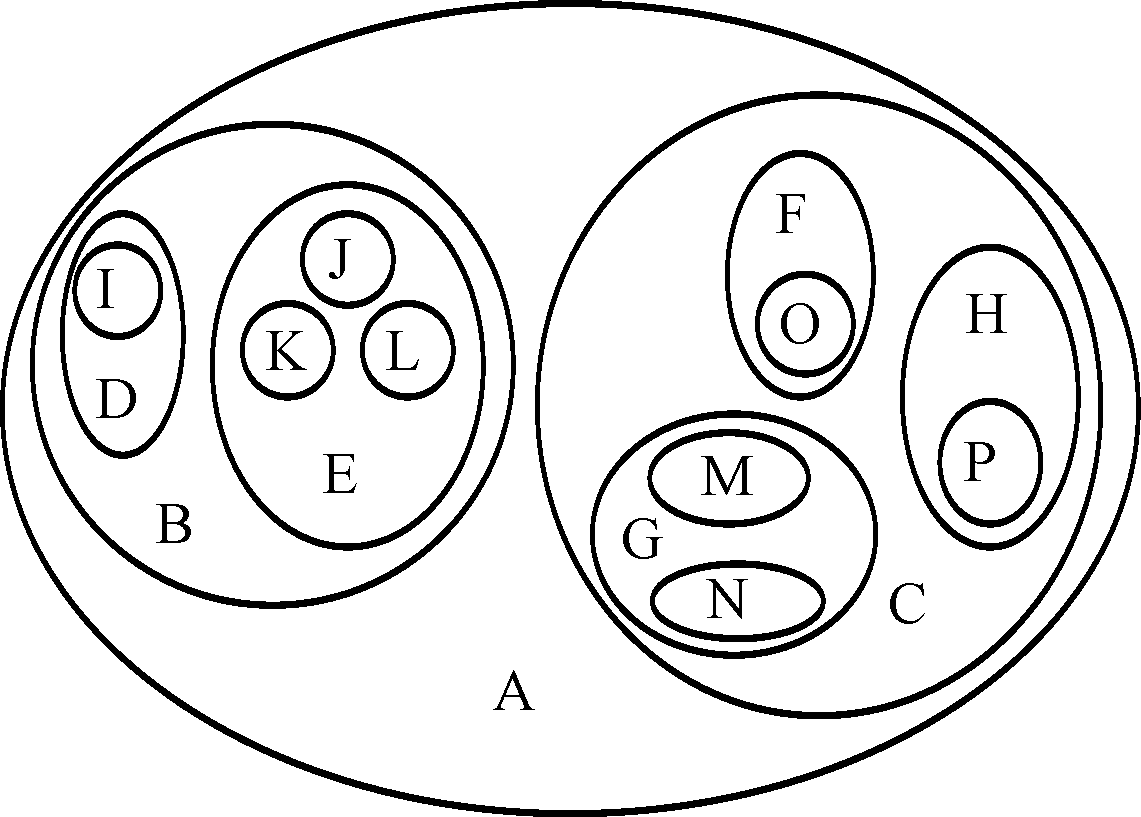 
Рис. 17 б)вложенными скобками (A(B(D(I), E(J, K, L)), C(F(O), G(M, N), H(P) ))); в)графом (рис. 18). 
Рис. 18 Графом дерево представляется нагляднее, но вверх ногами (корнем). Узлы располагаются по уровням. Корень – нулевой уровень и т.д. Максимальный уровень какого-либо элемента дерева называется его глубиной или высотой. Число непосредственных потомков внутреннего узла называется его степенью. Максимальная степень всех узлов есть степень дерева. Наше дерево – дерево третьей степени. Число ветвей или ребер, которые нужно пройти, чтобы продвинуться от корня к узлу х, называется длиной пути к х. Корень имеет длину пути 0, его непосредственные потомки – длину пути 1 и т.д. Вообще узел на уровне i имеет длину пути i. Длина пути дерева – это сумма длин путей всех его узлов. Она также называется длиной внутреннего пути. Для нашего дерева длина пути равна 36. Средняя длина пути 1 PcсрПHni-i=\ где ni – число узлов на уровне i; n – число элементов. Дерево, у которого ветви каждого узла упорядочены, называется упорядоченным деревом: 
разные упорядоченные деревья Особо важную роль играют упорядоченные деревья второй степени. Они называются бинарными деревьями или двоичными. Бинарное дерево – это конечное множество элементов (узлов), каждый из которых либо пуст (не связан с нижним уровнем, не имеет потомков, т.е. лист), либо является корнем (или узлом) с двумя различными бинарными поддеревьями – левым и правым. Деревья, имеющие степень больше двух, называются сильно ветвящимися деревьями. Пример бинарного дерева – Арифметическое выражение с двуместными операциями, где каждая операция – это ветвящийся узел с операндами в качестве поддеревьев, например выражение (a + b / c) * (d — e * f), представится в виде двоичного дерева следующим образом 
В принципе, любое n–арное дерево может быть преобразовано в эквивалентное ему бинарное дерево.
Источник
Сильно ветвящиеся деревья. B-деревья. Включение-исключение элементов
Сильно ветвящимися называются такие деревья ( структура данных в информатике, эмулирующая древовидную структуру в виде набора связанных узлов), у которых узлы имеют больше двух потомков. Простейший пример — генеалогическое древо, построенное по нисходящей, где у каждого человека может быть несколько детей, больше двух.
Если есть ограничение на максимальное количество детей узла дерева, можно представить детей в виде массива в записи узла. Однако, если количество детей у разных узлов отличается и далеко от максимума — это приведет к неэффективному расходованию памяти.
В общем случае, потомков следует располагать в виде линейного списка, а в узле хранить запись на его начало. Пример возможного описания:
Здесь узел имеет ссылку на своих «родственников» (т. е., вершины, с которыми у него общий родитель), а также на первый дочерний узел (который и содержит ссылки на все остальные).
Важная область применения таких деревьев — крупномасштабные деревья поиска, в которых нужны включения и удаления, однако их нельзя целиком загружать в ОЗУ, т. к. она не достаточно велика, либо дорого стоит. Соответственно, такие деревья хранятся на внешних накопителях, например, на дисках.
Принципиальное отличие здесь — адрес узла представляет собой адрес на диске, а не в памяти.
Если множество данных, состоящее, например, из миллиона элементов, хранится в виде бинарного дерева, то для поиска элемента потребуется в среднем около log2 10 6 = 20 шагов поиска. Поскольку теперь каждый шаг включает обращение к диску, будет весьма желательна организация памяти, требующая меньше обращений. Сильно ветвящееся дерево является идеальным решением этой проблемы. Если происходит обращение к некоторому одиночному элементу, расположенному на внешнем устройстве, то без больших дополнительных затрат можно обращаться также к целой группе элементов. Отсюда следует, что дерево нужно разделить на поддеревья, считая, что все эти поддеревья одновременно полностью доступны. Такие поддеревья называют страницами.
Уменьшение количества обращений к диску – а теперь обращение к каждой странице предполагает обращение к диску – может быть значительным. Предположим, что мы решили помещать на странице 100 узлов, тогда дерево поиска, содержащее миллион элементов, потребует в среднем только log100 10 6 = 3 обращений к страницам вместо 20. Но, конечно, если дерево растет «случайным образом», то наихудший случай может потребовать даже 10 4 обращений! Понятно, что в случае сильно ветвящихся деревьев почти обязательна схема управления их ростом.
При поиске критерия управляемого роста необходимо отвергнуть идеальную сбалансированность, так как она требует слишком больших затрат. Разумный критерий был сформулирован Р. Бэйром: каждая страница (кроме одной) содержит от n до 2n узлов при заданном постоянном n. Следовательно, в дереве с N элементами и максимальным размером страницы 2n узлов наихудший случай потребует logn N обращений к страницам. Кроме того, коэффициент использования памяти составляет не хуже 50%. Рассматриваемые структуры данных называются B-деревьями и имеют следующие свойства:
1. Каждая страница содержит не более 2n элементов.
2. Каждая страница, кроме корневой, содержит не менее n элементов.
3. Каждая страница является либо листом, т.е. не имеет потомков, либо имеет m + 1 потомков, где m – число находящихся на ней ключей.
4. Все листья находятся на одном и том же уровне.
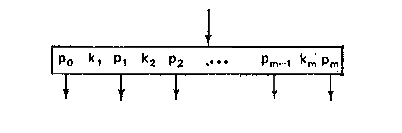
Сформулируем описание страницы (рис. 26).
Рисунок 26 — Страница В-дерева
На рисунке 27 показано Б-дерево порядка 2 с тремя уровнями. Все страницы содержат 2, 3 или 4 элемента. Исключением является корень, которому разрешается содержать только один элемент. Все листья находятся на уровне 3. Ключи расположены в возрастающем порядке слева направо, если спроектировать дерево на один уровень, вставляя потомков между ключами, находящимися на странице-предке. Такое расположение представляет естественное развитие принципа организации бинарных деревьев поиска и определяет метод поиска элемента с заданным ключом. Рассмотрим страницу, имеющую вид, как показано на рис. 26, и пусть задан аргумент поиска х. Предполагая, что страница считана в оперативную память, мы можем использовать известные методы поиска среди ключей k1, . km. Если т достаточно велико, можно применить бинарный поиск(деление на половины), если оно сравнительно небольшое, подойдет простой последовательный поиск. (Заметим, что время, требующееся для поиска в оперативной памяти мало по сравнению со временем, которое занимает считывание страницы с внешнего устройства.)
Рисунок 27 — Б-дерево порядка 2 с тремя уровнями
Если поиск неудачен, мы имеем одну из следующих ситуаций:
Если в каком-то случае ссылка равна nil, т. е. нет соответствующего потомка, то элемента с ключом х нет во всем дереве и поиск заканчивается.
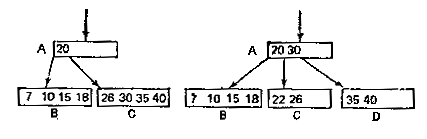
1. Выясняется, что ключ 22 отсутствует. Включение в страницу С невозможно, так как С уже заполнена.
2. Страница С расщепляется на две страницы, т. е. размещается новая страница D.
3. Количество m+1 ключей поровну распределяется на С и D, a средний ключ перемещается на один уровень вверх, на страницу-предка А.
Рисунок 28 — Включение ключа 22 в Б-дерево порядка 2
Эта схема сохраняет все основные свойства Б-деревьев. В частности, при расщеплении получаются страницы, содержащие ровно n элементов. Разумеется, включение элемента в страницу-предка может вновь вызвать переполнение этой страницы, что приведет к распространению расщепления. В экстремальном случае оно может распространиться до корня. Это и есть единственный случай увеличения высоты Б-дерева. Следовательно, Б-дерево растет странным способом: от листьев к корню.
Удаление элементов из Б-дерева очень просто в общих чертах, но сложно в деталях. Мы можем выделить два различных случая:
1. Элемент, который нужно удалить, находится на странице-листе; тогда алгоритм удаления прост и очевиден.
2. Этот элемент не на странице-листе; тогда его нужно заменить на один или два лексикографически смежных элемента, которые находятся на страницах-листьях и которые легко удалить.
В случае 2 поиск смежного ключа аналогичен поиску такого же ключа при удалении из бинарных деревьев. Мы спускаемся по самым правым указателям вниз к листу Р, заменяем удаляемый элемент на самый правый элемент Р и затем уменьшаем размер Р на 1.
Разумеется, может оказаться, что с Q нельзя забирать элементы, так как она тоже уже достигла своего минимального размера n. В этом случае общее число элементов на Р и Q равно 2n-1 и мы можем слить эти две страницы в одну, добавив средний элемент со страницы-предка Р и Q, а затем можем полностью располагать страницей Q. Это – процесс, в точности обратный расщеплению страниц.
Удаление среднего ключа на странице-предке может вновь уменьшить ее размер ниже допустимой границы n, требуя тем самым дальнейших специальных мер (балансировки или слияния) на более высоком уровне. В экстремальном случае слияние страниц может распространиться по всему пути к корню. Если корень уменьшается до размера 0, он удаляется, что вызывает уменьшение высоты Б-дерева. Это единственный случай, когда высота Б-дерева может уменьшиться.
На рисунке 30 показан постепенный распад Б-дерева с рисунка 29 при последовательном удалении ключей:
25 45 24; 38 32; 8 27 46 13 42; 5 22 18 26; 7 35 15.
Точки с запятой снова указывают места «скачков», т. е. освобождения страниц.
Рисунок 30 — Распад Б-дерева
Источник