Симметричная прошивка бинарного дерева

Что такое прошивка в бинарном дереве поиска?

Честно говоря, впервые услышал от вас такой термин. С одной стороны, материал по теме легко ищется, но я не знаю, стоит ли его писать как «ответ» (и вообще праивльный ли это ответ) khpi-iip.mipk.kharkiv.edu/library/datastr/book/prt06.html

@Lol4t0, думаю можете сделать ответом. Ведь в этом материале есть довольно подробный раздел ПРОШИВКА БИНАРНЫХ ДЕРЕВЬЕВ (и даже с массой картинок)

2 ответа 2

Под прошивкой дерева понимается замена по определенному правилу пустых указателей на сыновей указателями на последующие узлы, соответствующие обходу.

Прошивка делается для того, чтобы ускорить проход по дереву, переходя от листьев сразу на следующие по правилу обхода вершины.

Рассматривая бинарное дерево, легко обнаружить, что в нем имеются много нулевых указателей. Действительно в дереве с N вершинами имеется ( N+1 ) нулевых указателей. Это незанятое пространство можно использовать для изменения представления деревьев. Пустые указатели заменяются указателями — «нитями», которые адресуют вершины дерева, и расположенные выше. При этом дерево прошивается с учетом определенного способа обхода. Например, если в поле left некоторой вершины P стоит нулевой укзаатель, то его можно заменить на адрес, указывающий на предшественника P, в соответствии с тем порядком обхода, для которого прошивается дерево. Аналогично, если поле right пусто, то указывается преемник P в соответствии с порядком обхода. Поскольку после прошивания дерева поля left и right могут характеризовать либо структурные связи, либо «нити», возникает необходимость различать их, для этого вводятся в описание структуры дерева характеристики левого и правого указателей (FALSE и TRUE).

Таким образом, прошитые деревья быстрее обходятся и не требуют для этого дополнительной памяти (стек), однако требуют дополнительной памяти для хранения флагов нитей, а также усложнены операции включения и удаления элементов дерева.

Ячейка прошитого дерева имеет вид

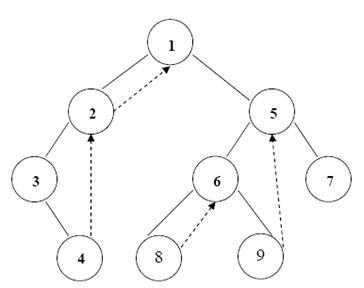
Прошитое дерево может выглядеть, например, следующим образом (нити показаны пунктиром)

Источник

6.2 Алгоритмы прошивки и обхода прошитых деревьев

Рассмотрим алгоритм правосторонней симметричной прошивки бинарного дерева.

1. Строится бинарное дерево. При этом поля ltagиrtagсоздаваемых узлов дерева остаются неопределенными, аleft иright соответственно указывают на левое или правое поддеревья, либо равныnil. На корень построенного дерева указываетroot.
2. Создается головной узел, left которого указывает на корень дерева, аright на сам головной узел:

1. Прошивка правых связей. Вводится дополнительный глобальный указатель y(указатель на узел, предшествующий текущему узлу). Указатель на текущий узелpустанавливаем на корень дерева (p := HEAD^.llink ).

1. Переход к корню дерева ( p := HEAD^.left).
2. До тех пор, пока p^.left<>nil, повторять:p := p^.left, то есть идти по левой ветви до самого левого узла.
3. Обработка узла p, например, печатьp^.info.
4. Если p^.rtag равенfalse, тоp := p^.right и переход к шагу 3 ( к преемнику). Иначеp:= p^.right и переход к шагу 2.

6.3 Лабораторная работа №6

Цель работы: научиться прошивать различными способами, а затем обходить бинарные деревья, а также выполнять на них операции с данными.

Порядок выполнения работы

1. Выполнить симметричную прошивку бинарного дерева поиска. Обойти его согласно симметричному порядку следования элементов. Реализовать вставку и удаление элементов из симметрично прошитого бинарного дерева.
2. Выполнить прямую прошивку бинарного дерева поиска. Обойти его согласно прямому порядку следования элементов. Реализовать вставку и удаление элементов из прямо прошитого бинарного дерева.

7. Поиск маршрутов на ориентированных графах

7.1 Основные определения ориентированных графов

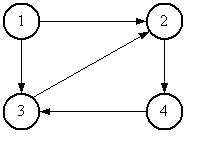
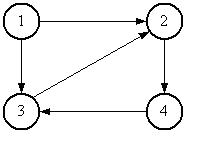
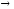
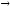
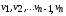
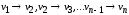
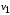
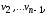
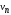
Ориентированный граф(или орграф)G=(V, E)состоит из множества вершинVи множества дугЕ. Вершины также называют узлами, а дуги – ориентированными ребрами. Дуга представляется в виде упорядоченной пары вершин(v, w), где вершинаvназывается началом, аw – концом дуги. Дугу(v, w) часто записывают какv wи изображают в виде Кроме того, дуга v wведет от вершиныvк вершинеw, а вершинаwсмежная с вершинойv. На рис. 7.1 показан орграф с четырьмя вершинами и пятью дугами. Рис. 7.1 – Пример орграфа Вершины орграф можно использовать для представления объектов, а дуги – для отношений между объектами. Например, вершины орграфа могут представлять города, а дуги – маршруты рейсовых полетов самолетов из одного города в другой. В виде орграфа может быть представлена блок-схема потока данных в компьютерной программе. В последнем примере вершины соответствуют блокам операторов программы, а дугам – направленное перемещение потоков данных. Путем в орграфе называется последовательность вершин, для которых существуют дуги. Этот путь начинается в вершинеи, проходя через вершинызаканчивается в вершине. Длина пути – количество дуг, составляющих путь, в данном случае длина пути равнаn–1. Одна вершина рассматривается как путь длины 0 от вершиныvк этой же вершинеv. Путь называется простым, если все вершины на нем, за исключением, может быть, первой и последней, различны. Цикл – это простой путь длины не менее 1, который начинается и заканчивается в одной и той же вершине. На рисунке 1 вершин 3, 2, 4, 3 образуют цикл длины 3. Во многих приложениях удобно к вершинам и дугам присоединить какую-либо информацию. Для этих целей используется помеченный граф, т.е. орграф, у которого каждая дуга и/или каждая вершина имеет соответствующие метки. Меткой может быть имя, вес или стоимость (дуги), или значение данных какого-либо заданного типа.

Источник

Прошитые бинарные деревья

В случае представления бинарного дерева в виде узлов, содержащих информационное поле и два поля связи, количество полей связи, имеющих значения nil, всегда больше числа связей, указывающих на реально существующие узлы. Поэтому часто такой способ хранения деревьев оказывается неэффективным с точки зрения использования памяти, особенно, если размер информационного поля сопоставим с размером указателя.

Эффективность прохождения дерева рекурсивными и нерекурсивными алгоритмами может быть увеличена, если использовать пустые указатели на отсутствующие поддеревья для хранения в них адресов узлов преемников, которые надо посетить при заданном порядке прохождения бинарного дерева. Такой указатель называется нитью. Его следует отличать от указателей в дереве, которые используются с левым и правым поддеревьями. Операция, заменяющая пустые указатели на нити, называется прошивка. Она может выполняться по-разному. Если нити заменяют пустые указатели в узлах с пустыми правыми поддеревьями, при просмотре в симметричном порядке, то бинарное дерево называется симметрично прошитым справа. Похожим образом может быть определено бинарное дерево, симметрично прошитое слева: дерево, в котором каждый пустой левый указатель изменен так, что он содержит нить – связь к предшественнику данного узла при просмотре в симметричном порядке. Симметрично прошитое бинарное дерево – это то, которое симметрично прошито слева и справа. Однако левая прошивочная нить не дает тех преимуществ, что правая прошивочная нить. На рис. 6.1 показано дерево, симметрично прошитое справа. На нем пунктирными линиями обозначены прошивочные нити.

Рис. 6.1 – Симметрично прошитое справа бинарное дерево

Также используются бинарные деревья, прямо прошитые справа и слева. В них пустые правые и левые указатели узлов заменены соответственно на их преемников и предшественников при прямом порядке просмотра. Прошитые деревья эффективно проходятся без использования стека.

Поскольку нужно каким-то образом отличать обычную связь от прошивочной нити, каждому узлу добавляется два однобитовых (логических) поля тэга: ltag и rtag. Если значение тэга true, соответствующее поле связи является обычной связью, в случае значения false – прошивочной нитью.

В этой связи узел обычного бинарного дерева представляется структурой

Узел прошитого бинарного дерева имеет иную структуру

Логические поля в прошитом дереве могут принимать следующие значения.

1. ltag=true, следовательно, left представляет собой обычную связь.

2. ltag=false, следовательно, left указывает на узел-предшественник.

3. rtag=true, следовательно, right представляет собой обычную связь.

4. rtag=false, следовательно, right указывает на узел-преемник.

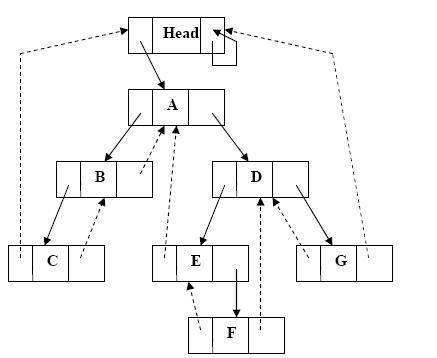
Рассмотрим вставку новой вершины слева от заданной в симметрично прошитое бинарное дерево (рис. 6.2). На рис. 6.3 показано результирующее дерево.

Рис. 6.2 – Исходное симметрично прошитое дерево

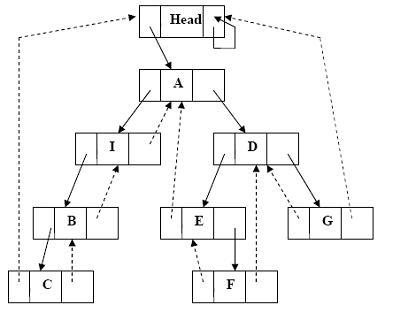
Рис. 5 – Прошитое дерево после вставки в него нового элемента

Здесь требовалось вставить вершину I вкачестве левого поддерева вершины А, если А не имеет левого поддерева. В противном случае новая вершина вставляется между А и ее левым сыном.

Для удобства создания и обхода дерева используется дополнительная головная вершина Head, которая служит при симметричном обходе предшественником его первой вершины и приемником всех его концевых вершин.

Наряду с преимуществами прошитых деревьев: быстрый обход, отсутствие необходимости в стеке, можно определить предшественника и преемника вершины, существуют недостатки. Включение новой вершины в дерево занимает больше времени, т.к. необходимо поддерживать два типа связей: структурные и по нитям. Поэтому прошитые деревья целесообразно использовать в тех задачах, где изменения в деревьях происходят редко, а обходы выполняется часто.

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:

Источник

6.2 Алгоритмы прошивки и обхода прошитых деревьев

Рассмотрим алгоритм правосторонней симметричной прошивки бинарного дерева.

1. Строится бинарное дерево. При этом поля ltagиrtagсоздаваемых узлов дерева остаются неопределенными, аleft иright соответственно указывают на левое или правое поддеревья, либо равныnil. На корень построенного дерева указываетroot.
2. Создается головной узел, left которого указывает на корень дерева, аright на сам головной узел:

1. Прошивка правых связей. Вводится дополнительный глобальный указатель y(указатель на узел, предшествующий текущему узлу). Указатель на текущий узелpустанавливаем на корень дерева (p := HEAD^.llink ).

1. Переход к корню дерева ( p := HEAD^.left).
2. До тех пор, пока p^.left<>nil, повторять:p := p^.left, то есть идти по левой ветви до самого левого узла.
3. Обработка узла p, например, печатьp^.info.
4. Если p^.rtag равенfalse, тоp := p^.right и переход к шагу 3 ( к преемнику). Иначеp:= p^.right и переход к шагу 2.

6.3 Лабораторная работа №6

Цель работы: научиться прошивать различными способами, а затем обходить бинарные деревья, а также выполнять на них операции с данными.

Порядок выполнения работы

1. Выполнить симметричную прошивку бинарного дерева поиска. Обойти его согласно симметричному порядку следования элементов. Реализовать вставку и удаление элементов из симметрично прошитого бинарного дерева.
2. Выполнить прямую прошивку бинарного дерева поиска. Обойти его согласно прямому порядку следования элементов. Реализовать вставку и удаление элементов из прямо прошитого бинарного дерева.

7. Поиск маршрутов на ориентированных графах

7.1 Основные определения ориентированных графов

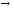
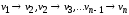
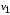
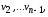
Ориентированный граф(или орграф)G=(V, E)состоит из множества вершинVи множества дугЕ. Вершины также называют узлами, а дуги – ориентированными ребрами. Дуга представляется в виде упорядоченной пары вершин(v, w), где вершинаvназывается началом, аw – концом дуги. Дугу(v, w) часто записывают какv wи изображают в виде Кроме того, дуга v wведет от вершиныvк вершинеw, а вершинаwсмежная с вершинойv. На рис. 7.1 показан орграф с четырьмя вершинами и пятью дугами. Рис. 7.1 – Пример орграфа Вершины орграф можно использовать для представления объектов, а дуги – для отношений между объектами. Например, вершины орграфа могут представлять города, а дуги – маршруты рейсовых полетов самолетов из одного города в другой. В виде орграфа может быть представлена блок-схема потока данных в компьютерной программе. В последнем примере вершины соответствуют блокам операторов программы, а дугам – направленное перемещение потоков данных. Путем в орграфе называется последовательность вершин, для которых существуют дуги. Этот путь начинается в вершинеи, проходя через вершинызаканчивается в вершине. Длина пути – количество дуг, составляющих путь, в данном случае длина пути равнаn–1. Одна вершина рассматривается как путь длины 0 от вершиныvк этой же вершинеv. Путь называется простым, если все вершины на нем, за исключением, может быть, первой и последней, различны. Цикл – это простой путь длины не менее 1, который начинается и заканчивается в одной и той же вершине. На рисунке 1 вершин 3, 2, 4, 3 образуют цикл длины 3. Во многих приложениях удобно к вершинам и дугам присоединить какую-либо информацию. Для этих целей используется помеченный граф, т.е. орграф, у которого каждая дуга и/или каждая вершина имеет соответствующие метки. Меткой может быть имя, вес или стоимость (дуги), или значение данных какого-либо заданного типа.

Источник