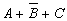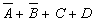Система логических уравнений дерево

Методы решения систем логических уравнений
статья по информатике и икт (10 класс) по теме

Решить систему логических уравнений можно, например, с помощью таблицы истинности (если количество переменных не слишком велико) или с помощью дерева решений, предварительно упростив каждое уравнение.

1. Метод замены переменных.

Ввод новых переменных позволяет упростить систему уравнений, сократив количество неизвестных. Новые переменные должны быть независимыми друг от друга . После решения упрощенной системы надо снова вернуться к первоначальным переменным.

Рассмотрим применение этого метода на конкретном примере.

Пример. Сколько различных решений имеет система уравнений

((X1 ≡ X2) ∧ (X3 ≡ X4)) ∨ (¬(X1 ≡ X2) ∧ ¬(X3 ≡ X4)) = 0

((X3 ≡ X4) ∧ (X5 ≡ X6)) ∨ (¬(X3 ≡ X4) ∧ ¬(X5 ≡ X6)) = 0

((X5 ≡ X6) ∧ (X7 ≡ X8)) ∨ (¬(X5 ≡ X6) ∧ ¬(X7 ≡ X8)) = 0

((X7 ≡ X8) ∧ (X9 ≡ X10)) ∨ (¬(X7 ≡ X8) ∧ ¬(X9 ≡ X10)) = 0

где x1, x2, …, x10 – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

Введем новые переменные: А=(X1 ≡ X2); В=(X3 ≡ X4); С=(X5 ≡ X6); D=(X7 ≡ X8); E=(X9 ≡ X10).

(Внимание! Каждая их переменных x1, x2, …, x10 должна входить только в одну из новых переменных А,В,С,D,Е, т.е. новые переменные независимы друг от друга).

Тогда система уравнений будет выглядеть так:

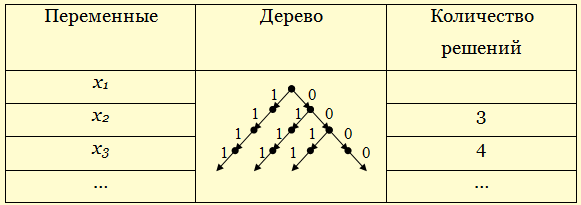
Построим дерево решений полученной системы:

Рассмотрим уравнение А=0, т.е. (X1 ≡ X2)=0. Оно имеет 2 корня:

Из этой же таблицы видно, что уравнение А=1 тоже имеет 2 корня. Расставим кол-во корней на дереве решений:

Чтобы найти количество решений одной ветви, надо перемножить количества решений на каждом ее уровне. Левая ветвь имеет 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2=32 решения; правая ветвь имеет тоже 32 решения. Т.е. вся система имеет 32+32=64 решения.

Сложность решения систем логических уравнений состоит в громоздкости полного дерева решений. Метод рассуждений позволяет не строить все дерево полностью, но понять при этом, сколько оно будет иметь ветвей. Рассмотрим этот метод на конкретных примерах.

Пример 1. Сколько существует различных наборов значений логических переменных x1, x2, x3, x4, x5, y1, y2, y3, y4, y5, которые удовлетворяют всем перечисленным ниже условиям?

(x1→x2) /\ (x2→x3) /\ (x3→x4) /\ (x4→x5 ) = 1

(y1→y2) /\ (y2→y3) /\ (y3→y4) /\ (y4→y5 ) = 1

В ответе не нужно перечислять все различные наборы значений переменных x1, x2, x3, x4, x5, y1, y2, y3, y4, y5, при которых выполнена данная система равенств. В качестве ответа Вам нужно указать количество таких наборов.

Первое и второе уравнения содержат независимые переменные, которые связаны третьим условием. Построим дерево решений первого и второго уравнений.

Чтобы представить дерево решений системы из первого и второго уравнений, надо каждую ветвь первого дерева продолжить деревом для переменных у . Построенное таким образом дерево будет содержать 36 ветвей. Некоторые из этих ветвей не удовлетворяют третьему уравнению системы. Отметим на первом дереве количество ветвей дерева «у» , которые удовлетворяют третьему уравнению:

Поясним: для выполнения третьего условия при х1=0 должно быть у1=1, т.е все ветви дерева «х» , где х1=0 можно продолжить только одной ветвью из дерева «у» . И только для одной ветви дерева «х» (правой) подходят все ветви дерева «у». Таким образом, полное дерево всей системы содержит 11 ветвей. Каждая ветвь представляет собой одно решение исходной системы уравнений. Значит, вся система имеет 11 решений.

Пример 2. Сколько различных решений имеет система уравнений

(X1 ≡ X2) ∨ (X1 ∧ X10) ∨ (¬X1 ∧ ¬ X10)= 1

(X2 ≡ X3) ∨ (X2 ∧ X10) ∨ (¬X2 ∧ ¬ X10)= 1.

(X9 ≡ X10) ∨ (X9 ∧ X10) ∨ (¬X9 ∧ ¬ X10)= 1

где x1, x2, …, x10 – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

Решение : Упростим систему. Построим таблицу истинности части первого уравнения:

Источник

Построение деревьев в алгебре логики

Логическую задачу можно решить: а) составляя систему логических уравнений; б) графическим способом.

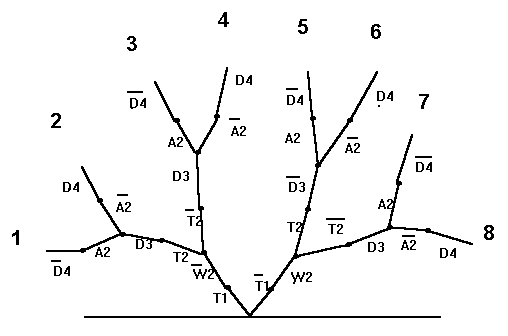
1. Решение логических задач с использованием систем логических уравнений. Задача 1. В соревнованиях по гимнастике на первенство школы участвуют Алла, Валя, Таня и Даша. Болельщики высказали предположения о возможных победителях: 1: “Первой будет Таня, Валя будет второй”. 2: “Второй будет Таня, Даша — третьей”. 3: “Алла будет второй, Даша — четвертой”. По окончании соревнований оказалось, что в каждом предположении только одно из высказываний истинно, другое же ложно. Какое место на соревнованиях заняла каждая из девочек, если все они оказались на разных местах? Решение. Введем буквенные обозначения всех высказываний, задающих условие задачи: T₁ — “Таня будет первой”; W₂ — “Валя будет второй”; T_{2 —} “Таня будет второй”; D_{3 —} “ Даша будет третьей”; A_{2 —} “ Алла будет второй”; D₄ — “Даша будет четвертой”. 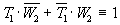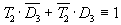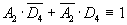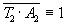Высказывание каждого болельщика о двух спортсменах можно задать формулами: (1) (2) (3) Помним, что в условии сказано: в каждом предположении только одно из высказываний истинно, другое ложно. Следует учесть и то, что ни одно место не было разделено участниками. Это условие можно задать формулами: A₂ W₂ 0 или (4) T₂ A₂0 или или (5) T₂ W₂ 0 или (6)

То обстоятельство, что ни один участник не может занять два разных места, задано формулами (7) и (8). D₃ D₄ 0 или (7) T₁ T₂ 0 или (8) Система уравнений решается умножением одного уравнения на другое и нахождением истинного выражения. Умножая уравнение (1) на (2), получим: (9) Умножаем полученное уравнение (9) на (3), получаем: Итак, мы получим ответ: Таня — первая; Валя — четвертая; Даша — третья; Алла — вторая.

2. Графический способ решения систем логических уравнений.

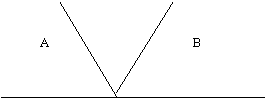
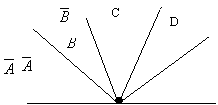
Рассматривая алгебру высказываний, мы сопоставляем ее с алгеброй чисел. Обратимся к сравнению еще раз. В школьной алгебре для решения уравнений и систем уравнений широко используется графический метод. В алгебре высказываний графические методы применяются не менее успешно. При решении логических задач очень часто полезно вычертить “дерево логических условий”. Это “дерево” выражает в виде простого чертежа логическую взаимосвязь между данными высказываниями. Научимся “выращивать” логические деревья на простых примерах. Выращивание любого дерева начинается с рассмотрения исходной формулы. Логической сумме на логическом дереве будет соответствовать “разветвление” ветвей. Логическому произведению на выращиваемом дереве будет соответствовать “следование” ветвей друг за другом. Пример 1. Построить дерево для высказывания А+В. Решение. Каждому простому высказыванию в формуле на выращиваемом дереве будет соответствовать одна ветвь.

Пример 2.

Пример 3.

Пример 4.

Пример 5.

Пример 6.

Пример 7.

Вернемся к условию задачи № 1, построим к ней графическое дерево и проанализируем каждую его ветвь. Для вычерчивания графического дерева нам понадобятся уравнения (1), (2), (3).

Проанализируем каждую ветвь. Ветвь 1: т.к. T₁ T₂ 0, A₂ T₂ 0 Ветвь 2: т.к. T₁ T₂ 0 Ветвь 3: Ветвь 4: , т.к. D₃ D₄  0 Ветвь 5: , т.к. W₂ T₂ 0, T₂ A₂ _ Ветвь 6: , т.к. W₂_{ 2} _ Ветвь 7: , т.к. W₂ _{ 2} _ Ветвь 8: , т.к. D₃ D₄  _ Итак, только выражение ветви 3 эквивалентно 1: Из этого выражения следует: Таня — первая; Алла — вторая; Даша — третья; Валя — четвертая.

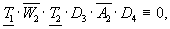
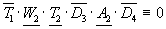
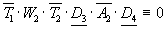
Источник

Система логических уравнений дерево

Предположим, что x1 – истинно, тогда из первого уравнения получаем, что x2 также истинно. Далее из второго уравнения получаем, что x3 истинно, и т.д. до xm = 1. Значит набор (1; 1; …; 1) из m единиц является решением системы.

Пусть теперь x1 – ложно, тогда из первого уравнения следует, что x2 может быть как истинным, так и ложным, то есть может принимать значения как 0, так и 1.

В случае, если x2 истинно получаем, что остальные переменные также истинны, то есть набор (0; 1; …; 1) является решением системы. В случае, когда x2 – ложно получаем, что для x3 есть две возможности, 0 и 1, и так далее. Продолжая до последней переменной, получаем, что решениями уравнения являются следующие наборы переменных (m+1 решение, в каждом решении по m значений переменных):

Такой подход хорошо иллюстрируется с помощью построения бинарного дерева. Получив единицу, все остальные значения переменных также становятся единицами, получив же ноль, возможны два варианта 0 и 1. Для одного уравнения дерево состоит из двух уровней, для двух уравнений добавляется одна переменная и соответственно один уровень дерева. Количество возможных решений – количество различных ветвей построенного дерева. Легко заметить, что оно равно m+1.

В случае трудностей в рассуждениях и построении дерева решений можно искать решение с использованием таблиц истинности, для одного – двух уравнений.

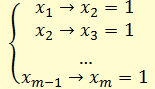
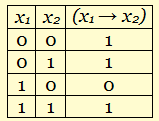
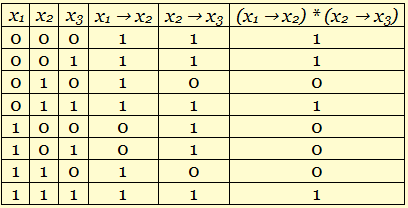
Система двух уравнений истина в четырех случаях (0; 0; 0), (0; 0; 1), (0; 1; 1), (1; 1; 1). При этом сразу видно, что существует решение, состоящее из одних нулей и еще m решений, в которых добавляется по одной единице, начиная с последней позиции до заполнения всех возможных мест. Можно предположить, что общее решение будет иметь такой же вид. Хотя это, конечно, не решение, но ответ таким образом угадать можно. Для того, чтобы такой подход стал решением, требуется доказательство, что предположение верно.

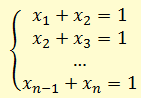
Решая систему, любым из вышеописанных методов, получим 5 различных решений: (0; 1; 0), (0; 1; 1), (1; 0; 1), (1; 1; 0), (1; 1; 1). Для системы из трех уравнений имеем 8 решений – (0; 1; 0; 1), (0; 1; 1; 0), (0; 1; 1; 1), (1; 0; 1; 0), (1; 0; 1; 1), (1; 1; 0; 1), (1; 1; 1; 0), (1; 1; 1; 1).

Проанализировав данную систему логических уравнений, можно сделать вывод: если первая переменная любого уравнения принимает значение 0, то вторая переменная этого же уравнения обязательно примет значение 1, в противном случае, произвольное значение 1 или 0.

Обозначим Nk – общее количество решений системы k уравнений, N_k^0, N_k^1 – количество решений этой системы, последняя переменная которых соответственно равна 0 или 1. Понятно, что N_1^0 = 1, N_1^1 = 2.

Для представленной системы, получаем такое рекуррентное соотношение, с начальными условиями N1 = 3, N2 = 5. Такому соотношению соответствуют числа Фибоначчи, то есть элементам числовой последовательности 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, …, в которой каждое последующее число равно сумме двух предыдущих чисел.

Сравнив начальные значения с последовательностью Фибоначчи, получаем, что количество различных решений равно (n+2)-му члену последовательности Фибоначчи Fn+2.

Источник