Смешанный обход бинарного дерева

Обход бинарного дерева

Методы обхода дерева любой степени, рассматриваемые в подразделе 10.3, переформулируем в отношении бинарных деревьев.

1. Нисходящий обход:

• обработка корня,
• нисходящий обход левого поддерева,
• нисходящий обход правого поддерева.

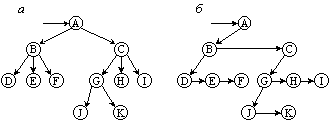
Вершины дерева, изображенного на рисунке 9.8, поступали бы на обработку при обходе нисходящим методом в следующем порядке: a, b, d, h, i, e, c, f, g, j.

1. Смешанный обход:

• смешанный обход левого поддерева,
• обработка корня,
• смешанный обход правого поддерева.

Например, при обходе дерева на рисунке 9.8 смешанным методом вершины обрабатываются в следующей последовательности: h, d, i, b, e, a, f, c, j, g.

1. Восходящий обход:

• восходящий обход левого поддерева,
• восходящий обход правого поддерева,
• обработка корня.

Порядок обработки вершин того же дерева при восходящем обходе выглядит так: h, i, d, e, b, f, j, g, c, a.

Для методов обхода в применении к бинарным деревьям часто применяют специфичные названия: нисходящий обход называют обходом pre‑order, смешанный обход  обходом in—order и восходящий  обходом post‑order. Обход post‑order чаще всего применяется для уничтожения всех вершин в бинарном дереве, когда процесс уничтожения можно было бы описать следующим образом: «чтобы уничтожить все вершины бинарного дерева, необходимо уничтожить левое поддерево корня, затем правое поддерево, а затем и сам корень».

Все три метода легко представить рекурсивными процедурами. Прежде чем это сделать, необходимо определить процедуру, активируемую на этапе «обработка». Такая процедура должна выполнять некоторые действия над вершиной, к которой получен доступ на текущем шаге просмотра. А доступ к элементу связной структуры легче всего обеспечить через указатель, который назовем pNode. Текст такой процедуры может выглядеть, например, следующим образом:

Procedure ProcessingNode(pNode: Pvertex);

Теперь можно привести тексты трех подпрограмм обхода, которые реализуют приведенные выше рекурсивные алгоритмы:

Procedure PreOrder(pRoot: Pvertex);

If (aRoot <> Nil) Then Begin

Procedure InOrder(pRoot: Pvertex);

If (aRoot <> Nil) Then Begin

Procedure PostOrder(pRoot: Pvertex);

If (aRoot <> Nil) Then Begin

Для активации любой из этих трех процедур, следует воспользоваться вызовом в следующем виде:

где Root  указатель корня, например: PostOrder(Root).

Преобразование любого дерева к бинарному дереву

Любое m-арное дерево (т. е. дерево степени m) может быть преобразовано в эквивалентное ему бинарное дерево, которое проще исходного дерева с точки зрения представления в памяти и обработки. Графически такое преобразование сводится к следующим действиям:

1. сначала в каждом узле исходного дерева вычеркиваем все ветви, кроме самой левой ветви, которая соответствует ссылке на старшего сына;
2. в получившемся графе соединяем те узлы одного уровня, которые являются братьями в исходном дереве.

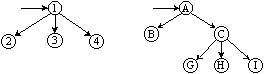
На рисунке 9.10 приведен пример такого преобразования, причем после него из некоторых элементов, исходят две ссылки: горизонтальная соединяет данный элемент с его младшим (в исходном дереве) братом, а вертикальная  с его старшим сыном. Если на рисунке 9.10 повернуть все ссылки на 45° по часовой стрелке, то получим структуру, очень похожую на двоичное дерево. Однако считать ее таковым было бы ошибкой, поскольку функционально горизонтальные и вертикальные ссылки на рисунке 9.10 б имеют совершенно разный смысл. Правильнее было бы использовать следующую интерпретацию: после выполнения указанных преобразований из сыновей каждого родителя образуется линейный список, причем на старшего сына указывает ссылка от его родителя, а сам старший сын находится в голове списка своих братьев.

Рисунок 9.10  Преобразование 3-арного дерева к бинарному

Пользуясь аналогичным алгоритмом можно представить в виде двоичного дерева и лес. На рисунке 9.11 показаны этапы преобразования леса из двух деревьев в бинарное дерево.

Переход от m-арного дерева (или леса) к представлению в виде двоичного дерева при естественном связном хранении сокращает объем занимаемой памяти, поскольку каждый элемент m-арного дерева должен иметь m полей для логических указателей, тогда как элемент двоичного дерева имеет только два таких поля. С другой стороны, при таком преобразовании нужно помнить о функциональном назначении левой и правой ссылок и учитывать это при обработке дерева.

Рисунок 9.11  Преобразование леса к бинарному дереву

Источник

80 25 17

Нетрудно заметить, что процесс конструирования такого дерева про­исходит сверху вниз, начиная с корня, путем последовательного сравнения числовых значений, размещаемых в вершинах, с целью определения места размещения соответствующей вершины в структуре дерева. Любая модификация дихотомического дерева (удаление вершины, вставка новой веpшины) не должна нарушать дихотомической структуры в целом.

В об­щем случае трансформация произвольной информационной строки (пос­ледо­ва­тель­ности объектов) в структуру дерева и об­рат­но основана на использовании глубоких структурных межобъектных отно­шений в исходной строке. Такая трансформация позволяет наг­ляд­­но представить подобные отношения в форме дерева. В программировании дерево во многом рассматривается как формальная структура, наполняемая различным семантическим содержанием. Такой под­ход позволяет формально реализовать многие преобразования дан­ных на основе унифицированных процедур обхода деревьев.

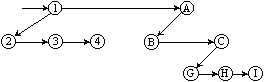
Нап­ри­мер, в теории трансляции широко используется понятие Поль­ской инверсной записи (ПОЛИЗ) – особой системы представления математических выражений символьными последовательностями. Так, например, выражение » a + b * c » будет представлено в ПОЛИЗЕ строкой » a b c * + «. Если представить исходное выражение в естественной иерархической форме бинарного дерева :

то его восходящий обход (пунктир на рис. 4) приведет к стро­ке » a b c * + «, определяющей «польский» эквивалент исходной стро­ки. Формула восходящего обхода «Левый–Правый–Корень» (ЛПК) определяет правило обхода бинарного дерева: восходящий об­ход связан с обходом его левого поддерева, затем правого под­де­ре­ва, затем корня. Поскольку каждая вершина дерева может интер­пре­­тироваться как корень «вырастающего из нее» поддерева, это пра­­вило применяется рекурсивно к каждой вершине обходимого де­ре­ва. Правило ЛКП (Левый–Корень–Правый) определяет так на­зы­ва­е­­мый смешанный обход, правило КЛП – нисходящий обход и т.д. Нет­ру­дно заметить, что смешанный обход дерева дихотомии по пра­вилу ЛКП приведет к формированию строки чисел (хранящихся в вершинах этого дерева), упорядоченной по возрастанию, а такой же обход по правилу ПКЛ – к формированию строки, упорядоченной по убыванию соответствующих чисел. Таким образом, между структурой дерева, от­ношением порядка на множестве информационных компонент его вер­шин и видом обхода существует глубокая связь, определяемая ре­­курсивной природой структуры дерева. Рекурсивные процедуры об­хо­да бинарных деревьев пишутся прямо по формуле обхода с учетом спе­цификации представления вершин дерева. Например, ниже при­ве­де­на процедура смешанного обхода бинарного дерева дихотомии, ре­а­лизующего формулу ЛКП.

TYPE Вершина = POINTER TO Элемент ;

PROCEDURE Смеш_Обход (K : Вершина);

Смеш_Обход (K^.LLink); (* Обход левого поддерева *)

WriteCard (K^.Info); (* Обработка корня *)

Смеш_Обход (K^.RLink); (* Обход правого поддерева *)

В традиционном программировании рекурсия часто рас­сма­три­ва­ет­ся как некоторый заменитель итерации. Причем в качестве примеров рас­сматривается вычисление рекуррентных последовательностей, ко­то­рые могут быть легко сформированы и обычными итераторами (цик­ла­ми WHILE, REPEAT и т.п.). Природа рекурсии значительно глубже, чем механизм итерации, поэтому ее использование практически не име­ет альтернатив в виде итераторов только тогда, когда решение за­дач проводится на рекурсивных структурах. Попробуйте написать про­цедуру Смеш-Обход без использования рекурсии, только на ос­но­ве циклов и, если Вам это удастся, сравните ее с приведенным вы­ше вариантом рекурсивной процедуры по наглядности, лаконичности, вы­разительности.

Источник

Операции над деревьями.

Над деревьями определены следующие основные операции:

• 1) Поиск узла с заданным ключом.
• 2) Добавление нового узла
• 3) Удаление узла ( поддерева ) .
• 4) Обход дерева в определенном порядке:
  • Нисходящий обход ;
  • Смешанный обход ;
  • Восходящий обход.

ПОИСК ЗАПИСИ В ДЕРЕВЕ Нужная вершина в дереве ищется по ключу. Поиск в бинарном дереве осуществляется следующим образом. Пусть построено некоторое дерево и требуется найти звено с ключом X. Сначала сравниваем с X ключ, находящийся в корне дерева. В случае равенства поиск закончен и нужно возвратить указатель на корень в качестве результата поиска. В противном случае переходим к рассмотрению вершины, которая находится слева внизу, если ключ X меньше только что рассмотренного, или справа внизу, если ключ X больше только что рассмотренного. Сравниваем ключ X с ключом, содержащимся в этой вершине, и т.д. Процесс завершается в одном из двух случаев:

• 1) найдена вершина, содержащая ключ, равный ключу X;
• 2) в дереве отсутствует вершина, к которой нужно перейти для выполнения очередного шага поиска.

В первом случае возвращается указатель на найденную вершину. Во втором — указатель на звено, где остановился поиск, (что удобно для построения дерева ). ДОБАВЛЕНИЕ НОВОГО УЗЛА Для включения записи в дерево прежде всего нужно найти в дереве ту вершину, к которой можно «подвести» (присоединить) новую вершину, соответствующую включаемой записи. При этом упорядоченность ключей должна сохраняться. Алгоритм поиска нужной вершины, вообще говоря, тот же самый, что и при поиске вершины с заданным ключом. Эта вершина будет найдена в тот момент, когда в качестве очередного указателя, определяющего ветвь дерева, в которой надо продолжить поиск, окажется указатель NIL ( случай 2 в поиске записи в дереве). ОБХОД ДЕРЕВА. Во многих задачах, связанных с деревьями, требуется осуществить систематический просмотр всех его узлов в определенном порядке. Такой просмотр называется прохождением или обходом дерева. Бинарное дерево можно обходить тремя основными способами: нисходящим, смешанным и восходящим ( возможны также обратный нисходящий, обратный смешанный и обратный восходящий обходы). Принятые выше названия методов обхода связаны с временем обработки корневой вершины: До того как обработаны оба ее поддерева, после того как обработано левое поддерево, но до того как обработано правое , после того как обработаны оба поддерева. Используемые в переводе названия методов отражают направление обхода в дереве: от корневой вершины вниз к листьям — нисходящий обход; от листьев вверх к корню — восходящий обход, и смешанный обход — от самого левого листа дерева через корень к самому правому листу. Схематично алгоритм обхода двоичного дерева в соответствии с нисходящим способом может выглядеть следующим образом:

• 1. В качестве очередной вершины взять корень дерева. Перейти к пункту 2.
• 2. Произвести обработку очередной вершины в соответствии с требованиями задачи. Перейти к пункту 3.
• 3.а) Если очередная вершина имеет обе ветви, то в качестве новой вершины выбрать ту вершину, на которую ссылается левая ветвь, а вершину, на которую ссылается правая ветвь, занести в стек; перейти к пункту 2;
• 3.б) если очередная вершина является конечной, то выбрать в качестве новой очередной вершины вершину из стека, если он не пуст, и перейти к пункту 2; если же стек пуст, то это означает, что обход всего дерева окончен, перейти к пункту 4;
• 3.в) если очередная вершина имеет только одну ветвь, то в качестве очередной вершины выбрать ту вершину, на которую эта ветвь указывает, перейти к пункту 2.
• 4. Конец алгоритма.

Для примера рассмотрим возможные варианты обхода дерева (рис. 4.1). При обходе дерева представленного на рис.1 этими тремя методами мы получим следующие последовательности: ABCDEFG ( нисходящий ); CBAFEDG ( смешанный ); CBFEGDA ( восходящий ). Рис.4.1. Схема дереваВОСХОДЯЩИЙ ОБХОД Трудность заключается в том, что в этом алгоритме каждая вершина запоминается в стеке дважды: первый раз — когда обходится левое поддерево, и второй раз — когда обходится правое поддерево. Таким образом, в алгоритме необходимо различать два вида стековых записей: 1-й означает, что в данный момент обходится левое поддерево; 2-й — что обходится правое, поэтому в стеке запоминается указатель на узел и признак (код-1 и код-2 соответственно). Алгоритм восходящего обхода можно представить следующим образом:

• 1) Спуститься по левой ветви с запоминанием вершины в стеке как 1-й вид стековых записей;
• 2) Если стек пуст, то перейти к п.5;
• 3) Выбрать вершину из стека, если это первый вид стековых записей, то возвратить его в стек как 2-й вид стековых записей; перейти к правому сыну; перейти к п.1, иначе перейти к п.4;
• 4) Обработать данные вершины и перейти к п.2;
• 5) Конец алгоритма.

Источник