Главная » Деревья

Сортировка красно черным деревом

Содержание
  1. Introduction to Red-Black Tree
  2. Properties of Red Black Tree:
  3. Rules That Every Red-Black Tree Follows:
  4. Why Red-Black Trees?
  5. Interesting points about Red-Black Tree:
  6. Black Height of a Red-Black Tree :
  7. Search Operation in Red-black Tree:
  8. Exercise:
  9. Insertion and Deletion
  10. Applications:
  11. Advantages:
  12. Disadvantages:
  13. References:
  14. Красно-черные деревья: коротко и ясно
  15. Как бинарное дерево, красно-черное обладает свойствами:
  16. ключи всех левых потомков (в других определениях дубликаты должны располагаться с правой стороны либо вообще отсутствовать). Это неравенство должно быть истинным для всех потомков узла, а не только его дочерних узлов. Свойства красно-черных деревьев: 1) Каждый узел окрашен либо в красный, либо в черный цвет (в структуре данных узла появляется дополнительное поле – бит цвета). 2) Корень окрашен в черный цвет. 3) Листья(так называемые NULL-узлы) окрашены в черный цвет. 4) Каждый красный узел должен иметь два черных дочерних узла. Нужно отметить, что у черного узла могут быть черные дочерние узлы. Красные узлы в качестве дочерних могут иметь только черные. 5) Пути от узла к его листьям должны содержать одинаковое количество черных узлов(это черная высота). Ну и почему такое дерево является сбалансированным? Действительно, красно-черные деревья не гарантируют строгой сбалансированности (разница высот двух поддеревьев любого узла не должна превышать 1), как в АВЛ-деревьях. Но соблюдение свойств красно-черного дерева позволяет обеспечить выполнение операций вставки, удаления и выборки за время . И сейчас посмотрим, действительно ли это так. Пусть у нас есть красно-черное дерево. Черная высота равна (black height). Если путь от корневого узла до листового содержит минимальное количество красных узлов (т.е. ноль), значит этот путь равен . Если же путь содержит максимальное количество красных узлов ( в соответствии со свойством ), то этот путь будет равен . То есть, пути из корня к листьям могут различаться не более, чем вдвое (, где h — высота поддерева), этого достаточно, чтобы время выполнения операций в таком дереве было Как производится вставка? Вставка в красно-черное дерево начинается со вставки элемента, как в обычном бинарном дереве поиска. Только здесь элементы вставляются в позиции NULL-листьев. Вставленный узел всегда окрашивается в красный цвет. Далее идет процедура проверки сохранения свойств красно-черного дерева . Свойство 1 не нарушается, поскольку новому узлу сразу присваивается красный цвет. Свойство 2 нарушается только в том случае, если у нас было пустое дерево и первый вставленный узел (он же корень) окрашен в красный цвет. Здесь достаточно просто перекрасить корень в черный цвет. Свойство 3 также не нарушается, поскольку при добавлении узла он получает черные листовые NULL-узлы. В основном встречаются 2 других нарушения: 1) Красный узел имеет красный дочерний узел (нарушено свойство ). 2) Пути в дереве содержат разное количество черных узлов (нарушено свойство ). Подробнее о балансировке красно-черного дерева при разных случаях (их пять, если включить нарушение свойства ) можно почитать на wiki. Это вообще где-то используется? Да! Когда в институте на третьем курсе нам читали «Алгоритмы и структуры данных», я и не могла представить, что красно-черные деревья где-то используются. Помню, как мы не любили тему сбалансированных деревьев. Ох уж эти родственные связи в красно-черных деревьях («дядя», «дедушка», «чёрный брат и крестный красный отец»), прям Санта-Барбара какая-то. Правые и левые, малые и большие повороты АВЛ-деревьев – сплошные американские горки. Вы тоже не любите красно-черные деревья? Значит, просто не умеете их готовить. А кто-то просто взял и приготовил. Так, например, ассоциативные массивы в большинстве библиотек реализованы именно через красно-черные деревья. Это все, что я хотела рассказать. Источник
  17. Свойства красно-черных деревьев:
  18. Ну и почему такое дерево является сбалансированным?
  19. Как производится вставка?
  20. Это вообще где-то используется?

Introduction to Red-Black Tree

When it comes to searching and sorting data, one of the most fundamental data structures is the binary search tree. However, the performance of a binary search tree is highly dependent on its shape, and in the worst case, it can degenerate into a linear structure with a time complexity of O(n). This is where Red Black Trees come in, they are a type of balanced binary search tree that use a specific set of rules to ensure that the tree is always balanced. This balance guarantees that the time complexity for operations such as insertion, deletion, and searching is always O(log n), regardless of the initial shape of the tree.

Читайте также:  Дерево целей промышленного предприятия

Red Black Trees are self-balancing, meaning that the tree adjusts itself automatically after each insertion or deletion operation. It uses a simple but powerful mechanism to maintain balance, by coloring each node in the tree either red or black.

Red Black Tree-

Red-Black tree is a binary search tree in which every node is colored with either red or black. It is a type of self balancing binary search tree. It has a good efficient worst case running time complexity.

Properties of Red Black Tree:

The Red-Black tree satisfies all the properties of binary search tree in addition to that it satisfies following additional properties –

1. Root property: The root is black.

2. External property: Every leaf (Leaf is a NULL child of a node) is black in Red-Black tree.

3. Internal property: The children of a red node are black. Hence possible parent of red node is a black node.

4. Depth property: All the leaves have the same black depth.

5. Path property: Every simple path from root to descendant leaf node contains same number of black nodes.

The result of all these above-mentioned properties is that the Red-Black tree is roughly balanced.

Rules That Every Red-Black Tree Follows:

  1. Every node has a color either red or black.
  2. The root of the tree is always black.
  3. There are no two adjacent red nodes (A red node cannot have a red parent or red child).
  4. Every path from a node (including root) to any of its descendants NULL nodes has the same number of black nodes.
  5. Every leaf (e.i. NULL node) must be colored BLACK.

Why Red-Black Trees?

Most of the BST operations (e.g., search, max, min, insert, delete.. etc) take O(h) time where h is the height of the BST. The cost of these operations may become O(n) for a skewed Binary tree. If we make sure that the height of the tree remains O(log n) after every insertion and deletion, then we can guarantee an upper bound of O(log n) for all these operations. The height of a Red-Black tree is always O(log n) where n is the number of nodes in the tree.

Sr. No. Algorithm Time Complexity
1. Search O(log n)
2. Insert O(log n)
3. Delete O(log n)

“n” is the total number of elements in the red-black tree.

Comparison with AVL Tree:
The AVL trees are more balanced compared to Red-Black Trees, but they may cause more rotations during insertion and deletion. So if your application involves frequent insertions and deletions, then Red-Black trees should be preferred. And if the insertions and deletions are less frequent and search is a more frequent operation, then AVL tree should be preferred over the Red-Black Tree.

How does a Red-Black Tree ensure balance?
A simple example to understand balancing is, that a chain of 3 nodes is not possible in the Red-Black tree. We can try any combination of colors and see if all of them violate the Red-Black tree property.

Proper structure of three noded Red-black tree

Interesting points about Red-Black Tree:

  1. The black height of the red-black tree is the number of black nodes on a path from the root node to a leaf node. Leaf nodes are also counted as black nodes. So, a red-black tree of height h has black height >= h/2.
  2. Height of a red-black tree with n nodes is h2(n + 1).
  3. All leaves (NIL) are black.
  4. The black depth of a node is defined as the number of black nodes from the root to that node i.e the number of black ancestors.
  5. Every red-black tree is a special case of a binary tree.

Black Height of a Red-Black Tree :

Black height is the number of black nodes on a path from the root to a leaf. Leaf nodes are also counted black nodes. From the above properties 3 and 4, we can derive, a Red-Black Tree of height h has black-height >= h/2.

Number of nodes from a node to its farthest descendant leaf is no more than twice as the number of nodes to the nearest descendant leaf.

Every Red Black Tree with n nodes has height 2Log2(n+1)
This can be proved using the following facts:

  1. For a general Binary Tree, let k be the minimum number of nodes on all root to NULL paths, then n >= 2 k – 1 (Ex. If k is 3, then n is at least 7). This expression can also be written as k 2(n+1).
  2. From property 4 of Red-Black trees and above claim, we can say in a Red-Black Tree with n nodes, there is a root to leaf path with at-most Log2(n+1) black nodes.
  3. From properties 3 and 5 of Red-Black trees, we can claim that the number of black nodes in a Red-Black tree is at least ⌊ n/2 ⌋ where n is the total number of nodes.
Читайте также:  Чем отличается цветок от дерева

From the above points, we can conclude the fact that Red Black Tree with n nodes has a height 2(n+1)

Search Operation in Red-black Tree:

As every red-black tree is a special case of a binary tree so the searching algorithm of a red-black tree is similar to that of a binary tree.

searchElement (tree, val) Step 1: If tree -> data = val OR tree = NULL Return tree Else If val < data Return searchElement (tree ->left, val) Else Return searchElement (tree -> right, val) [ End of if ] [ End of if ] Step 2: END

For the program, you can refer it for AVL tree.

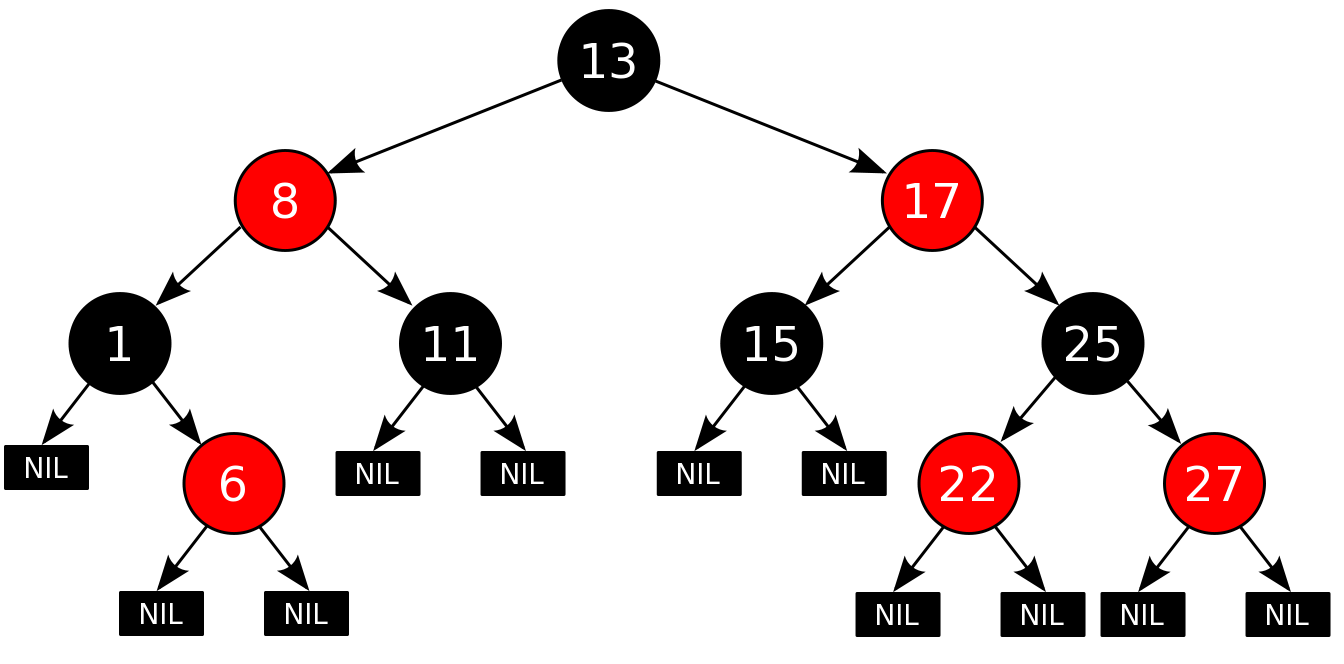
Example: Searching 11 in the following red-black tree.

  1. Start from the root.
  2. Compare the inserting element with root, if less than root, then recurse for left, else recurse for right.
  3. If the element to search is found anywhere, return true, else return false.

Just follow the blue bubble.

In this post, we introduced Red-Black trees and discussed how balance is ensured. The hard part is to maintain balance when keys are added and removed. We have also seen how to search an element from the red-black tree. We will soon be discussing insertion and deletion operations in coming posts on the Red-Black tree.

Exercise:

1) Is it possible to have all black nodes in a Red-Black tree?
2) Draw a Red-Black Tree that is not an AVL tree structure-wise?

Insertion and Deletion

Applications:

  1. Most of the self-balancing BST library functions like map, multiset, and multimap in C++ ( or java packages like java.util.TreeMap and java.util.TreeSet ) use Red-Black Trees.
  2. It is used to implement CPU Scheduling Linux. Completely Fair Scheduler uses it.
  3. It is also used in the K-mean clustering algorithm in machine learning for reducing time complexity.
  4. Moreover, MySQL also uses the Red-Black tree for indexes on tables in order to reduce the searching and insertion time.
  5. Red Black Trees are used in the implementation of the virtual memory manager in some operating systems, to keep track of memory pages and their usage.
  6. Many programming languages such as Java, C++, and Python have implemented Red Black Trees as a built-in data structure for efficient searching and sorting of data.
  7. Red Black Trees are used in the implementation of graph algorithms such as Dijkstra’s shortest path algorithm and Prim’s minimum spanning tree algorithm.
  8. Red Black Trees are used in the implementation of game engines.

Advantages:

  1. Red Black Trees have a guaranteed time complexity of O(log n) for basic operations like insertion, deletion, and searching.
  2. Red Black Trees are self-balancing.
  3. Red Black Trees can be used in a wide range of applications due to their efficient performance and versatility.
  4. The mechanism used to maintain balance in Red Black Trees is relatively simple and easy to understand.
Читайте также:  Высокие быстрорастущие хвойные деревья

Disadvantages:

  1. Red Black Trees require one extra bit of storage for each node to store the color of the node (red or black).
  2. Complexity of Implementation.
  3. Although Red Black Trees provide efficient performance for basic operations, they may not be the best choice for certain types of data or specific use cases.

References:

Similar read thumbnail

Like Article

Источник

Красно-черные деревья: коротко и ясно

Итак, сегодня хочу немного рассказать о красно-черных деревьях. Рассказ будет кратким, без рассмотрения алгоритмов балансировки при вставке/удалении элементов в красно-черных деревьях.

Красно-черные деревья относятся к сбалансированным бинарным деревьям поиска.

Как бинарное дерево, красно-черное обладает свойствами:

1) Оба поддерева являются бинарными деревьями поиска.

2) Для каждого узла с ключом выполняется критерий упорядочения:

ключи всех левых потомков

(в других определениях дубликаты должны располагаться с правой стороны либо вообще отсутствовать).
Это неравенство должно быть истинным для всех потомков узла, а не только его дочерних узлов.

Свойства красно-черных деревьев:

1) Каждый узел окрашен либо в красный, либо в черный цвет (в структуре данных узла появляется дополнительное поле – бит цвета).

2) Корень окрашен в черный цвет.

3) Листья(так называемые NULL-узлы) окрашены в черный цвет.

4) Каждый красный узел должен иметь два черных дочерних узла. Нужно отметить, что у черного узла могут быть черные дочерние узлы. Красные узлы в качестве дочерних могут иметь только черные.

5) Пути от узла к его листьям должны содержать одинаковое количество черных узлов(это черная высота).

Ну и почему такое дерево является сбалансированным?

Действительно, красно-черные деревья не гарантируют строгой сбалансированности (разница высот двух поддеревьев любого узла не должна превышать 1), как в АВЛ-деревьях. Но соблюдение свойств красно-черного дерева позволяет обеспечить выполнение операций вставки, удаления и выборки за время . И сейчас посмотрим, действительно ли это так.

Пусть у нас есть красно-черное дерево. Черная высота равна (black height).

Если путь от корневого узла до листового содержит минимальное количество красных узлов (т.е. ноль), значит этот путь равен .

Если же путь содержит максимальное количество красных узлов ( в соответствии со свойством ), то этот путь будет равен .

То есть, пути из корня к листьям могут различаться не более, чем вдвое (, где h — высота поддерева), этого достаточно, чтобы время выполнения операций в таком дереве было

Как производится вставка?

Вставка в красно-черное дерево начинается со вставки элемента, как в обычном бинарном дереве поиска. Только здесь элементы вставляются в позиции NULL-листьев. Вставленный узел всегда окрашивается в красный цвет. Далее идет процедура проверки сохранения свойств красно-черного дерева .

Свойство 1 не нарушается, поскольку новому узлу сразу присваивается красный цвет.

Свойство 2 нарушается только в том случае, если у нас было пустое дерево и первый вставленный узел (он же корень) окрашен в красный цвет. Здесь достаточно просто перекрасить корень в черный цвет.

Свойство 3 также не нарушается, поскольку при добавлении узла он получает черные листовые NULL-узлы.

В основном встречаются 2 других нарушения:

1) Красный узел имеет красный дочерний узел (нарушено свойство ).

2) Пути в дереве содержат разное количество черных узлов (нарушено свойство ).

Подробнее о балансировке красно-черного дерева при разных случаях (их пять, если включить нарушение свойства ) можно почитать на wiki.

Это вообще где-то используется?

Да! Когда в институте на третьем курсе нам читали «Алгоритмы и структуры данных», я и не могла представить, что красно-черные деревья где-то используются. Помню, как мы не любили тему сбалансированных деревьев. Ох уж эти родственные связи в красно-черных деревьях («дядя», «дедушка», «чёрный брат и крестный красный отец»), прям Санта-Барбара какая-то. Правые и левые, малые и большие повороты АВЛ-деревьев – сплошные американские горки. Вы тоже не любите красно-черные деревья? Значит, просто не умеете их готовить. А кто-то просто взял и приготовил. Так, например, ассоциативные массивы в большинстве библиотек реализованы именно через красно-черные деревья.

Это все, что я хотела рассказать.

Источник

Оцените статью
© 2024 Деревья и растения