2.5.2.5. Древесная сортировка
При использовании этой сортировки в массиве постоянно поддерживается такой порядок, при котором максимальный элемент всегда будет оказываться в A[1]. Сортировка называется древесной, потому что в этом методе используется структура данных, называемая двоичным деревом. При чем используется представление дерева в виде массива (см. п. 1.3.4.4) и при сортировке используется тот же способ расположения вершин дерева в массиве.
Пусть A[1]. A[n] – массив, подлежащий сортировке. Вершинами дерева будут числа от 1 до n; о числе A[i] будем говорить как о числе, стоящем в вершине i. В процессе сортировки количество вершин дерева будет сокращаться. Число вершин текущего дерева будем хранить в переменной k. Таким образом, в процессе работы алгоритма массив A[1]. A[n] делится на две части: в A[1]. A[k] хранятся числа на дереве, а в A[k+1]. A[n] хранится уже отсортированная в порядке возрастания часть массива – элементы, уже занявшие свое законное место (рис. 44).
На каждом шаге алгоритм будет изымать максимальный элемент дерева, и помещать его в отсортированную часть, на освободившееся в результате сокращения дерева место.
Договоримся о терминологии. Вершинами дерева считаются числа от 1 до текущего значения переменной k. У каждой вершины s могут быть потомки 2s и 2s + 1. Если оба этих числа больше k, то потомков нет; такая вершина называется листом. Если 2s = k, то вершина s имеет ровно одного потомка (2s).
Для каждого s из 1. k рассмотрим «поддерево» с корнем в s: оно содержит вершину s и всех ее потомков. Вершина s называется р е г у -л я р н о й , если стоящее в ней число – максимальный элемент s-поддерева; s-поддерево называется регулярным, если все его вершины регу-137
лярны. В частности, любой лист образует регулярное одноэлементное поддерево.
Теперь запишем алгоритм сортировки:
procedure TreeSort (n: integer;
u, k: integer; procedure Exchange(i, j: integer); var
procedure Restore(s: integer);
Источник
Сортировка с помощью дерева
Сортировка с помощью дерева осуществляется на основе бинарного дерева поиска.
Бинарное (двоичное) дерево поиска – это бинарное дерево, для которого выполняются следующие дополнительные условия (свойства дерева поиска):
- оба поддерева – левое и правое, являются двоичными деревьями поиска;
- у всех узлов левого поддерева произвольного узла X значения ключей данных меньше, чем значение ключа данных самого узла X;
- у всех узлов правого поддерева произвольного узла X значения ключей данных не меньше, чем значение ключа данных узла X.
Данные в каждом узле должны обладать ключами, на которых определена операция сравнения меньше.
Для сортировки с помощью дерева исходная сортируемая последовательность представляется в виде структуры данных «дерево».
Например, исходная последовательность имеет вид:
4, 3, 5, 1, 7, 8, 6, 2
Корнем дерева будет начальный элемент последовательности. Далее все элементы, меньшие корневого, располагаются в левом поддереве, все элементы, большие корневого, располагаются в правом поддереве. Причем это правило должно соблюдаться на каждом уровне.
После того, как все элементы размещены в структуре «дерево», необходимо вывести их, используя инфиксную форму обхода.
Реализация сортировки с помощью дерева на C++
#include
using namespace std;
// Структура — узел дерева
struct tnode
int field; // поле данных
struct tnode *left; // левый потомок
struct tnode *right; // правый потомок
>;
// Вывод узлов дерева (обход в инфиксной форме)
void treeprint(tnode *tree)
if (tree != NULL ) < //Пока не встретится пустой узел
treeprint(tree->left); //Рекурсивная функция вывода левого поддерева
cout field treeprint(tree->right); //Рекурсивная функция вывода правого поддерева
>
>
// Добавление узлов в дерево
struct tnode * addnode( int x, tnode *tree) if (tree == NULL ) // Если дерева нет, то формируем корень
tree = new tnode; //память под узел
tree->field = x; //поле данных
tree->left = NULL ;
tree->right = NULL ; //ветви инициализируем пустотой
>
else // иначе
if (x < tree->field) //Если элемент x меньше корневого, уходим влево
tree->left = addnode(x, tree->left); //Рекурсивно добавляем элемент
else //иначе уходим вправо
tree->right = addnode(x, tree->right); //Рекурсивно добавляем элемент
return (tree);
>
//Освобождение памяти дерева
void freemem(tnode *tree)
if (tree != NULL ) // если дерево не пустое
freemem(tree->left); // рекурсивно удаляем левую ветку
freemem(tree->right); // рекурсивно удаляем правую ветку
delete tree; // удаляем корень
>
>
// Тестирование работы
int main()
struct tnode *root = 0; // Объявляем структуру дерева
system( «chcp 1251» ); // переходим на русский язык в консоли
system( «cls» );
int a; // текущее значение узла
// В цикле вводим 8 узлов дерева
for ( int i = 0; i < 8; i++)
cout cin >> a;
root = addnode(a, root); // размещаем введенный узел на дереве
>
treeprint(root); // выводим элементы дерева, получаем отсортированный массив
freemem(root); // удаляем выделенную память
cin.get(); cin.get();
return 0;
>
Результат выполнения
Комментариев к записи: 3
Источник
Сортировка декартовым деревом
Суть алгоритма в том, что на основании массива строится так называемое декартово дерево. А из построенного декартового дерева очень легко получить все элементы в порядке возрастания или убывания.
Компания EDISON всегда рада приобщиться к прекрасному.
Один из наших классических проектов — диагностика хранилища документов Vivaldi, благодаря чему оптимизирован одновременный доступ к тысячам документам и произведениям в сетевой библиотеке.
Мы очень любим сеять разумное, доброе, вечное! 😉
В рамках этой статьи я решил воздержаться от подробной теории и не стану разъяснять, что такое декартово дерево, как его построить и какие с ним возможны операции. Это уже прекрасно сделано и до меня — на Хабре есть превосходный материал, где все эти моменты удачно и подробно освещены — в конце этой лекции есть раздел «Ссылки», где можно перейти к этим хабрастатьям. В дальнейшем я буду освещать некоторые моменты, характерные для этой структуры, но при этом подразумевается, что вы понимаете её специфику или, в случае заинтересованности, готовы её изучить по указанным ниже ссылкам.
Декартово дерево является гибридной структурой, объединяющей в себе свойства кучи и бинарного дерева поиска. Для этого дерева есть синонимы, которые будут использоваться в статье:
дерамида (дерево + пирамида),
трип (treap — tree + heap)
и даже дуча (дерево + куча).
Давайте возьмём для примера вот этот массив:
и последовательно взглянем, как для него выглядит двоичное дерево поиска, куча и дерамида.
Бинарное дерево поиска


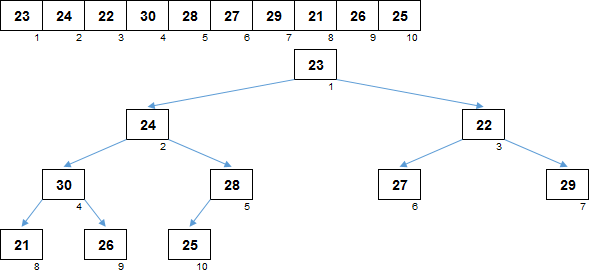
Внешний вид дерева сильно зависит от того, как изначально расположены элементы массива. На рандомных данных, дерево с высокой долей вероятности получится несбалансирвоанным, с гораздо большим количеством уровней, по сравнению с оптимальным. В нашем примере образовалось 7 уровней. Если бы элементы массива располагались, например, в таком порядке:
25, 28, 29, 23, 30, 27, 24, 22, 21, 26
дерево поиска бы получилось сбалансированным, с минимально возможным количеством уровней (= 4). Сортировка с помощью сбалансированного дерева имела бы сложность по времени: . Но в случае несбалансированного дерева может деградировать и до .
В предыдущей хабрастатье рассмотрена сортировка бинарным деревом поиска, а также её интересная модификация, позволяющая гарантировано сортировать с временно́й сложностью .
Чем более несбалансированным будет дерево поиска, тем более затратным будет его обход.
С другой стороны, хранение данных в дереве поиска весьма удобно с организационной точки зрения, позволяет с этими данными делать очень многие операции, сортировать в том числе.
Родитель в двоичном дереве поиска необязательно больше чем потомок. Но при этом левый потомок всегда меньше родителя, правый потомок всегда больше родителя (или равен ему).
Максимальный элемент массива при построении дерева поиска попадает где-то в правое поддерево. Чтобы этот максимум извлечь, дерево поиска надо полностью обойти.
Бинарная куча
В обычной куче очень просто организованы взаимосвязи «родитель — потомок», они привязаны к самим индексам элементов.
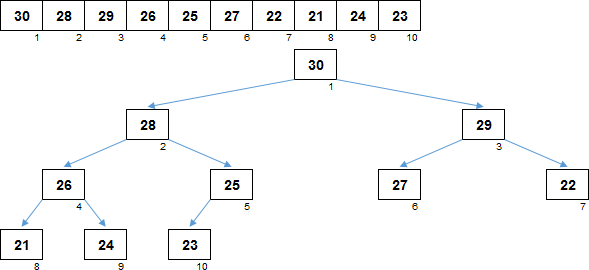
На рисунке на самом деле пока ещё не куча, поскольку такое дерево, изначально построенное на рандомном массиве ещё не является сортирующим. Нужно обойти каждый элемент и сделать для него просейку. В результате элементы в массиве перестроятся так, что каждый родитель будет больше своего потомка:
Максимальный элемент находится в корне дерева. Его расположение известно, его искать не нужно. С другой стороны, при если извлечь максимум из кучи (и вместо него в корень дерева приходится ставить какой-то другой элемент массива), куча перестаёт быть сортирующим деревом, её нужно опять просеивать.
Декартово дерево
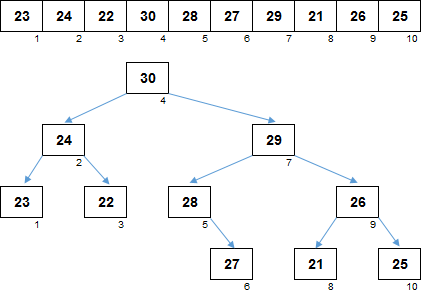
И, наконец, декартово дерево. Взаимосвязи установлены таким образом, что с одной стороны, оно является кучей, если смотреть на значения элементов. Все родители больше своих потомков:
С другой стороны, структура является бинарным деревом поиска, если смотреть на индексы элементов. На изображении в дереве для наглядности убрали в узлах значения элементов, оставили только индексы. Каждый левый потомок меньше родителя, каждый правый потомок — больше родителя:
С одной стороны, мы имеем быстрый доступ к максимальному элементу. Так как это куча, то максимум находится в корне.
С другой стороны, из структуры легко можно удалить максимум и работать с оставшимися данными дальше. Так как это бинарное дерево поиска, удаление корня не связано с большими затратами. Во взаимосвязях «родители-потомки» происходят относительно небольшие изменения, в корень декартова дерева попадает новый максимум и можно работать дальше.
Каждый элемент характеризуется двумя числами — значением элемента и индексом элемента в массиве. Индекс можно считать за координату X, значение — за Y, а сам элемент интепретировать как точку на координатной плоскости. Если родителей и потомков соединить стрелками, то получается примерно такая картина:
Фигура на графике полностью изоморфна декартову дереву чуть выше.
Сортировка декартовым деревом :: Cartesian tree sort
- I. На основании неотсортированного массива строим декартово дерево:
- I.1. Перебираем элементы массива слева-направо.
- I.1. Если это первый элемент массива, то он просто является самым первым узлом декартова дерева.
- I.2. Если это не первый элемент массива, считаем что это декартово дерево, состоящее из одного элемента. Производим операцию Merge этого дерева с тем деревом, которое построено из предыдущих элементов.
- II.1. Текущий максимальный элемент — корень дерева.
- II.2. Удаляем из дерева корень, сам максимальный элемент переносим в дополнительный массив.
- II.3. После удаления корня структура распалось на два декартова дерева.
- II.4. Для этих двух деревьев производим операцию Merge. Новым текущим максимумом становится один из корней объединяемых деревьев.
- II.5. Для нового максимума снова повторяем действия II.1-II.4.
Сложность
Декартово дерево с минимальными затратами обрабатывает отсортированные и почти отсортированные (причём неважно, по возрастанию или убыванию) участки массива. Вот, например, так выглядит процесс для реверсно упорядоченного массива:
Самая затратная часть алгоритма — это операция Merge, которую для каждого из n элементов приходится делать дважды — сначала при построении дерамиды и затем при её разборке. На рандомных данных однократная операция Merge обходится в , но для элементов, находящихся в упорядоченных областях массива стоимость операции O(1).
Таким образом, средняя и худшая временна́я сложность сортировки — , лучшая — O(n).
По дополнительной памяти дела обстоят похуже — O(n). Если бы декартово дерево было просто разновидностью кучи, то затраты были бы O(1). Но cartesian tree — это также и дерево бинарного поиска, из-за чего для всех n элементов приходится отдельно хранить взаимосвязи «родители-потомки».
Кроме того, реализация именно в таком виде означает, что это внешняя сортировка — отсортированные элементы собираются в отдельном массив. А это ещё O(n) по дополнительной памяти.
Ссылки
Cartesian
Декартово дерево: Часть 1, Часть 2, Часть 3
Статьи серии:
- Excel-приложение AlgoLab.xlsm
- Сортировки обменами
- Сортировки вставками
- Сортировки выбором
- Сортировки кучей: n-нарные пирамиды
- Сортировки кучей: числа Леонардо
- Сортировки кучей: слабая куча
- Сортировки кучей: декартово дерево
- Сортировки кучей: турнирное дерево
- Сортировки кучей: восходящая просейка
Источник