Сортировка выбором из дерева

Глава III Сортировка данных

Задача сортировки формулируется следующим образом: дана последовательность из n элементов a₁. a_n, выбранных из мно­жества, на котором задано отношение линейного порядка. Требу­ется найти перестановку s = (s(l),…,s(n)) индексов, для которой a_s(1) ≤ a_s(2) ≤ . ≤ a_s(n), т.е. расположить элементы данной последо­вательности в неубывающем порядке (или в невозрастающем, т.е. a_s(1) ≥ a_s(2) ≥ . ≥ a_s(n)).

Сортировка — практически важная и теоретически интересная задача. Она является неотъемлемой частью многих алгоритмов решения задач дискретной оптимизации. Решая задачу сортиров­ки, мы введем полезную структуру данных — представление массива в виде двоичного дерева данных. Такая структура пред­ставляет самостоятельный интерес и часто используется на прак­тике.

§1. Сложность задачи сортировки

Рассмотрим задачу сортировки в общем виде, когда информа­цию о последовательности элементов можно получать только с помощью операции сравнения двух элементов. Пусть а₁. а_n — последовательность сортируемых элементов. Не ограничивая общности, можно считать, что элементы заданной последовательности помещены в некоторый массив А в том же порядке, m есть A[i] = a, (i = 1,2. n).

Начнем с простейшего алгоритма сортировки данных, называемого алгоритмом сортировки выбором. Формализованное описание этого алгоритма представлено ниже.

АЛГОРИТМ 3.1. СОРТИРОВКА ВЫБОРОМ

Результат: массив А[1..n] такой, что А[1] ≤ А[2] ≤ . ≤ A[n].

1. begin
2. procedure MIN(i):
3. begin for j = i to n do
4. if A[i] < A[j] then A[i]↔A[j];
5. end;
6. begin (*главная программа*)
7. for i := 1 to n-1 do MIN(i);
8. end;
9. end.

Алгоритм 3.1 имеет следующую структуру. Процедура MIN(i) выбирает минимальный элемент из массива а_i. а_n и ставит его на первое место, т.е. на место a_i. Алгоритм начинает работу с вы­зова процедуры MIN(l), которая перемещает на первое место наименьший элемент исходного массива. Далее процедура по­вторяется для массива а₂. а_n и т.д. Теорема 3.1. Алгоритм СОРТИРОВКА ВЫБОРОМ имеет вы­числительную сложность O(n 2 ). □ Действительно, в процедуре MIN(i) осуществляется (n-i) операции сравнения и, в худшем случае, (n-i) операции обмена. Значит, общее число шагов, выполняемое процедурой MIN(i) пропорционально (n-i). Отсюда, число шагов алгоритма пропор­ционально (n — 1) + (n — 2) + . + 1 = n(n — 1 )/2, то есть сложность алгоритма есть O(n 2 ). Легко видеть, что число сравнений в алгоритме СОРТИРОВ­КА ВЫБОРОМ в точности равно n(n — 1)/2 , т.е. имеет порядок n2, как и сложность всего алгоритма. Ситуация эта не случайна, так как мы рассматриваем задачу сортировки в предположении, что информацию об элементах можно получать только с помо­щью операций сравнения. Поэтому в дальнейшем, оценивая сложность того или иного алгоритма, будем учитывать только операции сравнения, поскольку именно они и определяют слож­ность алгоритма. Следующая теорема дает оценку снизу сложности любого ал­горитма сортировки. Теорема 3.2. В любом алгоритме, упорядочивающем с помо­щью сравнений, на упорядочение последовательности из n эле­ментов тратится не менее c∙n∙loqn сравнений при некотором с > 0 и достаточно большом n. Любой алгоритм, упорядочивающий с помощью сравнений, можно схематично представить в виде корневого дерева (см. па­раграф 2.1.), называемого двоичным деревом решений. Это дере­во можно рассматривать как блок-схему алгоритма сортировки, в котором показаны все сравнения элементов и исходы алгоритма. Вершины дерева (кроме листьев) соответствуют сравнениям эле­ментов, при этом корень дерева соответствует первому сравне­нию, осуществляемому алгоритмом. Сыновья вершин изобража­ют возможные исходы сравнения отца. Листья соответствуют исходу алгоритма. На рис 3.1 изображено дерево решений алгоритма СОРТИ­РОВКИ ВЫБОРОМ для сортировки последовательности из трех элементов а₁,а₂,а₃. Здесь запись а:b означает сравнение элементов а и b. После сравнения а и b идем по левой дуге при а ≤ b и по правой при а ≥ b. Вообще говоря, исходом работы алгоритма явится последова­тельность из трех элементов такая, что а₁ ≤ а₂ ≤ а₃, однако окон­чательное значение а₁ может (за счет операции переприсваивания) отличаться от исходного. На рис. 3.1 листья изображают возможные исходы относительно начальных значений перемен­ных. 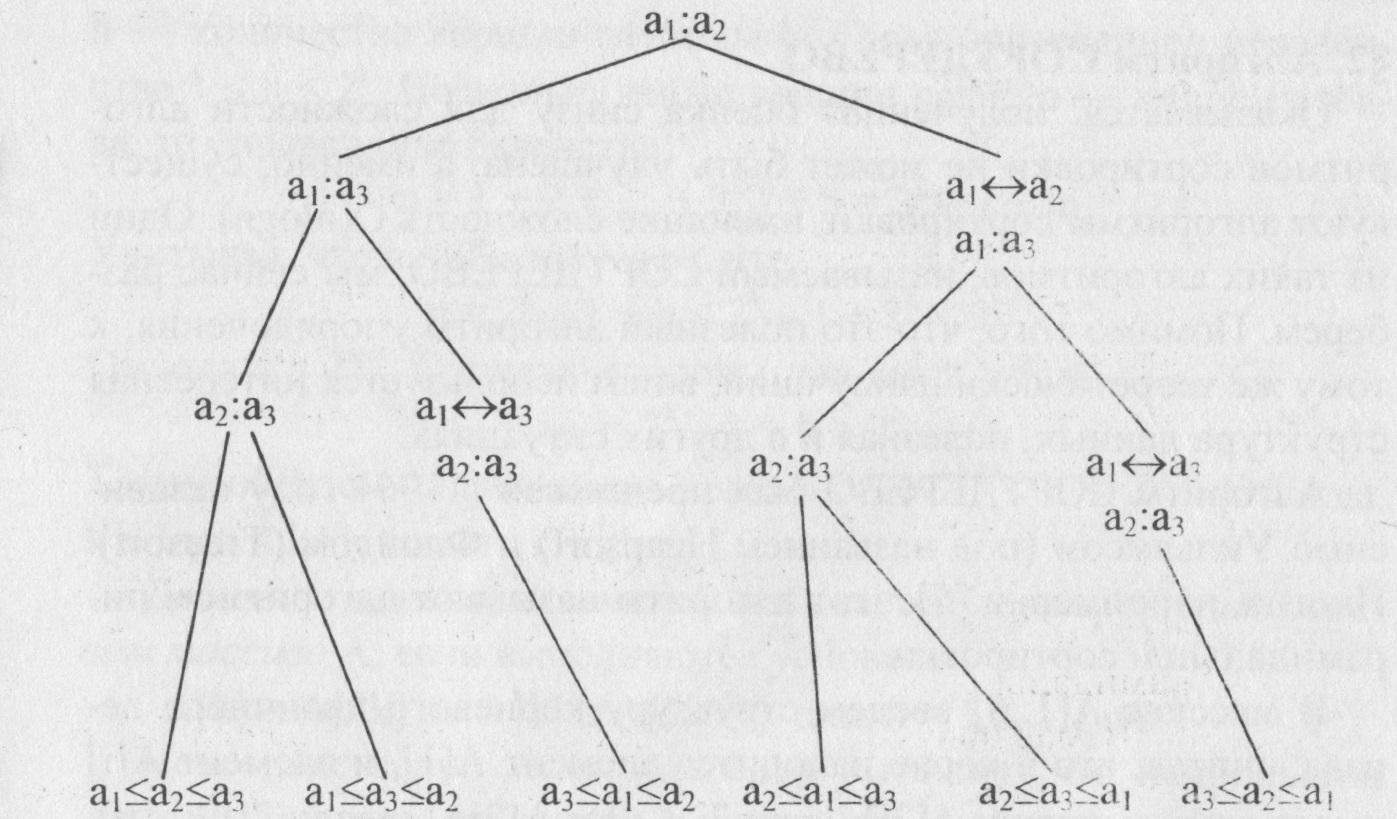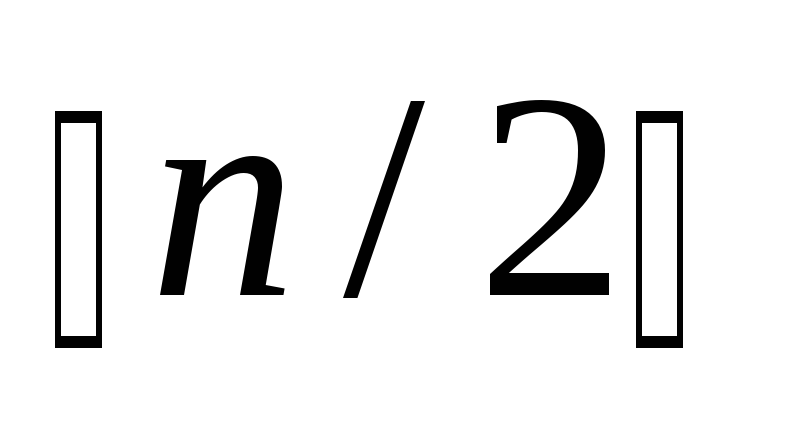Рис. 3.1. Двоичное дерево решений для сортировки трех элементов В любом таком дереве решений каждая перестановка опреде­ляет единственный путь от корня к листу. Поскольку алгоритм сортировки должен различать все возможные перестановки, по­лучаем, что дерево решений должно содержать как минимум n! листьев. При каждом входе алгоритм проходит весь путь от корня до листа, соответствующего данному входу. Следовательно, число операций сравнения, осуществляемое алгоритмом, равно длине пути от корня до листа, то есть равно высоте двоичного дерева решений. Таким образом, высота этого дерева дает оценку снизу сложности алгоритма. Поскольку, всякое двоичное дерево высоты к имеет не более 2 к листьев (лемма 2.1), то получаем, что должно выполняться не­равенство 2 к > n!, так как листьев в двоичном дереве решений должно быть не меньше, чем перестановок из n элементов. От­сюда, k > logn!. Осталось заметить, что при n > 1 справедлива следующая цепочка неравенств: n! ≥ n(n — 1 )(n — 2). () ≥ (n/2) n /2 , так что log n! ≥ log( n/2 ) n/2 = n/2 log n/2 ≥ n/4 log n Итак, k ≥ n/4 logn — полученное неравенство завершает дока­зательство теоремы 3.2.

Источник

Русские Блоги

Алгоритм сортировки-выбор (простой выбор, выбор дерева, сортировка кучи)

Основная идея выбора сортировки класса заключается в выборе записи с наименьшим ключевым словом среди записей n-i + 1 (i = 1,2, . n-1) в качестве i-й записи в упорядоченной последовательности. Основываясь на введении простой сортировки выбора, в этой статье представлены улучшенные алгоритмы сортировки по дереву и кучи.

1. Простой выбор сортировки

Идея алгоритма: В первом раунде простого выбора и сортировки, начиная с первой записи, путем сравнения ключевых слов N-1, запись с наименьшим ключевым словом выбирается из n записей и обменивается с первой записью. Во втором раунде простого выбора и сортировки, начиная со второй записи, n-2 записи сравниваются для выбора записи с наименьшим ключевым словом из n-1 записей и обмениваются со второй таблицей записей. . При простом выборе i-го прохода, начиная с i-й записи, и при выборе записи с наименьшим ключевым словом из записей n-i + 1 путем сравнения ключевых слов n раз, и при выборе записи с i-й записью Записи обмениваются. Неоднократно, после того, как n-1 проходит простую сортировку выбора, n-1 записи сортируются на месте, а оставшаяся минимальная запись находится непосредственно в конце, поэтому требуется всего n-1 простых сортировок выбора.

 private static void SelectSort(int[] a) < int k=0,temp; for (int i = 0; i < a.length-1; i++) < k=i; for (int j = i+1; j < a.length; j++) < if(a[j]if(k!=i) < temp=a[i]; a[i]=a[k]; a[k]=temp; >> >

Анализ алгоритма: сравнение n-1 требуется, когда i = 1, сравнение n-2 требуется, когда i = 2, и n-1 + n-2 + .. + 1 = n (n-1) / 2, то есть операция сравненияВременная сложность O (n ^ 2), пространственная сложность O (1), нестабильная

2. Выбор дерева

Идея алгоритма: сортировка по дереву также называется турнирной сортировкой. Основная идея состоит в том, чтобы сравнить ключевые слова из n записей, которые должны быть отсортированы пара за парой, вынуть меньшую, а затем использовать тот же метод для сравнения среди [n / 2] более мелких и выбрать каждые две Меньшее повторяется до тех пор, пока не будет выбрана наименьшая запись ключевого слова. Этот процесс может быть представлен полным двоичным деревом. При неудовлетворенности он заполняется узлом с ключевым словом ∞. Наименьшей выбранной ключевой записью является корневой узел дерева. После вывода наименьшего ключевого слова, чтобы выбрать следующее наименьшее ключевое слово, значение ключевого слова конечного узла, соответствующего наименьшей записи ключевого слова, устанавливается равным ∞, а затем конечный узел сравнивается с ключевыми словами его родственных узлов. Измените значение каждого узла на пути от конечного узла к корневому узлу, тогда значением корневого узла является ключевое слово next-small. Повторяйте описанный выше процесс до тех пор, пока не будут выведены все записи. Процесс выбора наименьшего и наименьшего ключевых слов показан на рисунке.

(A) Выберите самые маленькие ключевые слова. (B) Выберите следующие маленькие ключевые слова. (B)

 private static void treeSelectSort(int[] a)< int len = a.length; int treeSize = 2 * len-1; // Количество узлов в полном двоичном дереве int low = 0; Object [] tree = new Object [treeSize]; // Место для временного дерева // Заполняем это дерево задом наперед, индекс начинается с 0 for(int i = len-1,j=0 ;i >= 0; --i,j++) < // Заполняем листовые узлы tree[treeSize-1-j] = a[i]; >for(int i = treeSize-1;i>0;i-=2) < // Заполняем нетерминальные узлы tree[(i-1)/2] = ((Comparable)tree[i-1]).compareTo(tree[i]) < 0 ? tree[i-1]:tree[i]; >// Постоянно удаляем самый маленький узел int minIndex; while(low < len)< Объект min = tree [0]; // Минимальное значение a[low++] = (int) min; minIndex = treeSize-1; // Находим индекс минимального значения while(((Comparable)tree[minIndex]).compareTo(min)!=0)< minIndex--; >tree [minIndex] = Integer.MAX_VALUE; // Установить максимальный флаг // Найти своих братьев и сестер while (minIndex> 0) else > > >

Анализ алгоритма: Предполагая, что глубина полного двоичного дерева, используемого для сортировки, равна h, при сортировке с выбором дерева, за исключением наименьшего ключевого слова, остальные выбранные меньшие ключевые слова сравниваются листовым узлом с корневым узлом. Процесс нужно сравнивать ч-1 раз. Можно доказать, что глубина полного двоичного дерева с n конечными узлами составляет h = log2n + 1, поэтому при упорядочении выбора дерева каждое меньшее выбранное ключевое слово необходимо сравнивать log2n раз, поэтому егоВременная сложность O (nlog2n) Пространственная сложность O (n) стабильная

3. Сортировка кучи

Уилломус также улучшил метод сортировки по дереву, heap sort, чтобы компенсировать недостатки сортировки по дереву, занимающие много места. При сортировке кучи требуется только одно вторичное пространство размера записи. Сортировка кучи — это обработка данных, хранящихся в векторе, как полного двоичного дерева в процессе сортировки, и использование внутренней связи между родительским узлом и дочерним узлом в полном двоичном дереве для выбора записи с наименьшим ключевым словом, то есть сортируемая запись по-прежнему использует Хранение векторного массива не использует древовидную структуру хранения, а использует только характеристики последовательной структуры полного двоичного дерева для анализа.

Идея алгоритма: ключевые слова сортируемых записей хранятся в массиве a [1, . n], а a рассматривается как последовательное представление полного двоичного дерева. Каждый узел представляет запись и первую запись a [0] является корнем двоичного дерева. Следующие записи a [1] ~ a [n-1] расположены в порядке слева направо в слоях. Левый потомок любого узла a [i] — это [2i], а правый Ребенок — [2i + 1], а родители — [i / 2]. Настройте и создайте это полностью двоичное дерево.

Определение кучи: Говорят, что значение ключа каждого узла удовлетворяет условию: a [i]> = a [2i] вырезает полное двоичное дерево [i]> a [2i + 1] как большую корневую кучу. И наоборот, куча, корневой узел которой меньше дочернего узла, называется маленькой корневой кучей. Например

Принцип реализации:

1. Сначала рассмотрим последовательность как древовидную структуру,

Процесс построения кучи: найдите последний нетерминальный узел n / 2 и сравните его с его левым и правым дочерними узлами,

Сравнение приводит к тому, что этот родительский узел является минимумом этих трех узлов. Найти н / 2-1 снова,

По сравнению с его левым и правым дочерними узлами получено минимальное значение и т. Д., А корневым узлом является минимальное значение.

Дерево после построения кучи

Порядок обмена данными: 97 49, 13 65,38 без изменений, 49 13,13 27

2. Выведите верхний элемент кучи и настройте процесс построения новой кучи

После вывода минимального значения в верхней части кучи предполагается, что оно будет заменено последним значением, поскольку структура кучи его левого и правого поддеревьев не была уничтожена

Это нужно только отрегулировать сверху вниз. Например, 13 на приведенном выше рисунке заменяется на 97, а затем можно заменить 97 и 27.

Затем происходит обмен 97 и 49. В это время минимальным значением является корневой элемент 27. После вывода 27 корневой элемент заменяется последним значением.

И так далее, и, наконец, получить упорядоченную последовательность

 private static void HeapSort(int[] a) < crt_heap(a); int temp; for (int i = a.length-1; i >=1; i--) < temp=a[0]; a[0]=a[i]; a[i]=temp; sift (a, 0, i-1); // сделать [0, . i-1] кучей >> // Восстановить кучу private static void sift(int[] a, int k, int m) < int t,x,i,j; t = a [k]; // Временная запись окурка a [k] x=a[k]; i=k; j=2*i; boolean finished=false; while (j  = a [j]) finish = true; // Завершение else > a [i] = t; // a [k] заполните соответствующую позицию > // Строим начальную кучу private static void crt_heap(int[] a) < int n=a.length-1; for (int i = n / 2; i>= 0; -i) >

Анализ алгоритма: в каждом цикле левое и правое поддеревья сравниваются один раз, а затем большее левое и правое поддеревья сравниваются с экранированными элементами, поэтому для кучи с глубиной H время сравнения ключей в алгоритме фильтрации До 2 (ч-1) раз.Временная сложность O (nlog2n) Пространственная сложность O (1) Нестабильный

Источник