Графы и деревья
Поскольку любое дерево является графом , то его можно задавать любым из способов, перечисленных в п. «Способы представления графов «. Однако существуют и специальные способы представления, предназначенные только для деревьев . Мы рассмотрим только два наиболее распространенных частных случая.
Представление корневого дерева
Этот способ подходит только для тех корневых деревьев , у которых точно известно максимальное количество потомков для любой вершины .
type ukazatel = ^tree; tree = record znachenie : integer; siblings : array[1..S] of ukazatel; end;
Разумеется, в общем случае значение переменной S (количество потомков ) может достигать N-1 ( N — количество всех вершин в дереве ). Однако ясно, что в такой ситуации особого смысла в динамической древесной структуре нет: экономии памяти не получается. Гораздо лучше, если у всех вершин примерно одинаковое и заранее известное количество потомков .
Представление бинарного дерева
Разновидностью описанного выше частного случая является бинарное корневое дерево : каждая его вершина имеет не более двух потомков :
type ukazatel = ^tree; tree = record znachenie : integer; left_sibling : ukazatel; right_sibling: ukazatel; end;
Примеры использования деревьев
Здесь мы ограничимся только примерами использования бинарных корневых деревьев : именно такой вид графа чаще всего применяется в программировании.
Дерево двоичного поиска
Дерево двоичного поиска для множества чисел S — это размеченное бинарное дерево , каждой вершине которого сопоставлено число из множества S , причем все пометки удовлетворяют следующим условиям:
- существует ровно одна вершина , помеченная любым числом из множества S ;
- все пометки левого поддерева строго меньше, чем пометка текущей вершины ;
- все пометки правого поддерева строго больше, чем пометка текущей вершины .
Если выражаться простым языком, то структура дерева двоичного поиска подчиняется простому правилу: «если больше — направо, если меньше — налево».
Например, для набора чисел 7 , 3 , 5 , 2 , 8 , 1 , 6 , 10 , 9 , 4 , 11 получится такое дерево (см. рис. 11.14).
Для того чтобы правильно учесть повторения чисел, можно ввести дополнительное поле, которое будет хранить количество вхождений для каждого числа.
Более подробно процессы построения и анализа дерева бинарного поиска будут изложены в следующей лекции, посвященной алгоритмам, использующим деревья и графы .
Дерево частотного словаря
Дерево частотного словаря — это результат построения дерева двоичного поиска не для чисел, а для слов некоторого текста. Генерирование дерева частотного словаря полезно при подсчете количества вхождений каждого слова в некоторый текст.
Приведем описание структуры этого дерева :
type ukazatel = ^tree; derevo = record slovo : string[20]; kolichestvo : integer; levyj : ukazatel; pravyj: ukazatel; end;
Дерево синтаксического анализа
Дерево синтаксического анализа арифметического выражения — это бинарное дерево , листьями которого служат операнды, а остальными вершинами — операции, причем уровень вершины соответствует приоритету выполнения операции: чем ближе к листьям , тем приоритет выше.
Например, на рис. 11.15 изображено дерево синтаксического анализа для выражения ((a / (b + c)) + (x * (y — z))) .
Деревья синтаксического разбора строятся компиляторами во время синтаксического анализа программ. Помимо арифметических выражений, которые являются простейшим случаем, аналогичные, но более сложные деревья строятся для всех грамматических конструкций компилируемой программы.
Источник
Способы изображения древовидной структуры
В данном разделе будут рассмотрены возможные варианты изображения деревьев. Из всех рассмотренных вариантов будет выбран один для реализации поставленной задачи. Этот способ должен быть достаточно удобен для восприятия, а также для реализации средствами языка программирования C++.
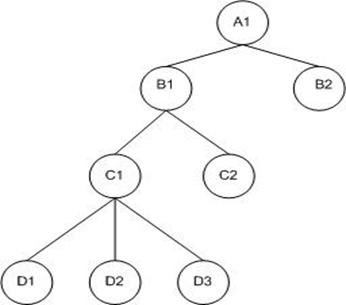
1) Первый способ, и наиболее распространенный – Классическая диаграмма (см. рисунок 2).
Рисунок 2 – Классическая диаграмма
2) Вложенные скобки. Легко реализуется на языках программирования, но неудобен для восприятия (см. Рисунок 3).
Рисунок 3 — Вложенные скобки
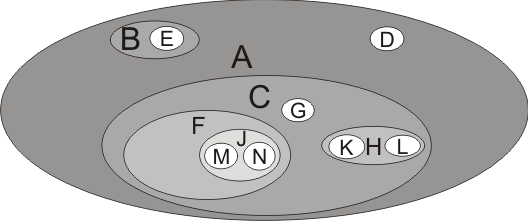
3) Вложенные множества. Данный способ наглядный и удобный для восприятия, но возможны проблемы с его реализацией (см. Рисунок 4).
Рисунок 4 — Вложенные множества
4) Ломаная последовательность (см. Рисунок 5).
Рисунок 5 — Ломаная последовательность
Двоичное (бинарное) дерево
Двоиичное деерево — древовидная структура данных, в которой каждый узел имеет не более двух потомков. Как правило, первый называется родительским узлом, а дети называются левым и правым наследниками.
То есть двоичное дерево либо является пустым, либо состоит из данных и двух поддеревьев (каждое из которых может быть пустым). Очевидным, но важным для понимания фактом является то, что каждое поддерево в свою очередь тоже является деревом. Если у некоторого узла оба поддерева пустые, то он называется листовым узлом (листовой вершиной).
Например, согласно этой грамматике, двоичное дерево можно было бы записать так (см. Рисунок 6):
Рисунок 6 — Двоичное дерево
Двоичное дерево поиска
Деревья двоичного поиска широко распространены в программировании. Значение содержимого каждой вершины дерева двоичного поиска:
1) Оба поддерева — левое и правое, являются двоичными деревьями поиска.
2) У всех узлов левого поддерева произвольного узла X значения ключей данных меньше, нежели значение ключа данных узла X.
3) У всех узлов правого поддерева произвольного узла X значения ключей данных больше, нежели значение ключа данных узла X.
Распространенность деревьев двоичного поиска в программировании является следствием эффективности методов поиска в этих деревьях.
Рисунок 7 — Двоичное дерево поиска
Разработка программного комплекса. Описание алгоритмов, используемых в программном комплексе
После анализа предметной области было решено использовать следующие языковые средства C++ для решения поставленной задачи:
- Для хранения вершин дерева с описанием связей – структуры. Структуры в С++ используются для логического и физического объединения данных произвольных типов, так же как массивы служат для группирования данных одного типа.
- Также нам потребуется возможность обходить все вершины, т.к. обход дерева придется осуществлять несколько раз, удобно будет вынести это действие в отдельную функцию и при необходимости вызывать ее в теле основной программы. По мере увеличения размера и сложности программного комплекса следует разделить его на небольшие легко управляемые части, называемые функциями. Каждая функция в вашей программе должна выполнять определенную задачу. Если программе необходимо выполнить определенную задачу, то она вызывает соответствующую функцию, обеспечивая эту функцию информацией, которая ей понадобится в процессе обработки.
Источник