Дерево Фенвика
Дерево Фенвика или двоичное индексированное дерево (англ. binary indexed tree) — структура данных, которая на многих задачах заменяет собой дерево отрезков, но при этом работает в 3-4 раза быстрее, занимает минимально возможное количество памяти (столько же, сколько и массив той же длины), намного быстрее пишется и легче обобщается на большие размерности.
#Определение
Пусть дан массив $a$ длины $n$. Деревом Фенвика будем называть массив $t$ той же длины, объявленный следующим образом:
где $F$ это какая-то функцию, для которой выполнено $F(i) \leq i$. Конкретно её определим потом.
Запрос суммы. Когда нам нужна сумма на отрезке, мы будем сводить этот запрос к двум суммам на префиксе:
$$ sum(l, r) = sum(r) — sum(l-1) $$ Оба этих запроса будем считать по формуле: $$ sum(k) = t_k + sum(F(k)-1) $$
Запрос обновления. Когда мы изменяем $k$-ю ячейку исходного массива, мы обновляем все $t_i$, в которых учтена эта ячейка.
$F$ можно выбрать так, что и «спусков» при подсчете суммы, и интересных нам $t_i$ при обновлении будет будет $O(\log n)$. Популярны две функции:
Первый вариант описан на Викиконспектах и Емаксе и поэтому более известен. Второй, как мы дальше увидим, более простой для запоминания и кодинга, а так же более гибкий — например, там можно делать бинпоиск по префиксным суммам. Его мы и будем использовать.
Примечание. Наверное, меньше четверти умеющих писать эту структуру полностью понимают, как она работает. Анализ действительно весьма сложный, поэтому мы приведём его в конце. Рекомендуется пока что абстрагироваться и принять на веру, что любой префикс разбивается на $O(\log n)$ отрезков вида $[F(i), i]$, а также что любой элемент входит в не более $O(\log n)$ таких отрезков.
#Реализация
Так как $F(0) = 1 > 0$, то $[0, F(0)]$ не является корректным отрезком. Поэтому нам будет удобнее хранить массив в 1-индексации и не использовать $t_0$.
Автор отмечает красивую симметрию в формулах r -= r & -r и k += k & -k , которой нет в «традиционной» версии.
#Многомерный случай
$k$-мерное дерево Фенвика пишется в $(k+1)$ строчку
Нужно добавить всего одну такую же строчку в sum , add , а также при подсчете суммы на прямоугольнике вместо двух запросов к префиксным суммам использовать четыре.
sum перепишется следующим образом:
В $k$-мерном случае, в соответствии с принципом включений-исключений, для запроса суммы нужно $2^k$ запросов суммы на префиксах.
Если размерности больше, чем позволяет память, то можно вместо массива t использовать хеш-таблицу — так потенциально потребуется $O(q \log^2 A)$ памяти ($A$ — максимальная координата), но это всё равно один из самых безболезненных способов решать достаточно простые задачи на двумерные структуры.
#Бинпоиск
Оказывается, можно производить бинарный поиск (точнее, спуск) по префиксным суммам за $O(\log n)$.
Если знать, что $F(x)$ удаляет последний бит $x$, то принцип понятен: просто делаем спуск по бинарному дереву, как в ДО. Чем-то похоже на генерацию $k$-го лексикографического комбинаторного объекта: пытаемся увеличить следующий символ всегда, когда это возможно.
Отметим, что в «традиционной» индексации такое делать нельзя.
#Ограничения на операцию
Дерево Фенвика можно использовать, когда наша операция обратима, а также когда трюк с префиксными суммами работает. Это обычно простые операции типа суммы, xor , умножения по модулю (если гарантируется, что на этот модуль ничего не делится). Минимум и gcd , отложенные операции и персистентность прикрутить в общем случае уже не получится — тогда уже нужно писать дерево отрезков.
#Почему это работает
Итак, мы выбрали вариант с $F(x)$ = x — (x & -x) + 1 . Поймем, что означает x & -x .
Лемма. x & -x возвращает последний единичный бит в двоичной записи x.
Доказательство потребует знания, как в компьютерах хранятся целые числа. Чтобы процессор не сжигал лишние такты, проверяя знак числа при арифметических операциях, их хранят как бы по модулю $2^k$, а первый бит отвечает за знак (0 для положительных и 1 для отрицательных). Поэтому когда мы хотим узнать, как выглядит отрицательное число, нужно его вычесть из нуля: $-x = 0-x = 2^k-x$.
Как будет выглядеть -x в битовой записи? Ответ можно мысленно разделить на три блока:
- Первые сколько-то (возможно, нисколько) нулей с конца числа x ими же в ответе и останутся.
- Потом, ровно на самом младшем единичном бите x, мы «займём» много единиц, так что весь префикс станет единицами. В ответе на этом месте точно будет единица.
- Потом отменятся ровно те биты из этого префикса, которые были единицами в исходном числе.
$$ \begin +90 = 2+8+16+64 & = 0 \, 10110_2 \\ -90 = 00000_2 — 10110_2 & = 1 \, 01010_2 \\ \implies (+90) \& (-90) & = 0 \, 00010_2 \end $$
Теперь мы можем доказать нашу лемму. Когда мы сделаем &, в префиксе до младшего единичного бита все биты x и -x будут противоположными, младший единичный бит останется единичным, а на суффиксе все как было нулями, так и осталось. Следовательно, «выживет» только этот самый младший единичный бит, что мы и доказывали.
Следствие 1. sum будет работать за логарифм, а точнее за количество единичных битов в записи $x$: на каждой итерации мы делаем x -= x & -x , то есть удаляем младший бит.
Следствие 2. add тоже будет работать за логарифм: каждую итерацию количество нулей на конце $x$ увеличивается хотя бы на единицу.
Следствие 3. (Почему дерево Фенвика — дерево.)
- Длина отрезка, соответствующего любому $t_i$ — степень двойки, причём начинается этот отрезок на индексе, кратном этой же степени двойки.
- $\implies$ Множества элементов, учтённых в произвольных $t_i$ и $t_j$, либо не пересекаются, либо одно является подмножеством другого.
- $\implies$ На $t_i$ можно ввести отношение вложенности.
То есть, если напрячь воображение, то $t$ можно рассматривать как лес деревьев. В частном случае, когда $n$ является степенью двойки, дерево будет одно.
Теперь единственное, что осталось доказать — это корректность add . На самом деле, в add мы делаем ни что иное, как подъём от вершины до корня по всем предкам.
Как для $x$ найти непосредственного родителя? Нужно найти минимальное число $y > x$, у которого $t_y$ будет включать $x$. Иными словами, должно выполняться y >= x > y — (y & -y) .
Дальше читателю предлагается самостоятельно попялиться в пример, чтобы понять, что x + (x & -x) — минимальное такое число:
$$ \begin x = 90 = 2+8+16+64 & = 10110_2 \\\ y = 96 = 32 + 64 & = 11000_2 \end $$
Источник
Дерево Фенвика
Здравствуй, Хабрахабр. Сейчас я хочу рассказать о такой структуре данных как дерево Фенвика. Впервые описанной Питером Фенвиком в 1994 году. Данная структура похожа на дерево отрезков, но проще в реализации.
Что это?
Дерево Фенвика — это структура данных, дерево на массиве, которая обладает следующими свойствами:
• позволяет вычислять значение некоторой обратимой операции F на любом отрезке [L; R] за логарифмическое время;
• позволяет изменять значение любого элемента за O(log N);
• требует памяти O(N);
операция F
Операция F может быть выбрана разными способами, но чаще всего берутся операции суммы интервала, произведение интервала, а также при определенной модификации и ограничениях, нахождения максимума и нахождения минимума на интервале или другие операции.
Простейшая задача
Рассмотрим задачу о нахождения суммы последовательных элементов массива. С учетом того, что будет много запросов, вида (L,R), где требуется найти S(L,R)- сумму всех элементов с a[L] до a[R] включительно.
Простейшим решением данной задачи будет нахождение частичных сумм. После их нахождения запишем эти суммы в массив, в котором sum[i]=a[1]+a[2]. +a[i]. Тогда требуемая в запросе величина S(L,R)=sum[R]-sum[L-1] (sum[0] обычно считают равной нулю, чтобы не рассматривать отдельных случаев).
Недостатки
Но у данной реализации этой задачи есть существенные недостатки. И один из главных заключается в том, что при изменении одного элемента исходного массива, приходится пересчитывать в среднем O(N) частичных сумм, а это затратно по времени. Вот для решения этой проблемы можно использовать дерево Фенвика.
Преимущества
Главным преимуществом данной конструкции является простота реализации и быстрота ответов на запросы (за O(1)).
Применения дерева Фенвика для данной задачи
Введем функцию G(x), которая определена в натуральных числах, и равна x&(x+1) (&- побитовое И). Таким образом, G(x) равна x, если в двоичном разложении x последним стоит 0 (x делится на 2). А если в двоичном разложении x в младших разрядах идет группа единиц, то функция равна x с замененными последними единицами на 0. Можно убедиться на примерах, что это и есть x&(x+1) (смотрите рисунок).
Теперь будем считать следующие частичные суммы, и записывать их в t[i]=a[G[i]]+a[G[i]+1]…+a[i]. Далее будет показано как находить эти суммы.
Подсчет суммы
Чтобы найти S(L,R), будем искать S(1,L-1) и S(1,R). Напишем функцию, которая при наличии массива t, будет находить S(L,R). В данном случае левый конец не будет включен в сумму, но его легко включить если это требуется в задаче (смотрите код).
const int N=100; int t[N],a[N]; int sum(int L, int R) < int res=0; while (R >= 0) < res += t[R]; R = G( R ) - 1; >while (L >= 0) < res -= t[L]; L = G(L) - 1; >return res; > Так же стоит заметить, что функция G за каждое применение уменьшает количество единиц в двоичной записи x, как минимум на 1. Из чего следует, что подсчет суммы будет произведен за O(log N).
Модификация элементов
Теперь рассмотрим модификацию элементов. Нам надо научиться быстро изменять частичные суммы в зависимости от того, как изменяются элементы. Мы будем изменять a[k] на величину d. Тогда нам надо изменить элементы массива t[j], для которых верно неравенство G(j) 
Где под | понимают побитовое ИЛИ. 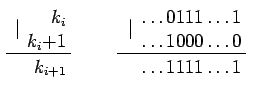
Несложно заметить, что данная функция строго возрастает и в худшем случае будет применена логарифм раз, так как добавляет каждый раз по одной единице в двоичном разложении числа k.
Напишем функцию, которая будет изменять a[k] элемент на d, и при этом меняет соответствующие частичные суммы.
const int N=100; int t[N],a[N]; void upd(int k, int d) < a[k]+=d; while(k> Инициализация
Теперь заметим, что при первоначальном подсчете массива t, возможна его инициализация нулями. После чего, применяем для каждого из N элементов функцию upd(i,a[i]). Тогда, на первоначальный подсчет уйдет O(N*log N) времени, что больше чем у описанного алгоритма с простыми частичными суммами.
Сравнение с деревом отрезков
Преимущества:
— уже упомянутая простота и скорость
— памяти занимает O(N)
Недостатки:
— функция должна быть обратимой, а это значит, что минимум и максимум это дерево считать не может (за исключением случаев, когда некоторыми данными мы можем пожертвовать).
Заключение
Мы научились отвечать на запросы о сумме элементов и модифицировать любой элемент за логарифмическое время. Данный алгоритм имеет множество применений, и может помочь во всех задачах, где надо быстро изменять и определять результат операции. Надеюсь, всем было понятно и интересно. Спасибо за внимание.
Источник
