Персистентные деревья отрезков
Структуры данных можно разделить на две группы: эфемерные (ephemeral) и персистентные (persistent).
Эфемерными называются структуры данных, хранящие только последнюю свою версию.
Персистентные структуры, то есть те, которые сохраняют все свои предыдущие версии, в свою очередь можно разделить еще на две подгруппы: если структура данных, позволяет изменять только последнюю версию, она называется частично персистентной (partially persistent), если же позволяется изменять любую версию, такая структура считается полностью персистентной (fully persistent).
Далее будет рассмотрено дерево отрезков и его полностью персистентная версия.
Весь код доступен на GitHub.
Дерево отрезков
Те, кто уже знаком с деревьями отрезков, могут сразу перейти к разделу о персистентной версии.
Деревом отрезков называется структура данных, позволяющая для данного массива A быстро выполнять следующие операции:
Описание
Пусть n — длина массива A , будем заполнять его нейтральными элементами до тех пор, пока его длина не станет равна степени двойки (например, если f — сумма, массив будет дополняться нулями).
Теперь построим такое двоичное дерево, что его листьями будут все элементы A и глубина всех листьев одинакова, а во всех остальных вершинах будут храниться значения f от значений дочерних вершин.
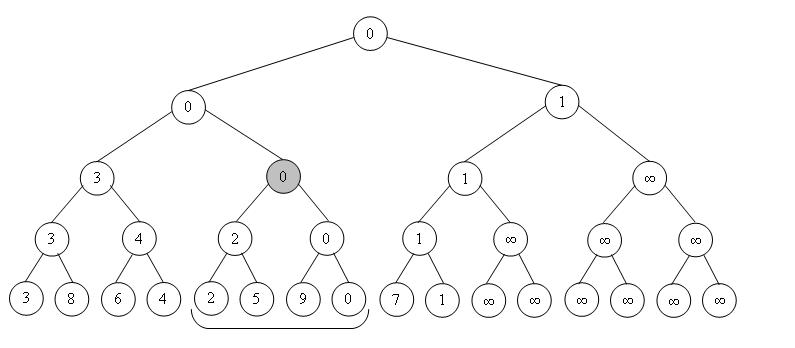
Рассмотрим в качестве примера дерево отрезков для массива A = [4, 1, 4, 2, 5, 3] :
Хранить такое дерево удобно как и двоичную кучу: в виде массива вершин, записанных подряд сверху вниз слева направо:
19 11 8 5 6 8 0 4 1 4 2 5 3 0 0
В таком случае для вершины с индексом i ее предком будет вершина ((i — 1) / 2) , а левый и правый дочерние вершины будут иметь индексы (2 * i + 1) и (2 * i + 2) соответственно (считая, что элементы в массиве нумеруются с нуля).
Построение
Удобно строить дерево отрезков рекурсивно сверху вниз: для каждой вершины построить левую и правую дочерние вершины, после чего посчитать значение f от их значений, а для листов же просто записать соответствующее значение массива в дерево.
Строя дерево таким образом каждая вершина будет посещена один раз, и, так как количество вершин в дереве Θ(n), сложность построения также Θ(n).
Изменение
После того, как было изменено значение какого-либо элемента, в дереве могли испортиться некоторые из значений предков данного элемента. Исправить это можно, пересчитав значения предков данного элемента, поднимаясь по дереву снизу вверх.
Например, если в массиве A заменить A[3] на 10 , то будут пересчитаны вершины со значениями 6 , 11 и 19 .
Так как высота дерева log n, то операция изменения затронет ровно log n вершин, значит, асимптотика операции O(log n).
Вычисление F
Данная операция будет выполняться рекурсивно сверху вниз.
Пусть в произвольной вершине v посчитано F для диапазона l..r , тогда нетрудно проверить, что в левой дочерней вершине посчитано значение F для l..((l + r) / 2) , а в правой — для ((l + r) / 2 + 1)..r .
Предположим, что поступил запрос F(i, j) , и текущая вершина — v . Возможны два случая:
- В узле v уже посчитано значение F(i, j) . Тогда ответом на полученный запрос будет значение вершины v .
- В узле v записано F для большего диапазона. В таком случае рекурсивно вызовем вычисление F(i, (l + r) / 2) для левого дочерней вершины и F((l + r) / 2 + 1, j) для правой, и ответом будет f от этих двух значений.
Пример
Персистентное дерево отрезков
Добиться персистентности можно разными способами, самый простой из них — при каждом изменении делать полную копию старой версии и изменять ее, как обычное дерево отрезков, однако такой способ слишком затратен по памяти и ухудшает асимптотику операции Change до O(n).
Построение
Построение персистентного дерева отрезков будет аналогично построению обычного дерева отрезков за исключением того, что теперь для каждой вершины дополнительно придется в явном виде хранить ссылки на дочерние вершины.
Также дополнительно понадобится хранить массив вершин, являющихся корнями в соответствующих версиях дерева. При построении в него добавляется единственная вершина, являющаяся корнем полученного дерева.
Так как единственное изменение по сравнению с эфемерным деревом отрезков — это добавление информации о левой и правой дочерних вершинах, сложность построения осталось неизменной, то есть Θ(n).
Изменение
Вместо полного копирования дерева при изменении вершины к нему будут добавлены только те вершины, которые должны были измениться, и вместо изменения значений старых вершин, пересчитанные значения будут сохранены в новые. Все новые вершины будут ссылаться на одну вершину из дерева старой версии и на одну из только что добавленных.
Добавление новой ветки делается аналогично построению всего дерева за исключением того, что вместо построения двух дочерних вершин, новая вершина строится только в том направлении, в котором лежит измененная вершина.
После этого обновляется массив корневых вершин.
Так как при изменении только добавляется log n вершин, асимптотика операции — O(log n).
Вычисление F
Вычисление F производится аналогично эфемерному дереву. Единственные отличия: переходы к дочерним вершинам и запуск из разных корневых вершин.
Отсюда следует сложность O(log n).
Пример
Задачи
При помощи персистентного дерева отрезков можно решить задачу «Откат» (разбор задачи). Решение задачи с использованием приведенной выше реализации персистентного дерева отрезков доступно на GitHub.
Также здесь можно прочитать обсуждение задачи о k-ой порядковой статистике на диапазоне.
Источник
Дерево отрезков. Построение
Дерево отрезков (англ. Segment tree) — это структура данных, которая позволяет за асимптотику [math]O(\log n)[/math] реализовать любые операции, определяемые на множестве, на котором данная операция ассоциативна, и существует нейтральный элемент относительно этой операции, то есть на моноиде. Например, суммирование на множестве натуральных чисел, поиск минимума на любом числовом множестве, перемножение матриц на множестве матриц размера [math]N*N[/math] , объединение множеств, поиск наибольшего общего делителя на множестве целых чисел и многочленов.
При этом дополнительно возможно изменение элементов массива: как изменение значения одного элемента, так и изменение элементов на целом подотрезке массива, например разрешается присвоить всем элементам [math]a[l \ldots r][/math] какое-либо значение, либо прибавить ко всем элементам массива какое-либо число. Структура занимает [math]O(n)[/math] памяти, а ее построение требует [math]O(n)[/math] времени.
Структура
Структура представляет собой дерево, листьями которого являются элементы исходного массива. Другие вершины этого дерева имеют по [math]2[/math] ребенка и содержат результат операции от своих детей (например минимум или сумму). Таким образом, корень содержит результат искомой функции от всего массива [math][0\ldots n-1][/math] , левый ребёнок корня содержит результат функции на [math][0\ldots\dfrac][/math] , а правый, соответственно результат на [math][\dfrac+1\ldots n-1][/math] . И так далее, продвигаясь вглубь дерева.
Построение дерева
Пусть исходный массив [math]a[/math] состоит из [math]n[/math] элементов. Для удобства построения увеличим длину массива [math]a[/math] так, чтобы она равнялась ближайшей степени двойки, т.е. [math]2^k[/math] , где [math]2^k \geqslant n[/math] . Это сделано, для того чтобы не допустить обращение к несуществующим элементам массива при дальнейшем процессе построения. Пустые элементы необходимо заполнить нейтральными элементами моноида. Тогда для хранения дерева отрезков понадобится массив [math]t[/math] из [math]2^[/math] элементов, поскольку в худшем случае количество вершин в дереве можно оценить суммой [math]n+\dfrac+\dfrac \ldots +1 \lt 2n[/math] , где [math]n=2^k[/math] . Таким образом, структура занимает линейную память.
Выделяют два основных способа построения дерева отрезков: построение снизу и построение сверху. При построении снизу алгоритм поднимается от листьев к корню (Просто начинаем заполнять элементы массива [math]t[/math] от большего индекса к меньшему, таким образом при заполнении элемента [math] i [/math] его дети [math]2i+1[/math] и [math]2i+2[/math] уже будут заполнены, и мы с легкостью посчитаем бинарную операцию от них), а при построении сверху спускается от корня к листьям. Особенные изменения появляются в реализации запросов к таким деревьям отрезков.
Реализация построения сверху:
function treeBuild(T a[], int i, int tl, int tr): // мы находимся в вершине с номером i, который отвечает за полуинтервал [tl, tr) if tr - tl == 1 t[i] = a[tl] else tm = (tl + tr) / 2 // середина отрезка treeBuild(a, 2 * i + 1, tl, tm) treeBuild(a, 2 * i + 2, tm, tr) t[i] = t[2 * i + 1] t[2 * i + 2] Реализация построения снизу:
function treeBuild(T a[]): for i = 0 to n - 1 t[n - 1 + i] = a[i] for i = n - 2 downto 0 t[i] = t[2 * i + 1] t[2 * i + 2] См. также
Источники информации
Источник
![Дерево отрезков для массива [4, 1, 4, 2, 5, 3]](https://habrastorage.org/storage2/549/053/b2f/549053b2f992ca7dae0fd0f6013b51ed.png)
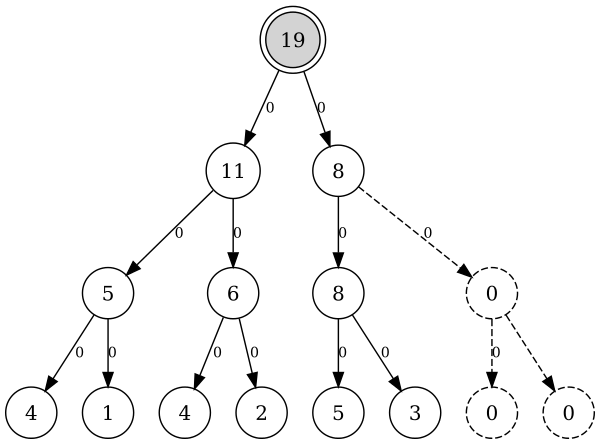
![Персистентное дерево отрезков, версия 1 (A[3] = 10)](https://habrastorage.org/storage2/0c8/68b/0aa/0c868b0aa3d58afe2ef715d1b0f6c18e.png)