Структуры данных деревья кучи

Структуры данных: 2-3 куча (2-3 heap)

Вопрос эффективного способа реализации очереди с приоритетом некоторой структурой данных остается актуальным в течении долгого времени. Ответ на данный вопрос всегда является неким компромиссом между объёмом памяти, необходимым для хранения данных и временем работой операций над очередью.

В компьютерных науках для эффективной реализации очереди с приоритетом используются структуры в виде кучи.

Куча — это специализированная структура данных типа дерево, которая удовлетворяет свойству кучи: если B является узлом-потомком узла A, то ключ(A) ≥ ключ(B). Из этого следует, что элемент с наибольшим ключом всегда является корневым узлом кучи, поэтому иногда такие кучи называют max-кучами (в качестве альтернативы, если сравнение перевернуть, то наименьший элемент будет всегда корневым узлом, такие кучи называют min-кучами). Не существует никаких ограничений относительно того, сколько узлов-потомков имеет каждый узел кучи, хотя на практике их число обычно не более двух. Кучи имеют решающее значение в некоторых эффективных алгоритмах на графах, таких как алгоритм Дейкстры и сортировка методом пирамиды.

Одними из наиболее изученных и хорошо зарекомендовавших себя структур данных для хранения и работой с очередью с приоритетом являются Бинарная Куча (Binary Heap) и Куча Фибоначчи (Fibonacci Heap). Но данные структуры обладают некоторыми особенностями.

Например, бинарная куча для основных операций имеет трудоемкость Θ(logn), кроме нахождения минимального, а для слияния таких куч потребуется линейное время (!). Зато для хранения такой кучи необходимо мало памяти по сравнению с другими кучами.

Куча Фибоначчи обладает балансировкой при извлечении узла из кучи, что позволяет сократить трудоемкость основных операций. При большом количестве последовательных операций добавления Фибоначчиева куча растет в ширину и балансировка происходит лишь при операции удаления минимума, поэтому операция получения минимума может потребовать значительных затрат времени!

Решением над этой проблемой занялся Тадао Такаока (Tadao Takaoka), опубликовав свою работу «2-3 heap» в 1999 году…

Немного о структуре «2-3 Heap»

2-3 куча (2-3 heap) — это структура данных типа дерево, которая удовлетворяет свойству кучи (min-heap, max-heap). Является альтернативой кучи Фибоначчи (Fibonacci heap). Состоит из 2-3 деревьев.

Решение, которое предлагает 2-3 heap, заключается в том, что в отличии от Кучи Фибоначчи, 2-3 куча выполняет балансировку не только при удалении, но и при добавлении новых элементов, снижая вычислительную нагрузку при извлечении минимального узла из кучи.

Количество детей вершины t произвольного дерева T назовем степенью (degree) этой вершины, а степенью дерева назовем степень его корня.

2-3 деревьями называются деревья T₀, T₁, T₂, . определенные индуктивно. Дерево T₀ состоит из единственной вершины. Под деревом T_i понимается дерево, составленное либо из двух деревьев T_i-1 либо из трех: при этом корень каждого следующего становится самым правым ребенком корня предыдущего.

Деревьями 2-3 кучи назовем деревья H[i]. Дерево H[i] — это либо пустое 2-3 дерево, либо одно, либо два 2-3 дерева степени i, соединенные аналогично деревьям T_i.

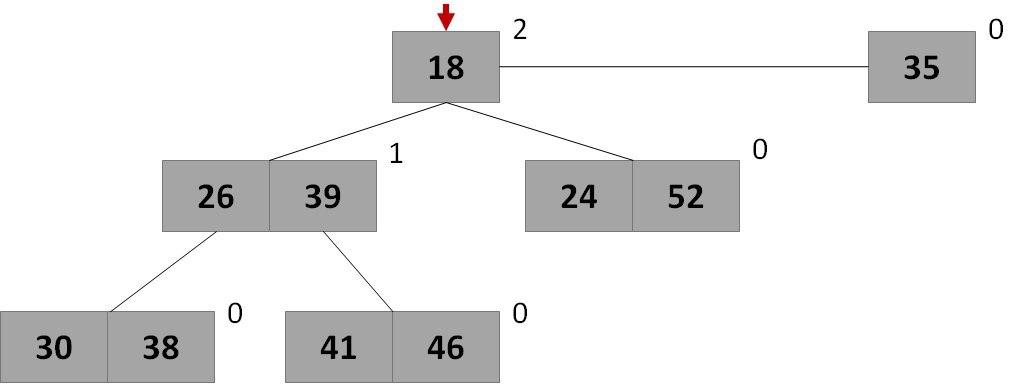
2-3 куча – это массив деревьев H[i] (i=0..n), для каждого из которых выполняется свойство кучи.

рис. Визуальное представление кучи

Структура узла

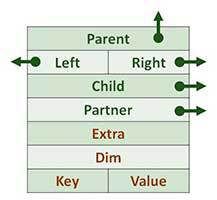Каждый узел имеет указатели на другие узлы (поля имеющие стрелки), служебные поля и пара ключ (приоритет) – значение.

Основные операции

Поиск минимального в 2-3 heap (FindMin)

Минимальный элемент кучи находится в корне одного из деревьев кучи. Чтобы найти минимальный узел, нужно пройтись по деревьям.

Поддерживая указатель на минимальный узел в куче мы можем находить этот узел за константное время ( Θ(1) )

Вставка в 2-3 heap (Insert)

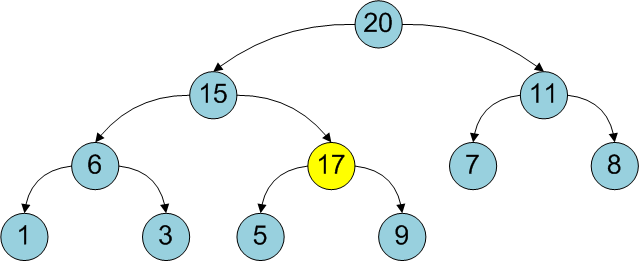
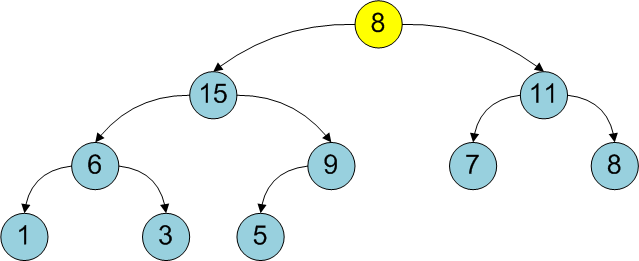
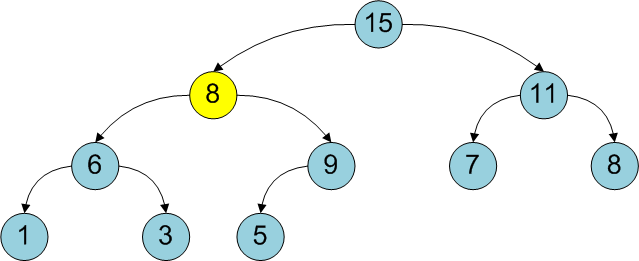
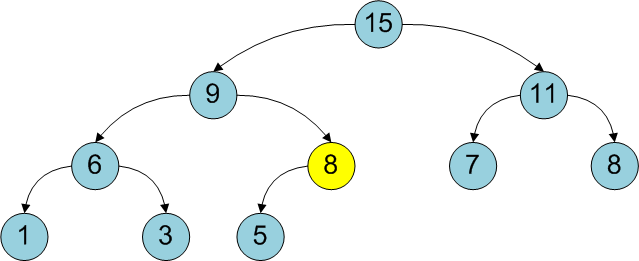
1. Для добавления нового элемента создадим дерево H[0] содержащее одну вершину
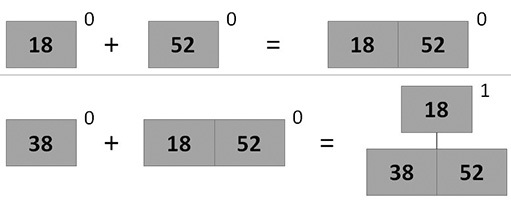
2. Произведем операцию добавления этого дерева в кучу. При добавлении дерева степени i в кучу возможны следующие варианты:
   1. Если дерева с таким приоритетом нет, то просто его добавляем в кучу.
   2. Иначе извлекаем такое дерево из кучи и соединяем с добавляемым, после добавляем полученное дерево в кучу
3. После добавление поправляем указатель на минимальный корень

рис. Анимация последовательного добавления элементов в 2-3 кучу

Удаление минимального элемента из кучи

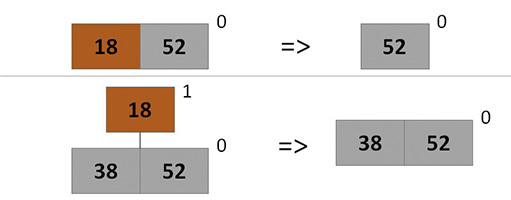
Минимальный элемент кучи находится в корне одного из деревьев кучи, допустим в H[i] – найдем его с помощью FindMin. Извлечем дерево H[i] из кучи и удалим его корень, при этом дерево распадется на поддеревья, которые мы впоследствии добавим в кучу.

Будем удалять корень рекурсивно: если дерево состоит из одной вершины, то просто удалим её; иначе отсоединяем от корня самого правого ребенка и продолжим удаление.

Уменьшение ключа у элемента

Первым делом мы можем свободно уменьшить ключ у необходимого узла. После этого необходимо проверить: если узел находится в корне дерева, то более ничего делать не нужно, иначе нужно будет извлечь этот узел со всеми поддеревьями и вставить его обратно в кучу (с уже измененным ключом).

Объединение двух куч в одну

Имеется две кучи, которые нужно объединить в одну. Для этого мы будем по очереди извлекаем все 2-3 деревья из второй кучи и вставлять их в первую кучу. После нужно будет поправить счетчик количества узлов: суммируем количество элементов в первой и во второй куче и записываем результат в счетчик в первой куче, а во второй куче устанавливаем счетчик в 0.

Сравнение трудоемкостей операций с другими алгоритмами

В таблице приведены трудоемкости операций очереди с приоритетом (в худшем случае, worst case)
Символом ‘*’ отмечена амортизированная сложность операций

Операция	Binary Heap	Binomial Heap	Fibonacci Heap	2-3 Heap
FindMin	Θ(1)	O(logn)	Θ(1)*	Θ(1)*
DeleteMin	Θ(logn)	Θ(logn)	O(logn)*	O(logn)*
Insert	Θ(logn)	O(logn)	Θ(1)*	Θ(1)*
DecreaseKey	Θ(logn)	Θ(logn)	Θ(1)*	Θ(1)*
Merge/Union	Θ(n)	Ω(logn)	Θ(1)	Θ(1)*

Спасибо за уделенное внимание!

Исходный код реализации на C++, основанной на статье автора 2-3 Heap доступен на GitHub под MIT.

PS: При написании курсового проекта по этой теме, я понял, что информации в Рунете практически нет, поэтому решил внести свои пару копеек в это дело, рассказав заинтересованному сообществу об этом алгоритме.

Источник

Структуры данных: двоичная куча (binary heap)

Двоичная куча (binary heap) – просто реализуемая структура данных, позволяющая быстро (за логарифмическое время) добавлять элементы и извлекать элемент с максимальным приоритетом (например, максимальный по значению).

Для дальнейшего чтения необходимо иметь представление о деревьях, а также желательно знать об оценке сложности алгоритмов. Алгоритмы в этой статье будут сопровождаться кодом на C#.

Введение

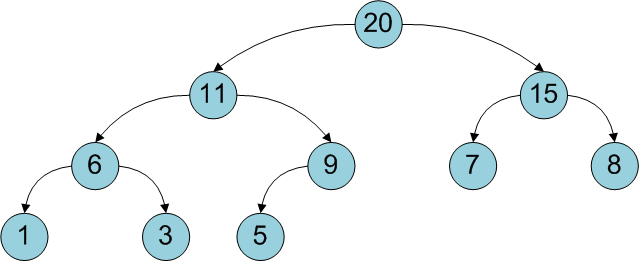
Двоичная куча представляет собой полное бинарное дерево, для которого выполняется основное свойство кучи: приоритет каждой вершины больше приоритетов её потомков. В простейшем случае приоритет каждой вершины можно считать равным её значению. В таком случае структура называется max-heap, поскольку корень поддерева является максимумом из значений элементов поддерева. В этой статье для простоты используется именно такое представление. Напомню также, что дерево называется полным бинарным, если у каждой вершины есть не более двух потомков, а заполнение уровней вершин идет сверху вниз (в пределах одного уровня – слева направо).

Двоичную кучу удобно хранить в виде одномерного массива, причем левый потомок вершины с индексом i имеет индекс 2*i+1 , а правый 2*i+2 . Корень дерева – элемент с индексом 0. Высота двоичной кучи равна высоте дерева, то есть log₂ N, где N – количество элементов массива.

Приведу заготовку класса на C#:

public class BinaryHeap < private Listlist; public int heapSize < get < return this.list.Count(); >> > 

Добавление элемента

Новый элемент добавляется на последнее место в массиве, то есть позицию с индексом heapSize :

Возможно, что при этом будет нарушено основное свойство кучи, так как новый элемент может быть больше родителя. В таком случае следует «поднимать» новый элемент на один уровень (менять с вершиной-родителем) до тех пор, пока не будет соблюдено основное свойство кучи:

Иначе говоря, новый элемент «всплывает», «проталкивается» вверх, пока не займет свое место. Сложность алгоритма не превышает высоты двоичной кучи (так как количество «подъемов» не больше высоты дерева), то есть равна O(log₂ N).

public void add(int value) < list.Add(value); int i = heapSize - 1; int parent = (i - 1) / 2; while (i >0 && list[parent] < list[i]) < int temp = list[i]; list[i] = list[parent]; list[parent] = temp; i = parent; parent = (i - 1) / 2; >> 

Упорядочение двоичной кучи

В ходе других операций с уже построенной двоичной кучей также может нарушиться основное свойство кучи: вершина может стать меньше своего потомка.

Метод heapify восстанавливает основное свойство кучи для дерева с корнем в i-ой вершине при условии, что оба поддерева ему удовлетворяют. Для этого необходимо «опускать» i-ую вершину (менять местами с наибольшим из потомков), пока основное свойство не будет восстановлено (процесс завершится, когда не найдется потомка, большего своего родителя). Нетрудно понять, что сложность этого алгоритма также равна O(log₂ N).

public void heapify(int i) < int leftChild; int rightChild; int largestChild; for (; ; ) < leftChild = 2 * i + 1; rightChild = 2 * i + 2; largestChild = i; if (leftChild < heapSize && list[leftChild] >list[largestChild]) < largestChild = leftChild; >if (rightChild < heapSize && list[rightChild] >list[largestChild]) < largestChild = rightChild; >if (largestChild == i) < break; >int temp = list[i]; list[i] = list[largestChild]; list[largestChild] = temp; i = largestChild; > > 

Построение двоичной кучи

Наиболее очевидный способ построить кучу из неупорядоченного массива – это по очереди добавить все его элементы. Временная оценка такого алгоритма O(N log₂ N). Однако можно построить кучу еще быстрее — за О(N). Сначала следует построить дерево из всех элементов массива, не заботясь о соблюдении основного свойства кучи, а потом вызвать метод heapify для всех вершин, у которых есть хотя бы один потомок (так как поддеревья, состоящие из одной вершины без потомков, уже упорядочены). Потомки гарантированно есть у первых heapSize/2 вершин.

public void buildHeap(int[] sourceArray) < list = sourceArray.ToList(); for (int i = heapSize / 2; i >= 0; i--) < heapify(i); >> 

Извлечение (удаление) максимального элемента

В упорядоченном max-heap максимальный элемент всегда хранится в корне. Восстановить упорядоченность двоичной кучи после удаления максимального элемента можно, поставив на его место последний элемент и вызвав heapify для корня, то есть упорядочив все дерево.

Сортировка с применением двоичной кучи

Заметим, что можно отсортировать массив, сначала построив из него двоичную кучу, а потом последовательно извлекая максимальные элементы. Оценим временную сложность такого элемента: построение кучи – O(N), извлечение N элементов – O(N log₂ N). Следовательно, итоговая оценка O(N log₂ N). При этом дополнительная память для массива не используется.

public void heapSort(int[] array) < buildHeap(array); for (int i = array.Length - 1; i >= 0; i--) < array[i] = getMax(); heapify(0); >> 

Заключение

Таким образом, двоичная куча имеет структуру дерева логарифмической высоты (относительно количества вершин), позволяет за логарифмическое же время добавлять элементы и извлекать элемент с максимальным приоритетом за константное время. В то же время двоичная куча проста в реализации и не требует дополнительной памяти.

Источник