Структуры данных очередь бинарное дерево

10 типов структур данных, которые нужно знать + видео и упражнения

Екатерина Малахова, редактор-фрилансер, специально для блога Нетологии адаптировала статью Beau Carnes об основных типах структур данных.

«Плохие программисты думают о коде. Хорошие программисты думают о структурах данных и их взаимосвязях», — Линус Торвальдс, создатель Linux.

Структуры данных играют важную роль в процессе разработки ПО, а еще по ним часто задают вопросы на собеседованиях для разработчиков. Хорошая новость в том, что по сути они представляют собой всего лишь специальные форматы для организации и хранения данных.

В этой статье я покажу вам 10 самых распространенных структур данных. Для каждой из них приведены видео и примеры их реализации на JavaScript. Чтобы вы смогли попрактиковаться, я также добавил несколько упражнений из бета-версии новой учебной программы freeCodeCamp.

Обратите внимание, что некоторые структуры данных включают временную сложность в нотации «большого О». Это относится не ко всем из них, так как иногда временная сложность зависит от реализации. Если вы хотите узнать больше о нотации «большого О», посмотрите это видео от Briana Marie.

В статье я привожу примеры реализации этих структур данных на JavaScript: они также пригодятся, если вы используете низкоуровневый язык вроде С. В многие высокоуровневые языки, включая JavaScript, уже встроены реализации большинства структур данных, о которых пойдет речь. Тем не менее, такие знания станут серьезным преимуществом при поиске работы и пригодятся при написании высокопроизводительного кода.

Связные списки

Связный список — одна из базовых структур данных. Ее часто сравнивают с массивом, так как многие другие структуры можно реализовать с помощью либо массива, либо связного списка. У этих двух типов есть преимущества и недостатки.

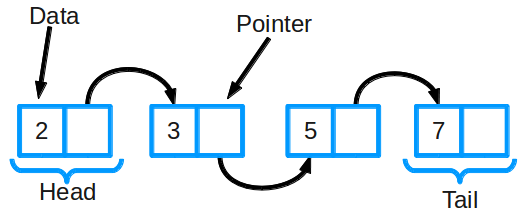
Так устроен связный список

Связный список состоит из группы узлов, которые вместе образуют последовательность. Каждый узел содержит две вещи: фактические данные, которые в нем хранятся (это могут быть данные любого типа) и указатель (или ссылку) на следующий узел в последовательности. Также существуют двусвязные списки: в них у каждого узла есть указатель и на следующий, и на предыдущий элемент в списке.

Основные операции в связном списке включают добавление, удаление и поиск элемента в списке.

Временная сложность связного списка ╔═══════════╦═════════════════╦═══════════════╗ ║ Алгоритм ║Среднее значение ║ Худший случай ║ ╠═══════════╬═════════════════╬═══════════════╣ ║ Space ║ O(n) ║ O(n) ║ ║ Search ║ O(n) ║ O(n) ║ ║ Insert ║ O(1) ║ O(1) ║ ║ Delete ║ O(1) ║ O(1) ║ ╚═══════════╩═════════════════╩═══════════════╝ 

Упражнения от freeCodeCamp

Стеки

Стек — это базовая структура данных, которая позволяет добавлять или удалять элементы только в её начале. Она похожа на стопку книг: если вы хотите взглянуть на книгу в середине стека, сперва придется убрать лежащие сверху.

Стек организован по принципу LIFO (Last In First Out, «последним пришёл — первым вышел») . Это значит, что последний элемент, который вы добавили в стек, первым выйдет из него.

Так устроен стек

В стеках можно выполнять три операции: добавление элемента (push), удаление элемента (pop) и отображение содержимого стека (pip).

Временная сложность стека ╔═══════════╦═════════════════╦═══════════════╗ ║ Алгоритм ║Среднее значение ║ Худший случай ║ ╠═══════════╬═════════════════╬═══════════════╣ ║ Space ║ O(n) ║ O(n) ║ ║ Search ║ O(n) ║ O(n) ║ ║ Insert ║ O(1) ║ O(1) ║ ║ Delete ║ O(1) ║ O(1) ║ ╚═══════════╩═════════════════╩═══════════════╝ 

Упражнения от freeCodeCamp

Очереди

Эту структуру можно представить как очередь в продуктовом магазине. Первым обслуживают того, кто пришёл в самом начале — всё как в жизни.

Так устроена очередь

Очередь устроена по принципу FIFO (First In First Out, «первый пришёл — первый вышел»). Это значит, что удалить элемент можно только после того, как были убраны все ранее добавленные элементы.

Очередь позволяет выполнять две основных операции: добавлять элементы в конец очереди (enqueue) и удалять первый элемент (dequeue).

Временная сложность очереди ╔═══════════╦═════════════════╦═══════════════╗ ║ Алгоритм ║Среднее значение ║ Худший случай ║ ╠═══════════╬═════════════════╬═══════════════╣ ║ Space ║ O(n) ║ O(n) ║ ║ Search ║ O(n) ║ O(n) ║ ║ Insert ║ O(1) ║ O(1) ║ ║ Delete ║ O(1) ║ O(1) ║ ╚═══════════╩═════════════════╩═══════════════╝ 

Упражнения от freeCodeCamp

Множества

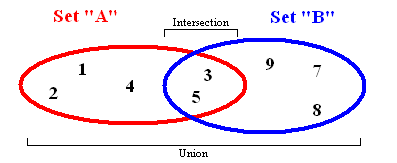
Так выглядит множество

Множество хранит значения данных без определенного порядка, не повторяя их. Оно позволяет не только добавлять и удалять элементы: есть ещё несколько важных функций, которые можно применять к двум множествам сразу.

• Объединение комбинирует все элементы из двух разных множеств, превращая их в одно (без дубликатов).
• Пересечение анализирует два множества и создает еще одно из тех элементов, которые присутствуют в обоих изначальных множествах.
• Разность выводит список элементов, которые есть в одном множестве, но отсутствуют в другом.
• Подмножество выдает булево значение, которое показывает, включает ли одно множество все элементы другого множества.

Упражнения от freeCodeCamp

• Create a Set Class
• Remove from a Set
• Size of the Set
• Perform a Union on Two Sets
• Perform an Intersection on Two Sets of Data
• Perform a Difference on Two Sets of Data
• Perform a Subset Check on Two Sets of Data
• Create and Add to Sets in ES6
• Remove items from a set in ES6
• Use .has and .size on an ES6 Set
• Use Spread and Notes for ES5 Set() Integration

Map

Map — это структура, которая хранит данные в парах ключ/значение, где каждый ключ уникален. Иногда её также называют ассоциативным массивом или словарём. Map часто используют для быстрого поиска данных. Она позволяет делать следующие вещи:

• добавлять пары в коллекцию;
• удалять пары из коллекции;
• изменять существующей пары;
• искать значение, связанное с определенным ключом.

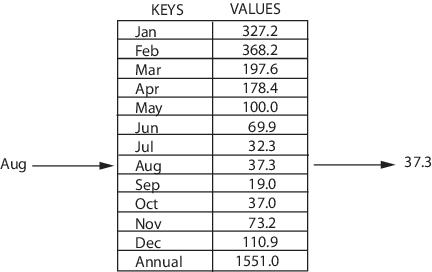
Так устроена структура map

Источник

Полное бинарное дерево. Куча. Очередь с приоритетом

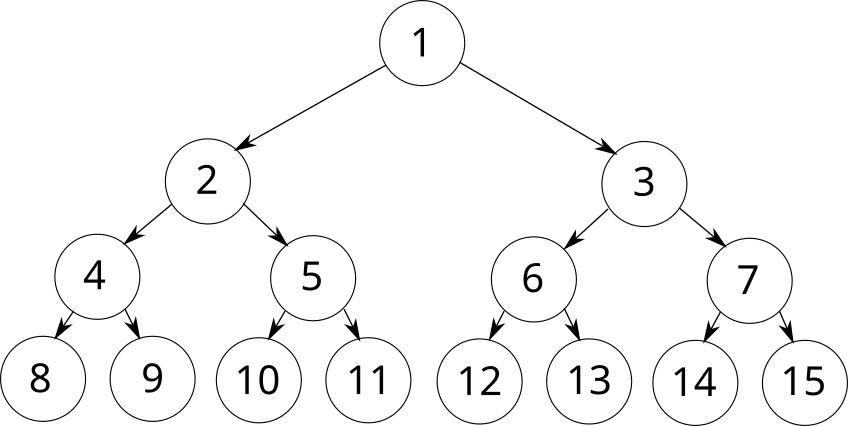
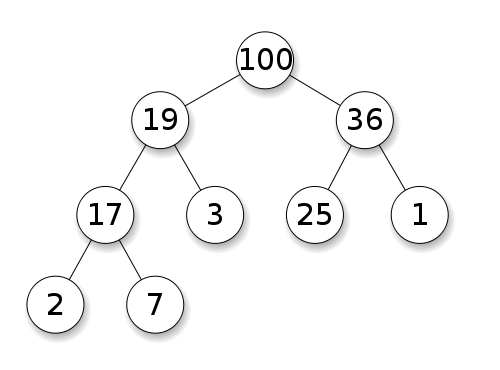
Среди деревьев выделяют особый подкласс, называемый бинарными деревьями. Бинарное дерево — корневое дерево, каждая вершина которого имеет не более двух дочерних, чаще всего чётко упорядоченных: левую и правую. Например, это дерево является бинарным:

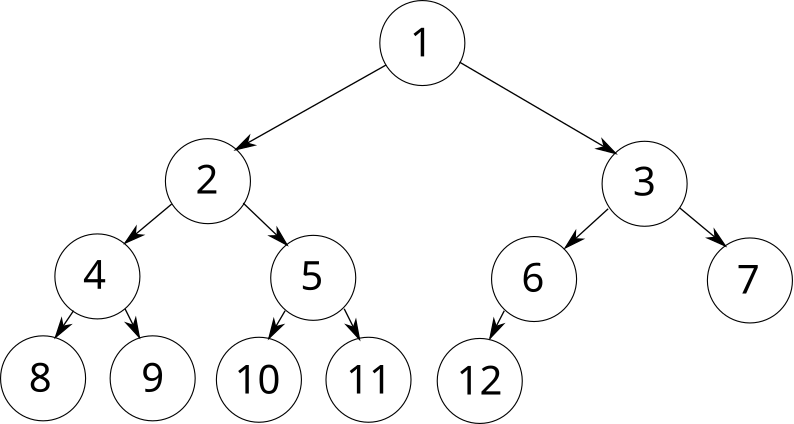
Среди бинарных деревьев отдельно выделяют полные бинарные деревья, все вершины которых имеют по две дочерних, кроме листьев, которые расположены на одинаковой глубине:

Также полными часто называют бинарные деревья, у которых полностью заполнены все уровни, кроме последнего:

При 1-индексации вершин по уровням, приведённой выше, существуют простые формулы перехода между вершинами. Для вершины с индексом \(v\) формулы для спуска влево, спуска вправо, и подъёма вверх выглядят следующим образом:

\[l = 2v \\ r = 2v + 1 \\ p = \left\lfloor \right\rfloor\]

В связи с этим полные бинарные деревья чаще всего хранят не в виде списка смежности, а в виде простого массива, где \(tree[v]\) — некоторое значение, присвоенное вершине с индексом \(v\). Для обхода дерева используются формулы, приведённые выше.

Стоит отметить, что высота (количество уровней) полного бинарного дерева из \(N\) вершин равна \(\log N\). Это свойство часто используется для оценки сложности различных алгоритмов.

Куча

Куча (англ. heap) — одна из простейших структур данных, основанных на деревьях. Куча используется для поддерживания некоторого множества элементов с возможностью быстрого нахождения максимума (или минимума, это не принципиально).

Классическая куча поддерживает следующие операции:

• Добавить элемент (Сложность: \(O(\log N)\))
• Найти максимум (Сложность: \(O(1)\))
• Извлечь максимальный элемент (Сложность: \(O(\log N)\))

Элементы в куче хранятся в виде полного бинарного дерева. Главное его свойство (инвариант кучи) формулируется следующим образом:

Элемент в каждой вершине больше либо равен элементов во всех дочерних вершинах.

Из этого свойства следует, что минимальный элемент всегда будет находиться в корне дерева.

При добавлении в кучу нового элемента, ему присваивается первый доступный индекс. То есть, бинарное дерево заполняется по уровням слева направо. После добавления элемента возможно, что инвариант кучи перестанет выполняться, так как новый элемент будет больше своего прямого предка. В таких случаях просто меняем элемент местами с прямым предком. Если инвариант кучи всё ещё не выполняется, меняем его местами с новым предком, и так далее, пока куча не нормализуется. Такая операция называется проталкиванием вверх.

При извлечении максимального элемента воспользуемся следующей хитростью: переместим последний элемент в куче (крайний правый на последнем уровне) в корень дерева на место удалённого максимума. Это почти наверняка нарушит инвариант, так как новый “максимум” будет меньше элементов в дочерних вершинах. Сравним два дочерних элемента, выберем из них больший, и поменяем его местами с текущим “максимумом”. Повторяем эту операцию, пока инвариант не восстановится. Это называется проталкиванием вниз.

Реализация

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69
 
struct heap  vectorint> tree; heap()  tree.push_back(0); //Мы собираемся работать в 1-индексации, поэтому //просто поместим в tree[0] произвольное значение. > void push(int x)  tree.push_back(x); sift_up(tree.size() - 1); > int max()  if (tree.size() > 1)  return tree[1]; > else  //Ошибка: попытка найти максимум в пустой куче > > void pop()  if (tree.size() > 1)  tree[1] = tree.back(); tree.pop_back(); sift_down(1); > else  //Ошибка: попытка извлечь максимум из пустой кучи > > //Проталкивание вверх. void sift_up(int v)  if (v == 1)  return; //Больше некуда подниматься. > if (tree[v / 2]  tree[v])  swap(tree[v], tree[v / 2]); sift_up(v / 2); > > //Проталкивание вниз void sift_down(int v)  if (v * 2 >= tree.size())  return; //Больше некуда спускаться. > //Индекс большего дочернего элемента int max_idx; if (v * 2 + 1 == tree.size())  //Если можно спуститься только влево max_idx = v * 2; > else if (tree[v * 2] >= tree[v * 2 + 1])  max_idx = v * 2; > else  max_idx = v * 2 + 1; > if (tree[v]  tree[max_idx])  swap(tree[v], tree[max_idx]); sift_down(max_idx); > > bool empty()  return tree.size() == 1; > >; 
 
Понятие очереди с приоритетом
 
Вы можете услышать, как вместо термина “куча” используется термин “очередь с приоритетом”. На практике они взаимозаменимы, хотя разница в значении всё-таки присутствует.
 
Очередь с приоритетом - абстракная структура данных, позволяющая поддерживать множество элементов, находить и извлекать минимум из него, тогда как куча - конкретная структура данных, основанная на полном бинарном дереве. Любая куча является очередью с приоритетом, но не любая очередь с приоритетом (в теории) является кучей (на практике почти что любая). Вы можете реализовать поддержку множества с извлечением максимума с помощью простого массива, она будет иметь сложность операций \(O(N)\), но всё равно являться очередью с приоритетом.
 
(Если вы знакомы с объектно-ориентированным программированием, то очередь с приоритетом - интерфейс, а куча - класс, реализующий его.)
 
Очередь с приоритетом в стандартной библиотеке C++
 
В стандартной библиотеке C++ присутствует реализация кучи, поддерживающая все операции, приведённые выше. Это класс std::priority_queue . Для работы с ним используются следующие методы:
 
bool empty(); unsigned int size(); T top(); //"Верхний" элемент. По умолчанию - максимум. void push(T x); //Добавить элемент в очередь. void pop(); //Извлечь элемент. 
 
По умолчанию используется куча для поиска максимума. Для использования кучи для поиска минимума нужно использовать тип std::priority_queue, greater> .
 
brestprog
 
Олимпиадное программирование в Бресте и Беларуси
 
Источник