Главная » Деревья

Стягивающее дерево неориентированного графа

Содержание
  1. АЛГОРИТМЫ ПОИСКА ОСТОВА ГРАФА. Понятия и определения
  2. 1.4.Стягивающие деревья (каркасы)
  3. 58. Стягивающие деревья. Нахождение стягивающего дерева методом поиска в ширину
  4. 59. Стягивающие деревья. Нахождение стягивающего дерева методом поиска в глубину.
  5. 60.Минимальные покрывающие деревья. Алгоритм Прима
  6. 61.Минимальные покрывающие деревья. Алгоритм Крускала.

АЛГОРИТМЫ ПОИСКА ОСТОВА ГРАФА. Понятия и определения

Деревом называется произвольный неориентированный связный граф без циклов. Для произвольного связного неориентированного графа G = á V, Е ñ каждое деревоá V, Т ñ, где Т Í Е, будем называть остовом или стягивающим деревом графа G. Ребра такого дерева будем называть ветвями, а все остальные ребра графа будем называть хордами.

Отметим, что каждое дерево с n вершинами имеет n -1 ребер.

Использование алгоритма поиска в глубину

Процедуры поиска в глубину и в ширину можно простым способом использовать для нахождения стягивающих деревьев. В обоих случаях достижение новой вершины u из вершины v вызывает включение в дерево ребра < v, u >.

Алгоритм 4.1. Нахождение стягивающего дерева связного графа методом поиска в глубину.

Исходные данные: Связный граф G = á V, Е ñ, заданный соответствиями G [ v ], v Î V.

Результаты: Стягивающее дерево á V, Т ñ графа G.

procedure WGD (v);

(*прохождение в глубину и нахождение ребер дерева; переменные new, G, Т — глобальные *)

new [ v ]:= ложь;

for u Î G [ v ] do

if new [ u ] then (* < v, u > — новая ветвь *) begin

T:= T È < v, u >; WGD (u)

end; (* WGD *)

begin (* главная программа *)

for u Î V do new [ u ]:= истина; (*инициализация*)

T:=Æ; (* Т = множество найденных к этому моменту ветвей *)

WGD (r) (* r — произвольная вершина графа*)

Вычислительная сложность алгоритма есть, очевидно, O (n+m), т.е. того же порядка, что и при поиске в глубину. Пример стягивающего дерева, построенного алгоритмом 4.1, приведен на рис. 4.1,а. Ветви дерева выделены жирными линиями.

Рис. 4.1. Стягивающие деревья, построенные с помощью алгоритма 4.1 (а) и алгоритма 4.2 (б).

Использование алгоритма обхода в ширину

Подобным же способом можно построить стягивающее дерево, используя метод поиска в ширину.

Алгоритм 4.2. Нахождение стягивающего дерева связного графа методом поиска в ширину.

Исходные данные: Связный граф G= á V, Е ñ, представленный соответствиями G [ v ], v Î V.

Результаты: Стягивающее деревоá V, Т ñ графа G

for u Î V do new [ u ]:= истина; (* инициализация *)

T:=Æ; (* T -множество найденных к этому моменту ветвей*)

ОЧЕРЕДЬ = Æ; ОЧЕРЕДЬ Ü r;

Читайте также:  Синие отметки на деревьях

new [ r ]:= ложь; (* r -корень стягивающего дерева *)

while ОЧЕРЕДЬ ¹ Æ do begin

v Ü ОЧЕРЕДЬ;

for u Î G [ v ] do

if new [ u ] then (* < v, u > = новая ветвь*) begin

ОЧЕРЕДЬ Ü u;

new [ u ]:= ложь;

Данный алгоритм строит стягивающее дерево для неориентированного связного графа за O (m+n) шагов.

На рис. 4.1, б дан пример стягивающего дерева, построенного алгоритмом 4.2. Ветви его выделены на графе жирными линиями.

Изложенные результаты легко переносятся и на произвольные графы, не обязательно связные. Максимальный суграф без циклов произвольного графа G называется стягивающим лесом графа G, Очевидно, что стягивающий лес графа с k компонентами связности определяется через стягивающие деревья этих компонент и, следовательно, содержит n — k -1 ребер.

4.4. Лабораторная работа №4: “Поиск остова графа”

Цель работы:

Исследовать свойства достижимости и связности вершин в неориентированном графе, используя алгоритмы поиска стягивающего дерева в графе.

Используя методические указания раздела 4 разработать исследовательскую программу поиска остовного дерева или леса в неориентированном графе от заданной вершины, используя один из алгоритмов поиска по выбранному варианту.

Варианты выполнения работы:

1) Использование рекурсивного алгоритма поиска в графе в глубину;

2) Использование нерекурсивного алгоритма поиска в графе в глубину;

3) Использование алгоритма поиска в графе в графе в ширину.

Порядок выполнения работы

Работа рассчитана на 2 часа. Составленная в результате исследовательская программа должна находить в заданном неориентированном графе следующие элементы:

· список вершин каждого остовного дерева в порядке его прохождения;

· список ребер в каждом остовном дереве.

В качестве тестов для отладки программы и решения исследовательских задач рекомендуем использовать следующие графы:

1) Связный неориентированный граф из 9 вершин, представленный на рис. 4.1.

2) Неориентированный граф с числом вершин не менее 12, состоящий из трех связных компонент. Этот граф выбрать самостоятельно.

Источник

1.4.Стягивающие деревья (каркасы)

Деревом называется произвольный неориентированный связный граф без циклов. Для произвольного связного неориентированного графа G = каждое дерево , где , будем назвать стягивающим деревом (каркасом или остовом) графа G. Ребра такого дерева являются ветвями, а все остальные ребра графа – хордами (очевидно это имеет смысл в контексте фиксированного стягивающего дерева). Следует отметить, что каждое дерево с n вершинами имеет n-1 ребер. Этот факт можно просто доказать, применяя индукцию относительно n.

Процедуры поиска в глубину и в ширину можно простым способом использовать для нахождения стягивающих деревьев. В обоих случаях достижение новой вершины u из вершины v вызывает включение в дерево ребра .

Читайте также:  Кресло с подушками дерево

WGD = proc (v:int; g:graph; НОВЫЙ:array of bool; T:stack)

modifies НОВЫЙ, T

effects 1. НОВЫЙ [v] = false

2. c = graph.fetch(g,v); i = circ.size(c)

3. пока i > 0

3.2. если НОВЫЙ[j], то

3.2.1. stack.pop(T,v); stack.pop(T,j)

3.2.2. WGD(j,g,НОВЫЙ,T)

иначе circ.change(c)

Рис.1.14.Процедура поиска в глубину в сочетании с нахождением ребра дерева.

Frame1 = proc(g:graph; r:int) returns(T:stack)

effects 1. для i = 1 до n НОВЫЙ[i] = true

3. WGD(r,g,НОВЫЙ,T)

Рис.1.15.Процедура нахождения стягивающего дерева связного графа методом поиска в глубину.

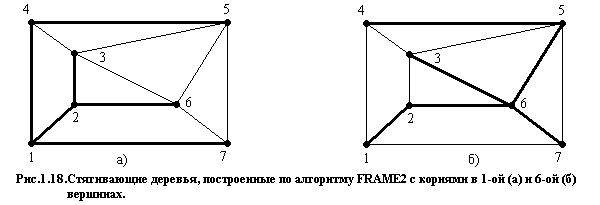
На рис.1.16 представлены результаты определения стягивающих деревьев для графа, представленного на рис.1.1.б в общем виде и на рис.1.5.а в виде «массива» кольцевых структур, начиная от 1-ой (рис.1.16.а) и 6-ой вершин (рис.1.16.б).

Каждое стягивающее дерево, построенное алгоритмом Frame1, обладает следующим свойством. Назовем вершину r, с которой начинается поиск в графе, корнем стягивающего дерева . Очевидно, что в дереве существует только один путь от произвольной вершины к корню.

Для двух различных вершин v и u дерева будем считать, что u является потомком вершины v, если v лежит на пути (в дереве ) из u в корень. Если при этом имеет место v-u, то u – сын вершины v, v – отец вершины u.

Подобным способом можно построить стягивающее дерево, используя метод поиска в ширину.

Frame2 = proc (g:graph; r:int) returns (T:stack)

effects 1. для i = 1 до n НОВЫЙ[i] = true

5. НОВЫЙ[r] = false

6. пока not(intqueue.isempty(q))

6.1. v = intqueue.remfirst(q)

6.2. c = graph.fetch(g,v); i = circ.size(c)

6.3. пока i > 0

6.3.2. если НОВЫЙ[u], то

6.3.2.1. intqueue.append(q,u)

6.3.2.2. НОВЫЙ[u] = false

Рис.1.17.Процедура нахождения стягивающего дерева связного графа методом поиска в ширину.

На рис.1.18 представлены результаты определения стягивающих деревьев для графа, представленного на рис.1.1.б в общем виде и на рис.1.5.а в виде «массива» кольцевых структур, начиная от 1-ой (рис.1.18.а) и 6-ой вершин (рис.1.18.б).

Построение стягивающего дерева с помощью процедуры Frame2 обеспечивает следующее свойство. Пусть — стягивающее дерево связного графа , построенное при помощи Frame2. Тогда путь в из произвольной вершины v до корня r является к ратчайшим путем из v в r в графе G.

Источник

58. Стягивающие деревья. Нахождение стягивающего дерева методом поиска в ширину

Для про­извольного неориентированного графа G = каждое дерево , где ТсЕ, будем называть стягиваю­щим деревом или каркасом графа G. Ребра такого графа (дерева) назовем ветвями, а остальные ребра графа G будем называть хордами.

Поиск в ширину. О(n+m)

2.FOR uV DO НОВЫЙ[u] := true;

3.T :=;

Читайте также:  Бархатное дерево польза ягод

4.ОЧЕРЕДЬ := ; ОЧЕРЕДЬ  r;

6.WHILE ОЧЕРЕДЬ DO BEGIN

8.FOR u СПИСОК[u] DO

10.ОЧЕРЕДЬ и; НОВЫЙ[u] := false; Т := Т

59. Стягивающие деревья. Нахождение стягивающего дерева методом поиска в глубину.

Для про­извольного неориентированного графа G = каждое дерево , где ТсЕ, будем называть стягиваю­щим деревом или каркасом графа G. Ребра такого графа (дерева) назовем ветвями, а остальные ребра графа G будем называть хордами.

В глубину. С(n+m)

исходный граф G = задан списками инцидентности.

1. For each v do Mark[v]

2.T 3.dfst(v0)

2.for each wV, смеж. С v do

4.TT

60.Минимальные покрывающие деревья. Алгоритм Прима

Остовным(покрывающим) деревом называется подграф, не содержащий циклов, включающий все вершины исходного графа, для которого сумма весов ребер минимальна. Минимальное остовное дерево в связанном, взвешенном, неориентированном графе — это остовное дерево этого графа, имеющее минимальный возможный вес, где под весом дерева понимается сумма весов входящих в него рёбер. В методе Прима от исходного графа переходим к его представлению в виде матрицы смежности. На графе выбирается произвольная вершина. Выбранная вершина образует первоначальный фрагмент остовного дерева. Затем анализируются веса ребер от выбранной вершины до оставшихся невыбранных вершин. Выбирается минимальное ребро, которое указывает на следующую выбранную вершину, и т.д. процесс продолжается до тех пор, пока в остновное дерево не будут включены все вершины исходного графа.

Алгоритм Prim(G,T)

1.T ; w ;

2.while wv do

3.среди ребер, соед. W и V-W найти ребро (w,v) с наименьшим весом; 4.TT;5.WV;

61.Минимальные покрывающие деревья. Алгоритм Крускала.

Остовным (покрывающим) деревом называется подграф, не содержащий циклов, включающий все вершины исходного графа, для которого сумма весов ребер минимальна. Минимальное остовное дерево в связанном, взвешенном, неориентированном графе — это остовное дерево этого графа, имеющее минимальный возможный вес, где под весом дерева понимается сумма весов входящих в него рёбер. 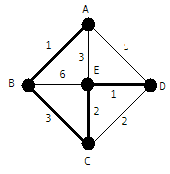Алгоритм Крускала. Вычислительная сложность: Сортировка(mlogn), Основная часть(n 2 ). Первоначально каждая вершина(v1,v2…) исходного графа помещается в одноэлементное множество, где все вершины изолированы (поэтому считается что множество W­s­ имеет вид: Ws=1>,2>,…,n>>. Ребра сортируются по возрастанию. Ребро включается в остовное дерево, если оно связывает вершины, принадлежащие разным множествам. Алгоритм заканчивает работу, когда все вершины объединяются в одно множество, при этом оставшиеся ребра не включаются в оставное дерево. E-количества ребер,V-вершин.

Алгоритм Kruskal(G)

1.for each v­iV do Mark[vi]I;

2.T; LESort[E];

5.if Mark[v]Mark[w] then

6.TT;

8.for each uV do

Источник

Оцените статью
© 2024 Деревья и растения