- 58. Стягивающие деревья. Нахождение стягивающего дерева методом поиска в ширину
- 59. Стягивающие деревья. Нахождение стягивающего дерева методом поиска в глубину.
- 60.Минимальные покрывающие деревья. Алгоритм Прима
- 61.Минимальные покрывающие деревья. Алгоритм Крускала.
- 1.4.Стягивающие деревья (каркасы)
- Каркасы графа. Алгоритм построения остовного дерева методом поиска в глубину
58. Стягивающие деревья. Нахождение стягивающего дерева методом поиска в ширину
Для произвольного неориентированного графа G = каждое дерево , где ТсЕ, будем называть стягивающим деревом или каркасом графа G. Ребра такого графа (дерева) назовем ветвями, а остальные ребра графа G будем называть хордами.
Поиск в ширину. О(n+m)
2

3.T :=;
4.ОЧЕРЕДЬ := ; ОЧЕРЕДЬ r;
6.WHILE ОЧЕРЕДЬ DO BEGIN
8.FOR u СПИСОК[u] DO
10.ОЧЕРЕДЬ и; НОВЫЙ[u] := false; Т := Т
59. Стягивающие деревья. Нахождение стягивающего дерева методом поиска в глубину.
Для произвольного неориентированного графа G = каждое дерево , где ТсЕ, будем называть стягивающим деревом или каркасом графа G. Ребра такого графа (дерева) назовем ветвями, а остальные ребра графа G будем называть хордами.
В глубину. С(n+m)
исходный граф G = задан списками инцидентности.
1. For each v do Mark[v]
2.T 3.dfst(v0)
2.for each wV, смеж. С v do
4.TT
60.Минимальные покрывающие деревья. Алгоритм Прима
Остовным(покрывающим) деревом называется подграф, не содержащий циклов, включающий все вершины исходного графа, для которого сумма весов ребер минимальна. Минимальное остовное дерево в связанном, взвешенном, неориентированном графе — это остовное дерево этого графа, имеющее минимальный возможный вес, где под весом дерева понимается сумма весов входящих в него рёбер. 
Алгоритм Prim(G,T)
1.T ; w ;
2.while wv do
3.среди ребер, соед. W и V-W найти ребро (w,v) с наименьшим весом; 4.TT


61.Минимальные покрывающие деревья. Алгоритм Крускала.
Остовным (покрывающим) деревом называется подграф, не содержащий циклов, включающий все вершины исходного графа, для которого сумма весов ребер минимальна. Минимальное остовное дерево в связанном, взвешенном, неориентированном графе — это остовное дерево этого графа, имеющее минимальный возможный вес, где под весом дерева понимается сумма весов входящих в него рёбер. 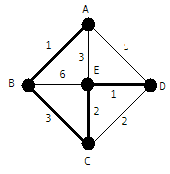

Алгоритм Kruskal(G)
1.for each viV do Mark[vi]I;
2.T; LESort[E];
5.if Mark[v]Mark[w] then
6.TT;
8.for each uV do
Источник
1.4.Стягивающие деревья (каркасы)
Деревом называется произвольный неориентированный связный граф без циклов. Для произвольного связного неориентированного графа G = каждое дерево , где , будем назвать стягивающим деревом (каркасом или остовом) графа G. Ребра такого дерева являются ветвями, а все остальные ребра графа – хордами (очевидно это имеет смысл в контексте фиксированного стягивающего дерева). Следует отметить, что каждое дерево с n вершинами имеет n-1 ребер. Этот факт можно просто доказать, применяя индукцию относительно n.
Процедуры поиска в глубину и в ширину можно простым способом использовать для нахождения стягивающих деревьев. В обоих случаях достижение новой вершины u из вершины v вызывает включение в дерево ребра .
WGD = proc (v:int; g:graph; НОВЫЙ:array of bool; T:stack)
modifies НОВЫЙ, T
effects 1. НОВЫЙ [v] = false
2. c = graph.fetch(g,v); i = circ.size(c)
3. пока i > 0
3.2. если НОВЫЙ[j], то
3.2.1. stack.pop(T,v); stack.pop(T,j)
3.2.2. WGD(j,g,НОВЫЙ,T)
иначе circ.change(c)
Рис.1.14.Процедура поиска в глубину в сочетании с нахождением ребра дерева.
Frame1 = proc(g:graph; r:int) returns(T:stack)
effects 1. для i = 1 до n НОВЫЙ[i] = true
3. WGD(r,g,НОВЫЙ,T)
Рис.1.15.Процедура нахождения стягивающего дерева связного графа методом поиска в глубину.
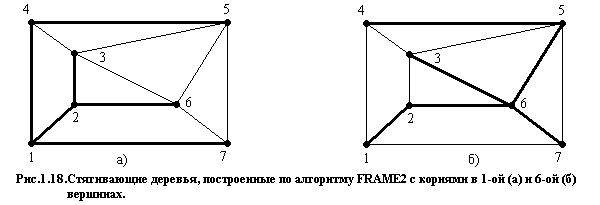
На рис.1.16 представлены результаты определения стягивающих деревьев для графа, представленного на рис.1.1.б в общем виде и на рис.1.5.а в виде «массива» кольцевых структур, начиная от 1-ой (рис.1.16.а) и 6-ой вершин (рис.1.16.б).
Каждое стягивающее дерево, построенное алгоритмом Frame1, обладает следующим свойством. Назовем вершину r, с которой начинается поиск в графе, корнем стягивающего дерева . Очевидно, что в дереве существует только один путь от произвольной вершины к корню.
Для двух различных вершин v и u дерева будем считать, что u является потомком вершины v, если v лежит на пути (в дереве ) из u в корень. Если при этом имеет место v-u, то u – сын вершины v, v – отец вершины u.
Подобным способом можно построить стягивающее дерево, используя метод поиска в ширину.
Frame2 = proc (g:graph; r:int) returns (T:stack)
effects 1. для i = 1 до n НОВЫЙ[i] = true
5. НОВЫЙ[r] = false
6. пока not(intqueue.isempty(q))
6.1. v = intqueue.remfirst(q)
6.2. c = graph.fetch(g,v); i = circ.size(c)
6.3. пока i > 0
6.3.2. если НОВЫЙ[u], то
6.3.2.1. intqueue.append(q,u)
6.3.2.2. НОВЫЙ[u] = false
Рис.1.17.Процедура нахождения стягивающего дерева связного графа методом поиска в ширину.
На рис.1.18 представлены результаты определения стягивающих деревьев для графа, представленного на рис.1.1.б в общем виде и на рис.1.5.а в виде «массива» кольцевых структур, начиная от 1-ой (рис.1.18.а) и 6-ой вершин (рис.1.18.б).
Построение стягивающего дерева с помощью процедуры Frame2 обеспечивает следующее свойство. Пусть — стягивающее дерево связного графа , построенное при помощи Frame2. Тогда путь в из произвольной вершины v до корня r является к ратчайшим путем из v в r в графе G.
Источник
Каркасы графа. Алгоритм построения остовного дерева методом поиска в глубину
Каркас графа Лекция 3 Каркасы графа Каждый граф имеет каркас. Более того, у одного графа может быть несколько каркасов. Связный неориентированный граф называется деревом, если он не имеет циклов. Дерево не имеет петель и кратных ребер Остовное дерево или каркас графа — подграф: 1) содержит все вершины графа, 2) является деревом. Каркасы графа Каркас графа так же называют «Стягивающее дерево» или «Остовное дерево» Ребра графа, вошедшие в каркас будут называться ветвями, а не вошедшие в каркас- хордами. Каркасы можно строить как поиском в глубину, так и поиском в ширину. В любом случае достижение «новой» вершины u из «старой» вершины v означает включение ребра в каркас. Алгоритм построения остовного дерева методом поиска в глубину 1 procedure КАРКАС ГЛУБИНА(v) <поиск в глубину из вершины v, соединенный с нахождением ребра дерева; переменные НОВЫЙ, ЗАПИСЬ, T – глобальные>2 begin НОВЫЙ[v]:= ложь; 3 for u ЗАПИСЬ[v] do 4 if НОВЫЙ[u] then < (u, v) - новая ветвь>5 begin T := T + (v, u); КАРКАС ГЛУБИНА(u) end 6 end ; begin главная программа for u ∈ V do НОВЫЙ[u]:= истина; < инициализация>T := пусто; КАРКАС ГЛУБИНА(r) end. Докажем корректность этого алгоритма. Алгоритм строит СВЯЗНЫЙ граф, т.к. каждое новое ребро (v-u) продолжает уже существующий путь от к к v. Построенный граф не содержит ЦИКЛОВ. Каждая новая ветвь (v-u) соединяет уже рассмотренную v с НОВОЙ и. Чтобы замкнуть, цикл, требуется ребро, соединяющее две уже РАССМОТРЕННЫЕ вершины. Построенный граф содержит ВСЕ вершины графа G — это свойство поиска в глубину. По этой же причине вычислительная сложность алгоритма O(n+m). Свойства каркаса Любой каркас обладает важным свойством — от корня к до произвольной вершины v существует ровно ОДИН путь, состоящий из ветвей каркаса. Если бы их было два, получился» бы цикл, если бы ни одного, каркас не был бы связным. 2. Кроме того, если каркас D построен поиском в-глубину, то для двух вершин u и v, СОЕДИНЕННЫХ РЕБРОМ, всегда можно сказать: или v — потомок и, или и — потомок v (относительно каркаса D). Первое означает, что и лежит на пути из корня к в вершину v, второе — v на пути из к в и. Это легко доказать. Пусть одна из вершин, например,v просмотрена раньше и. Построен путь от корня к до v. Процесс поиска в глубину начинается с вершины v. Taк как и u v соединены ребром, то, рано или поздно, будет рассмотрена вершина u и построен путь от v до u. Получился путь k—v—u. Если v и и соединены ВЕТВЬЮ каркаса, то одна из них— СЫН, другая — ОТЕЦ. 1. Алгоритм построения остовного дерева методом поиска в ширину Данные: связный граф G= . представленный списками ЗАПИСЬ[v], v e V. Результаты: каркас D = графа G. •begin for u Запись[V] do НОВЫЙ[u] :=истина; •T:=0 •ОЧЕРЕДЬ=NIL; ОЧЕРЕДЬ NIL do 7 begin v 1 выполнить: 6. < выбрать в Q ребро (v, w) наименьшей стоимости; 7. удалить (v, w) из Q; 8. если v и w принадлежат различным множествам W1 и W2 из VS то 9. < заменить W1 и W2 на W1W2 в VS; 10. добавить (v, w) к Т; >> Пример 23 4 1 9 3 17 Время работы: Cортировка рёбер — O(|E|×log|E|) Компоненты связности удобно хранить в виде системы непересекающихся множеств. Все операции в таком случае займут O(E) Получившееся дерево является каркасом минимального веса. Введем массив меток вершин графа Mark. Начальные значения элементов массива равны номерам соответствующих вершин (Mark[i] = i; i 1.. N). Ребро выбирается в каркас в том случае, если вершины, соединяемые им, имеют разные значения меток. Пример приведен на следующем слайде, изменения Mark показаны в таблице. Алгоритм Краскала с системой непересекающихся множеств Так же, как и в простой версии алгоритма Крускала, отсортируем все рёбра по неубыванию веса. Затем поместим каждую вершину в своё дерево (т.е. в своё множество) с помощью вызова функции MakeSet — на это уйдёт в сумме O (N). Перебираем все рёбра и для каждого ребра за O (1) определяем, принадлежат ли его концы разным деревьям (с помощью двух вызовов FindSet за O (1)). Наконец, объединение двух деревьев будет осуществляться вызовом Union — также за O (1). Итого мы получаем: O (M log N + N + M) = O (M log N). Реализация за O (M log N + N2) Отсортируем все рёбра в списках смежности каждой вершины по увеличению веса – O (M log N)). Для каждой вершины заведем указатель, указывающий на первое доступное ребро в её списке смежности. Изначально все указатели указывают на начала списков. На i-ой итерации перебираем все вершины, и выбираем наименьшее по весу ребро среди доступных. Поскольку всё рёбра уже отсортированы по весу, а указатели указывают на первые доступные рёбра, то выбор наименьшего ребра осуществится за O (N). После этого обновляем указатели (сдвигаем вправо), т.к. некоторые из них указывают на ставшие недоступными рёбра (оба конца которых оказались внутри дерева). На поддержание работы указателей требуется O (M) действий. Количество остовных деревьев графа • Количество остовных деревьев(каркасов) графа определяется матрицей Кирхгофа , а именно: алгебраическим дополнением любого элемента матрицы Кирхгофа. Матрица Кирхгофа • Матрица (n*n) • По диагонали – степени вершин • остальные элементы (i,j) при наличии ребра заполняются -1 1 2 3 4 1 1 -1 2 -1 3 -1 -1 3 -1 2 -1 4 -1 -1 2
Источник