Свободные группы и деревья

Глава 9 Деревья

Деревья заслуживают отдельного и подробного рассмотрения по двум причинам.

• Деревья являются в некотором смысле простейшим классом графов. Для них выполняются многие свойства, которые не всегда выполняются для графов в общем случае. Применительно к деревьям многие доказательства и рассужде­ния оказываются намного проще. Выдвигая какие-то гипотезы при решении задач теории графов, целесообразно сначала их проверять на деревьях.
• Деревья являются самым распространенным классом графов, применяемых в программировании, причем в самых разных ситуациях. Более половины объ­ема этой главы посвящено рассмотрению конкретных применений деревьев в программировании.

9.1. Свободные деревья

9.1.1. Определения

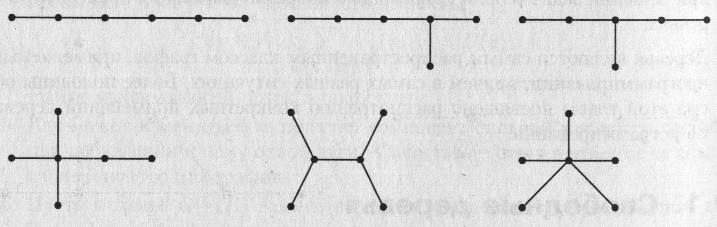
Граф без циклов называется ациклическим, или лесом. Связный ациклический граф называется (свободным) деревом. Таким образом, компонентами связности леса являются деревья. ЗАМЕЧАНИЕ Прилагательное «свободное» употребляется в том случае, когда нужно подчеркнуть от­личие деревьев от других объектов, родственных деревьям: ориентированных деревьев, упорядоченных деревьев и т. д. В связном графе G выполняется неравенство q(G)  p(G) — 1. Граф G, в котором q(G)=p(G)-1, называется древовидным. В ациклическом графе G z(G) = 0. Пусть u, v — несмежные вершины графа G, х = (u, v)  Е. Если граф G + х имеет только один простой цикл, z(G + х) = 1, то граф G называется субциклическим. Пример На рис. 9.1 показаны диаграммы всех различных (свободных) деревьев с 5 вер­шинами, а на рис. 9.2 — диаграммы всех различных (свободных) деревьев с 6 вершинами Рис. 9.1. Свободные деревья с 5 вершинами Рис. 9.2. Свободные деревья с 6 вершинами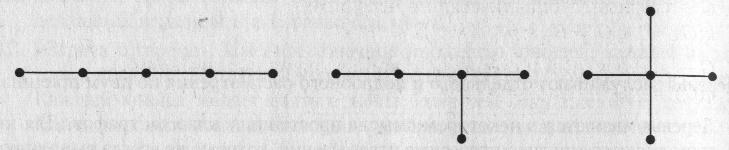

9.1 .2. Основные свойства деревьев

Следующая теорема устанавливает, что два из четырех свойств — связность, аци­кличность, древовидность и субцикличность — характеризуют граф как дерево. ТЕОРЕМА Пусть G(V, Е) — граф с р вершинами, q ребрами, k компонентами связности и z простыми циклами. Пусть далее х — ребро, соединяющее любую пару несмежных вершин в G. Тогда следующие утверждения эквивалентны: 1. G — дерево, то есть связный граф без циклов, k(G)=1&z(G)=0; 2. любые две вершины соединены в G единственной простой цепью, u, v  ! ; 3. G — связный граф, и любое ребро есть мост, k(G) = l&eЕ k(G – е) > 1;. 4. G — связный и древовидный, k(G) = l&q(G)=p(G)-l; 5. G — ациклический и древовидный, z(G) = 0&q(G)=p(G)-l; 6. G — ациклический и субциклический, z(G) =0&z(G + x) = 1; 7. G — связный, субциклический и неполный, k(G) = l&GK_p&p3&z(G + x) = 1; 8. G — древовидный и субциклический (за двумя исключениями), q(G)=p(G)-l&GK₁K₃&GK₂K₃&z(G + x) = l. доказательство [1 2.] От противного. Пусть существуют две цепи (рис. 9.3 слева). Тогда w₁, w₂ — простой цикл. Рис. 9.3. К доказательству теоремы о свойствах деревьев [2 3.] Имеем: u,v ! , следовательно, k(G) = 1. Далее от противного. Пусть ребро х — не мост. Тогда в G — х концы этого ребра связаны цепью. Само ребро х — вторая цепь. [3 4.] Индукция по p. База: р=1  q = 0. Пусть q(G) = p(G) —1 для всех графов G с числом вершин меньше р, у которых любое ребро суть мост. Тогда удалим из G ребро х (которое является мостом). Получим две компоненты G’ и G», удовлетворяющие индукционному предположению. Имеем: q’ = р’ — 1, q» = р» — 1, q = q’ + q» + 1 = р’ — 1 + р» — 1 + 1 = р — 1. [4 5.] От противного. Пусть есть цикл с n вершинами и n ребрами. Остальные р — n вершин имеют инцидентные им ребра, которые связывают их с циклом. Следовательно, q  р, что противоречит условию q = р — 1. [51.] Граф без циклов, следовательно, его компоненты — деревья. Пусть их k. Имеем: Ho q = p — 1, следовательно, k = 1. [56.] По ранее доказанному 5  1 2. Имеем: u,v ! . Соединив две несмежные вершины, получим единственный простой цикл. [67.] При р  3 граф К_р содержит цикл, следовательно, G  К_р. Далее от противного. Пусть G несвязен, тогда при соединении ребром двух ком­понент связности цикл не возникнет. [72.] Имеем k(G) = 1, следовательно, u,v  . Пусть цепь не единственная. Тогда существует цикл Z, причем Z = К₃ = C₃. Действительно, пусть Z > Сз, тогда, соединив две несмежные вершины этого цикла, получим два цикла. Но G связен и G  K₃, следовательно, существу­ет другая вершина w, смежная с Z = К₃ (см. рис. 9.3 справа). Если w смежна с более чем одной вершиной Z, то имеем больше одного цикла. Если w смежна только с одной вершиной Z, то соединив ее с другой вершиной, получим два цикла. [78.] Имеем k(G) = 1, следовательно, G  К₂  K₃, G  K₁  K₃. Имеем по доказанному: 723 4, то есть q = р — 1. [85.] От противного. Пусть в G есть цикл Z = С_n. Если n > 3, то если внутри Z уже есть смежные вершины, имеем два цикла. Если в Z нет смежных вершин, то, соединив несмежные вершины в Z, получим два цикла. Сле­довательно, Z = К₃. Этот цикл Z является компонентой связности G. Действительно, пусть это не так. Тогда существует вершина w, смежная с Z. Если w смежна более чем с одной вершиной Z, то имеем больше одного цикла. Если w смежна только с одной вершиной Z, то, соеди­нив ее с другой вершиной, получим два цикла. Рассмотрим G’: = G — Z. Имеем: р = р’ + 3, q = q’ + 3. Но q = р — 1, следовательно, q’ = р’ — 1. От­сюда z(G’) = 0, так как один цикл уже есть. Следовательно, компоненты G’ — деревья. Пусть их fc. Имеем: но q’ = p’ — 1, следовательно, k = 1, то есть дерево одно. Если в этом дереве соединить несмежные вершины, то получим второй цикл. Два исключения: деревья, которые не имеют несмежных вершин, — это К₁ и К₂. Общая схема доказательства представлена на рис. 9.4. Граф доказательства силь­но связен, следовательно, теорема доказана. Рис. 9.4. Схема доказательства теоремы о свойствах деревьев СЛЕДСТВИЕ В любом нетривиальном дереве имеются по крайней мере две ви­сячие вершины. доказательство Рассмотрим дерево G(V,E). Дерево — связный граф, следовательно, v_iV d(v_i)1. Далее от противного. Пусть i l..p — l d(v_i) > 1. Тогда . Но q = р — 1, то есть 2q = 2р — 2. Имеем противоречие: 2р — 2 > 2р — 1.

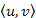
Источник

Свободные деревья

Одним из простейших классом графов являются деревья. Граф является деревом, если он удовлетворяет следующей теореме.

Теорема. Для графа G= следующие утверждения эквивалентны:

2) любые две вершины в графе G соединены единственной простой цепью;

3) граф G связен и имеет |X| — 1 ребер;

4) граф G не содержит циклов и имеет |X| — 1 ребер;

5) граф G не содержит циклов, но добавление ребра между любыми двумя несмежными вершинами приводит к появлению одного цикла;

6) граф G связен, но утрачивает это свойство после удаления любого ребра.

Деревья широко применяются в программировании.

Свободные деревья

Граф без циклов называется ациклическим, или лесом. Связный ациклический граф называется (свободным) деревом. Компонентами связности леса являются деревья.

Граф G, в котором q(G) = р(G)- 1, называется древовидным.

В ациклическом графе G z(G) = 0. Пусть и, v — несмежные вершины графа G, х = (и, v) E. Если граф G+x имеет только один простой цикл, z(G+х)= 1, то граф G называется субциклическим.

На рис. 9.1 показаны диаграммы всех различных (свободных) деревьев с 5 вершинами, а на рис. 9.2 — диаграммы всех различных (свободных) деревьев с 6 вершинами.

Рис. 9.1. Свободные деревья с 5 вершинами

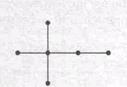
Рис. 9.2. Свободные деревья с 6 вершинами

Основные свойства деревьев

Следующая теорема устанавливает, что два из четырех свойств — связность, ацикличность, древовидность и субцикличность — характеризуют граф как дерево.

Пусть G(V, Е) — граф с р вершинами, q ребрами, k компонентами связности и z простыми циклами. Пусть далее х — ребро, соединяющее любую пару несмежных вершин в G. Тогда следующие утверждения эквивалентны:

1. G — дерево, то есть связный граф без циклов, k(G) = 1&z(G) = 0;

2. любые две вершины соединены в G единственной простой цепью,

Читайте также:  Крайслер 300с салон дерево

3. G — связный граф, и любое ребро есть мост,

4. G — связный и древовидный,

6. G — ациклический и субциклический,

7. G — связный, субциклический и неполный,

8. G — древовидный и субциклический (за двумя исключениями),

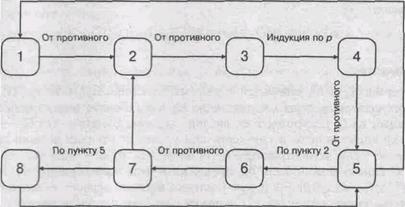
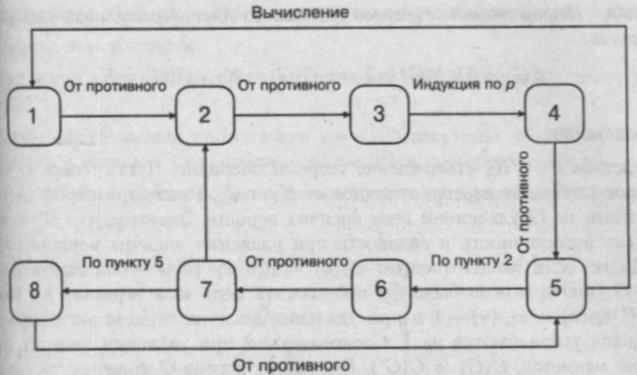
[1 2] От противного. Пусть существуют две цепи ; (рис. 9.3, слева). Тогда w, w₂ — простой цикл.

Рис. 9.3. К доказательству теоремы о свойствах деревьев

[2 3.] Имеем: и, v !, следовательно, . Далее от противного. Пусть ребро х — не мост. Тогда в G — х концы этого ребра связаны цепью. Само ребро х — вторая цепь.

[3 4.] Индукция по р. База: р = 1 q = 0. Пусть для всех связанных графов G с числом вершин меньше р, у которых любое ребро суть мост. Тогда удалим из G ребро х (которое является мостом). Получим две компоненты G ‘ и G ", удовлетворяющие индукционному предположению. Имеем:

[4 5.] От противного. Пусть есть цикл с п вершинами и п ребрами. Остальные р — п вершин имеют инцидентные им рёбра, которые связывают их с циклом, Следовательно, q ≥ р, что противоречит условию q = р — 1.

[5 1.] Граф без циклов, следовательно, его компоненты — деревья. Пусть их k;. Имеем:

Но q=p-1, следовательно, k = 1.

[5 6.] По ранее доказанному 5 1 2. Имеем: . Соединив две несмежные вершины, получим единственный простой цикл.

[6 7.] При р ≥ 3 граф К_р содержит цикл, следовательно, G ≠ К_р. Далее от противного. Пусть G несвязен, тогда при соединении ребром двух компонент связности цикл не возникнет.

[7 2.] Имеем k(G) = 1, следовательно, . Пусть цепь не единственная. Тогда существует цикл Z, причем Z = К₃, = С₃. Действительно, пусть Z > С₃, тогда, соединив две несмежные вершины этого цикла, получим два цикла. Но G связен и G ≠ К₃, следовательно, существует другая вершина w, смежная с Z = К₃ (см. рис. 9.3, справа). Если w смежна более чем с одной вершиной Z, то имеем больше одного цикла. Если w смежна только с одной вершиной Z, то соединив её с другой вершиной, получим два цикла.

Читайте также:  Можно ли протирать прыщи маслом чайного дерева

[7 8.] Имеем k(G) = 1, следовательно, G ≠ К₂ К₃, G ≠ К₁ К₃. Имеем по доказанному: 7 2 3 4, то есть q = р- 1.

[8 5.] От противного. Пусть в G есть цикл Z = С_п. Если n > 3, то если внутри Z уже есть смежные вершины, имеем два цикла. Если в Z нет смежных вершин, то, соединив несмежные вершины в Z, получим два цикла. Следовательно, Z = К₃. Этот цикл Z является компонентой связности G. Действительно, пусть это не так. Тогда существует вершина w, смежная с Z. Если w смежна более чем с одной вершиной Z, то имеем больше одного цикла. Если w смежна только с одной вершиной Z, то, соединив её с другой вершиной, получим два цикла. Рассмотрим G:=G — Z. Имеем: р = р’ + 3, q = q’ + 3. Но q = р — 1, следовательно, q’ = р’ — 1. Отсюда z(С’) = 0, так как один цикл уже есть. Следовательно, компоненты G’ — деревья. Пусть их k. Имеем:

но q’ = p’ -1, следовательно. k = 1. то есть дерево одно. Если в этом дереве сбединить несмежные вершины, то получим второй цикл. Два исключения: деревья, которые не имеют несмежных вершин, — это К₁ и K₂.

Общая схема доказательства представлена на рис. 9.4. Граф доказательства сильно связен, следовательно, теорема доказана.

Рис. 9.4. Схема доказательства теоремы о свойствах деревьев

Следствие 1 В любом нетривиальном дереве имеются по крайней мере две висячие вершины.

Рассмотрим дерево G(V, Е). Дерево — связный граф, следовательно, .

Далее от противного. Пусть . Тогда

2q = Уd(vi) > 2(р — 1) + 1 = 2р — 1.

Но q = р — 1, то есть 2q = 2р — 2. Имеем противоречие: 2р — 2 2 > 2р — 1.

Следствие 2. Каждая не висячая вершина свободного дерева является точкой сочленения.

Пусть G(V, Е) — дерево, v V и d(v) > 1. Тогда и, w V(u,v) E& (u, w) E. Граф G связен, поэтому существует цепь (и, w). Если v ;, то имеем цикл v, , v, что противоречит тому, что G — дерево. Следовательно, и, w V v и по теореме 8.1.2 вершина v — точка сочленения.

Свободные деревья выделяются из других графов тем, что их центр всегда оправдывает своё название.

Центр свободного дерева состоит из одной вершины или из двух смежных вершин:

Z(G) = 0&k(G) = 1 → С(G) = К₁ С(G) = К₂.

Для деревьев К₁ и К₂ утверждение теоремы очевидно. Пусть теперь G(V,Е) — некоторое свободное дерево, отличное от К₁ и К₂. Рассмотрим граф G'(V’,Е’), полученный из G удалением всех висячих вершин. Заметим, что G ‘ — дерево, поскольку ацикличность и связность при удалении висячих вершин сохраняется. Далее, если эксцентриситет е_G(v) = d(v,и), то и — висячая вершина в дереве G (иначе можно было бы продолжить цепь «за» вершину и ). Поэтому v V’ е_G(v) = е_G‘(v)+1 и при удалении висячих вершин эксцентриситеты оставшихся уменьшаются на 1. Следовательно, при удалении висячих вершин центр не меняется, С(G) = С(G’>. Поскольку дерево G конечно, то удаляя на каждом шаге все висячие вершины, в конце концов за несколько шагов придём к К₁ или К₂.

Ориентированные, упорядоченные и бинарные деревья

Ориентированные (упорядоченные) деревья являются абстракцией иерархических отношений, которые очень часто встречаются как в практической жизни, так и в математике и программировании. Дерево (ориентированное) и иерархия — это равнообъёмные понятия.

Источник