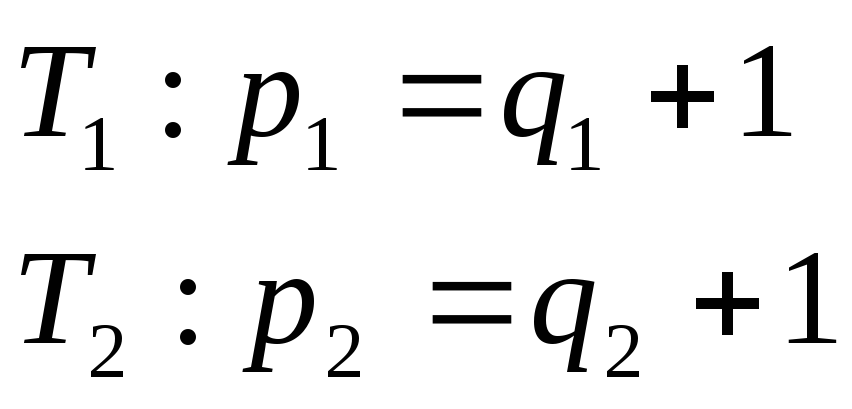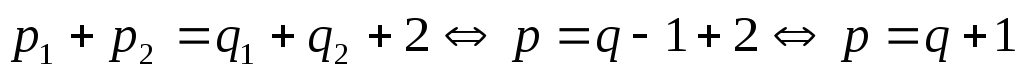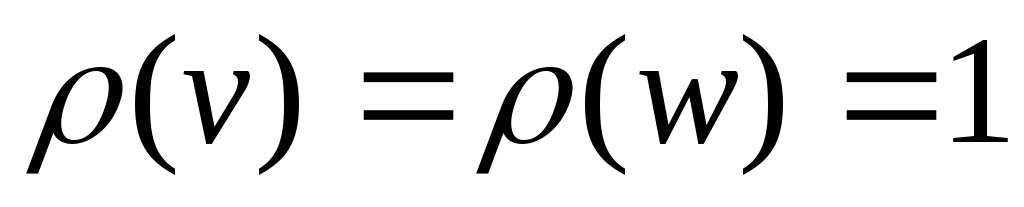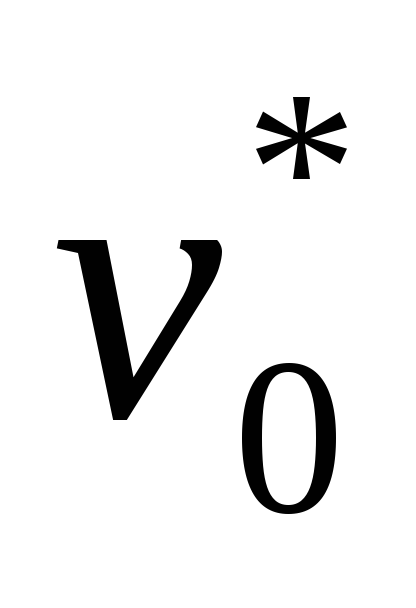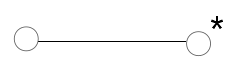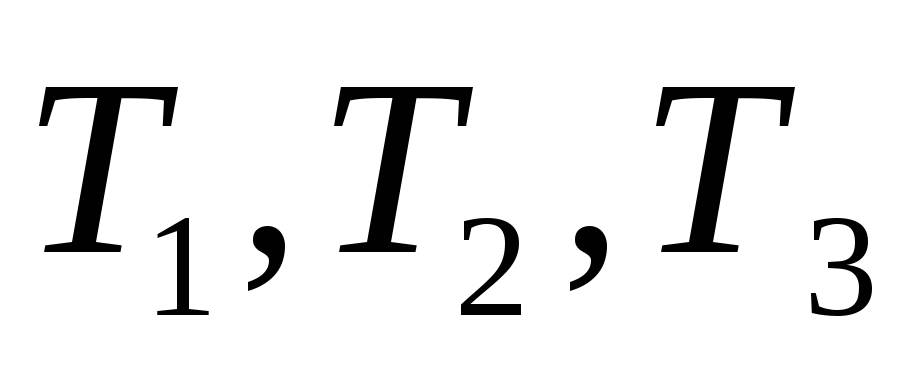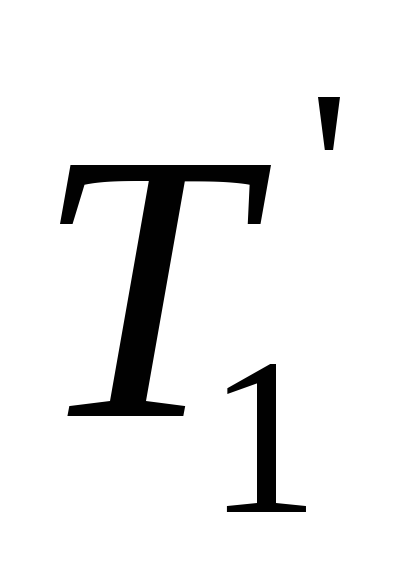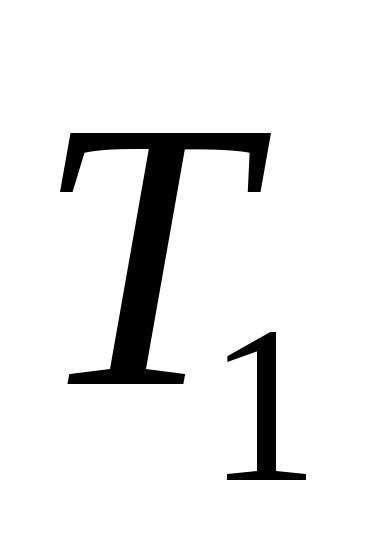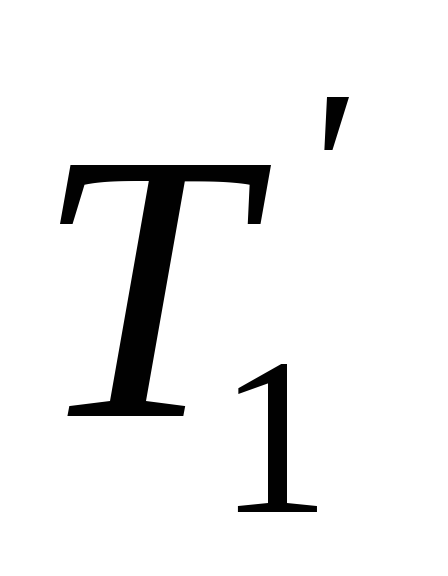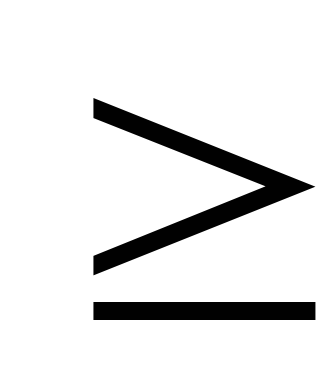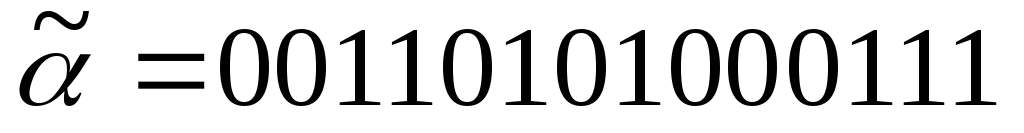Свойства степеней вершин дерева

Динамические структуры данных: бинарные деревья

Описание бинарного дерева выглядит следующим образом:

где информационное поле – это поле любого ранее объявленного или стандартного типа;

адрес левого (правого) поддерева – это указатель на объект того же типа, что и определяемая структура, в него записывается адрес следующего элемента левого (правого) поддерева .

Основными операциями, осуществляемыми с бинарными деревьями, являются:

• создание бинарного дерева ;
• печать бинарного дерева ;
• обход бинарного дерева ;
• вставка элемента в бинарное дерево ;
• удаление элемента из бинарного дерева ;
• проверка пустоты бинарного дерева ;
• удаление бинарного дерева .

Для описания алгоритмов этих основных операций используется следующее объявление:

struct BinaryTree< int Data; //поле данных BinaryTree* Left; //указатель на левый потомок BinaryTree* Right; /указатель на правый потомок >; . . . . . . . . . . BinaryTree* BTree = NULL;

Приведем функции перечисленных основных операций при работе с бинарным деревом.

//создание бинарного дерева void Make_Binary_Tree(BinaryTree** Node, int n) < BinaryTree** ptr;//вспомогательный указатель srand(time(NULL)*1000); while (n >0) < ptr = Node; while (*ptr != NULL) < if ((double) rand()/RAND_MAX < 0.5) ptr = &((*ptr)->Left); else ptr = &((*ptr)->Right); > (*ptr) = new BinaryTree(); cout > (*ptr)->Data; n--; > > //печать бинарного дерева void Print_BinaryTree(BinaryTree* Node, int l)< int i; if (Node != NULL) < Print_BinaryTree(Node->Right, l+1); for (i=0; i< l; i++) cout Data); Print_BinaryTree(Node->Left, l+1); > else cout //прямой обход бинарного дерева void PreOrder_BinaryTree(BinaryTree* Node)< if (Node != NULL) < printf ("%3ld",Node->Data); PreOrder_BinaryTree(Node->Left); PreOrder_BinaryTree(Node->Right); > > //обратный обход бинарного дерева void PostOrder_BinaryTree(BinaryTree* Node)< if (Node != NULL) < PostOrder_BinaryTree(Node->Left); PostOrder_BinaryTree(Node->Right); printf ("%3ld",Node->Data); > > //симметричный обход бинарного дерева void SymmetricOrder_BinaryTree(BinaryTree* Node)< if (Node != NULL) < PostOrder_BinaryTree(Node->Left); printf ("%3ld",Node->Data); PostOrder_BinaryTree(Node->Right); > > //вставка вершины в бинарное дерево void Insert_Node_BinaryTree(BinaryTree** Node,int Data) < BinaryTree* New_Node = new BinaryTree; New_Node->Data = Data; New_Node->Left = NULL; New_Node->Right = NULL; BinaryTree** ptr = Node;//вспомогательный указатель srand(time(NULL)*1000); while (*ptr != NULL) < double q = (double) rand()/RAND_MAX; if ( q < 1/3.0) ptr = &((*ptr)->Left); else if ( q > 2/3.0) ptr = &((*ptr)->Right); else break; > if (*ptr != NULL) < if ( (double) rand()/RAND_MAX < 0.5 ) New_Node->Left = *ptr; else New_Node->Right = *ptr; *ptr = New_Node; > else < *ptr = New_Node; >> //удаление вершины из бинарного дерева void Delete_Node_BinaryTree(BinaryTree** Node,int Data)< if ( (*Node) != NULL )< if ((*Node)->Data == Data)< BinaryTree* ptr = (*Node); if ( (*Node)->Left == NULL && (*Node)->Right == NULL ) (*Node) = NULL; else if ((*Node)->Left == NULL) (*Node) = ptr->Right; else if ((*Node)->Right == NULL) (*Node) = ptr->Left; else < (*Node) = ptr->Right; BinaryTree ** ptr1; ptr1 = Node; while (*ptr1 != NULL) ptr1 = &((*ptr1)->Left); (*ptr1) = ptr->Left; > delete(ptr); Delete_Node_BinaryTree(Node,Data); > else < Delete_Node_BinaryTree(&((*Node)->Left),Data); Delete_Node_BinaryTree(&((*Node)->Right),Data); > > > //проверка пустоты бинарного дерева bool Empty_BinaryTree(BinaryTree* Node) < return ( Node == NULL ? true : false ); >//освобождение памяти, выделенной под бинарное дерево void Delete_BinaryTree(BinaryTree* Node)< if (Node != NULL) < Delete_BinaryTree(Node->Left); Delete_BinaryTree(Node->Right); delete(Node); > >

Ключевые термины

Бинарное (двоичное) дерево – это дерево , в котором каждая вершина имеет не более двух потомков.

Вершина (узел) дерева – это каждый элемент дерева.

Ветви дерева – это направленные дуги, которыми соединены вершины дерева.

Высота (глубина) дерева – это количество уровней, на которых располагаются его вершины.

Дерево – это структура данных , представляющая собой совокупность элементов и отношений, образующих иерархическую структуру этих элементов.

Корень дерева – это начальный узел дерева, ему соответствует нулевой уровень.

Листья дерева – это вершины, в которые входит одна ветвь и не выходит ни одной ветви.

Неполное бинарное дерево – это дерево , уровни которого заполнены не полностью.

Нестрогое бинарное дерево – это дерево , у которого вершины имеют степень ноль (у листьев), один или два (у узлов).

Обход дерева – это упорядоченная последовательность вершин дерева, в которой каждая вершина встречается только один раз.

Поддерево – это часть древообразной структуры данных, которая может быть представлена в виде отдельного дерева.

Полное бинарное дерево – это дерево , которое содержит только полностью заполненные уровни.

Потомки – это все вершины, в которые входят ветви, исходящие из одной общей вершины.

Почти сбалансированное дерево – это дерево , у которого длины всевозможных путей от корня к внешним вершинам отличаются не более, чем на единицу.

Предок – это вершина , из которой исходят ветви к вершинам следующего уровня.

Сбалансированное дерево – это дерево , у которого длины всех путей от корня к внешним вершинам равны между собой.

Степень вершины – это количество дуг, которое выходит из этой вершины.

Степень дерева – это максимальная степень вершин, входящих в дерево .

Строгое бинарное дерево – это дерево , у которого вершины имеют степень ноль (у листьев) или два (у узлов).

Упорядоченное дерево – это дерево , у которого ветви, исходящие из каждой вершины, упорядочены по определенному критерию.

Уровень вершины – это количество дуг от корня дерева до вершины.

Краткие итоги

1. Деревья являются одними из наиболее широко распространенных структур данных в программировании, которые представляют собой иерархические структуры в виде набора связанных узлов.
2. Каждое дерево обладает следующими свойствами: существует узел, в который не входит ни одной дуги (корень); в каждую вершину, кроме корня, входит одна дуга.
3. С понятием дерева связаны такие понятия, как корень, ветвь, вершина, лист, предок, потомок , степень вершины и дерева, высота дерева .
4. Списочное представление деревьев основано на элементах, соответствующих вершинам дерева.
5. Дерево можно упорядочить по указанному ключу.
6. Просмотреть с целью поиска все вершины дерева можно с помощью различных способов обхода дерева .
7. Наиболее часто используемыми обходами являются прямой, симметричный, обратный.
8. В программировании при решении большого класса задач используются бинарные деревья .
9. Бинарные деревья по степени вершин делятся на строгие и нестрогие, по характеру заполнения узлов – на полные и неполные, по удалению вершин от корня – на сбалансированные и почти сбалансированные.
10. Основными операциями с бинарными деревьями являются: создание бинарного дерева ; печать бинарного дерева ; обход бинарного дерева ; вставка элемента в бинарное дерево ; удаление элемента из бинарного дерева ; проверка пустоты бинарного дерева ; удаление бинарного дерева .
11. Бинарные деревья могут применяться для поиска данных в специально построенных деревьях (базы данных), сортировки данных, вычислений арифметических выражений , кодирования.

Источник

5.14. Деревья и их свойства

– замкнутые цепи_.

_{2. Любые 2 вершины v и w соединены единственной цепью.}

_{Доказательство следует из определения дерева.}

_{3. Для дерева справедливо следующее соотношение: p = q + 1 (*), где p – число вершин, q – число ребер.}

_{Доказательство (индукцией по p):}

_{а) p = 1 – дерево состоит из одной вершины, q = 0, тогда соотношение (*) выглядит 1 = 1.}

_{б) Пусть соотношение (*) верно для любых деревьев, у которых вершин меньше, чем p.}

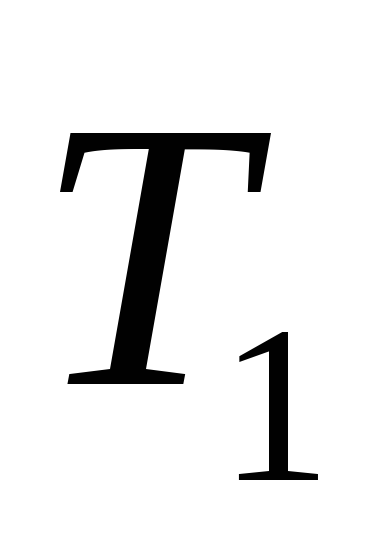
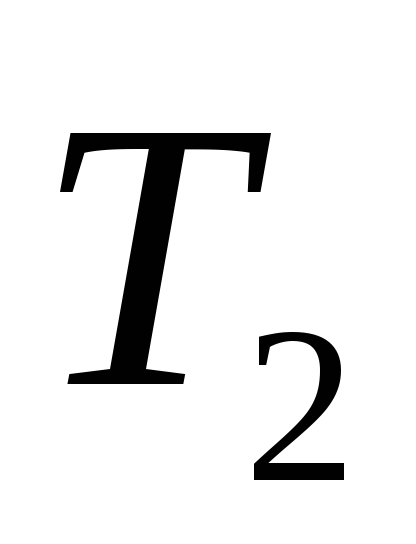
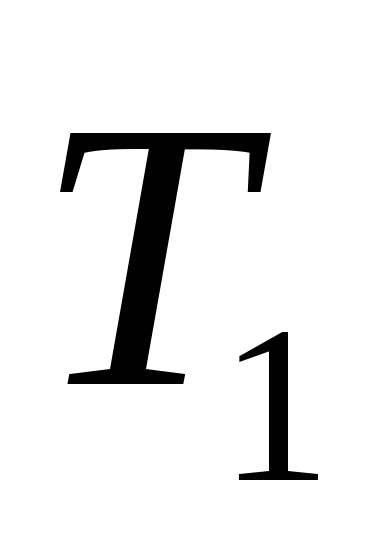
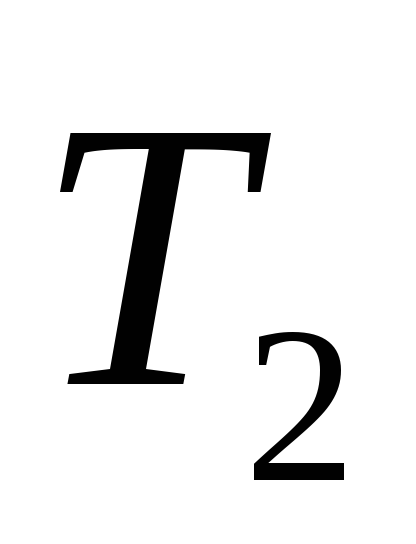
_{в) Рассмотрим дерево с p вершинами. Уберем ребро, соединяющее вершины v и w. Наш граф разбился на 2 подграфа и . , – деревья, так как они связны и не имеют замкнутых цепей. Поэтому для них верно индукционное предположение:}

_{VWV W}

_.

_{4. Если любые 2 вершины v и w в дереве соединить ребром, то получим ровно одну замкнутую цепь.}

_{Доказательство следует из свойства 2.}

_{5. Пусть G = (p, q) – дерево, где p > 1. Тогда в дереве G существуют хотя бы 2 вершины v и w такие, что .}

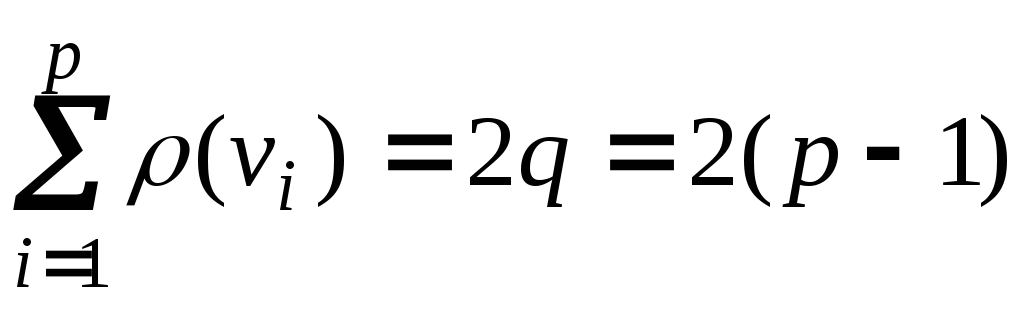
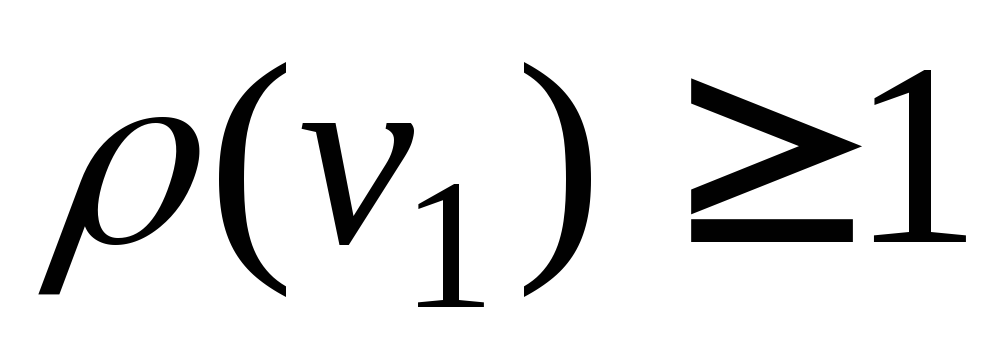
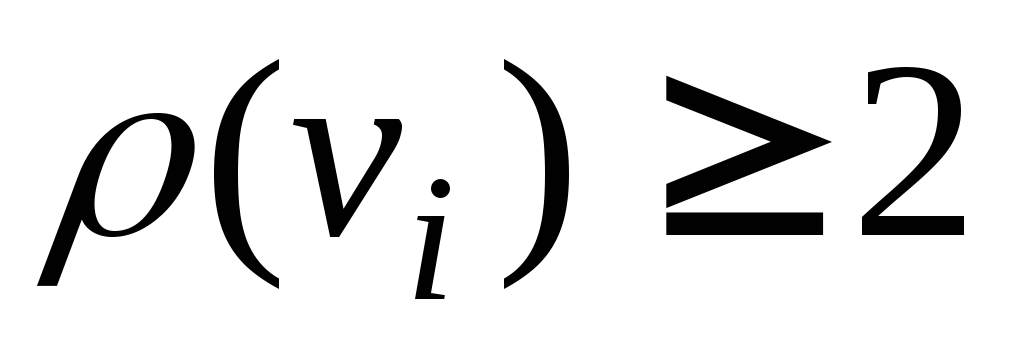
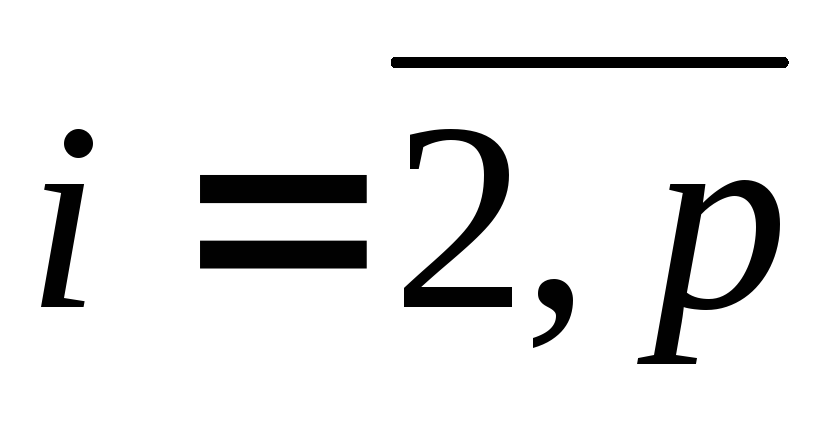
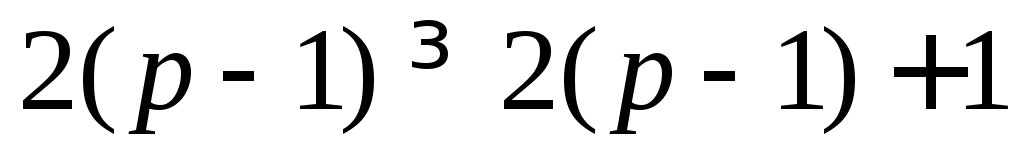
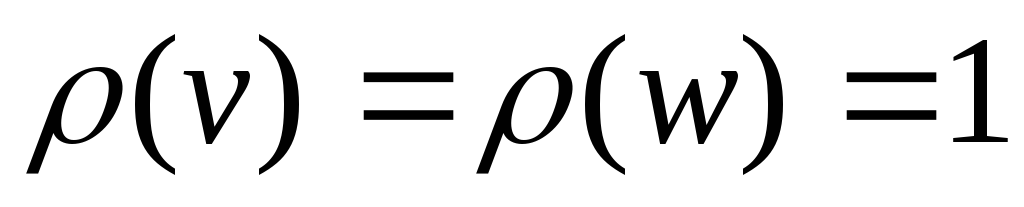
_{Доказательство. Как известно, (по свойству 3). Предположим, что не существуют 2 вершины, степень которых равна 1, т.е. пусть , а у остальных вершин , где . Тогда получаем, что . Пришли к противоречию, значит, существуют вершины v и w такие, что .}

_{Определение. Вершины в дереве, степень которых равна 1, называются концевыми.}

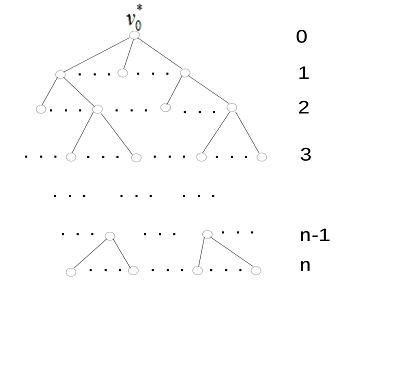
_{где max(n) – глубина (количество ярусов) дерева, – корень дерева (корень – это некоторая выделенная вершина).}

5.15. Деревья и операции над ними

_{1. Ребро – дерево с корнем (код 01), дереву из одного ребра дается код 01.}

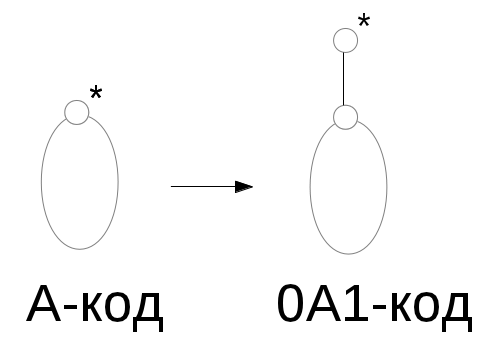
_{2. Если у нас есть дерево с корнем, то результат присоединения этого дерева к ребру – также есть дерево с корнем.}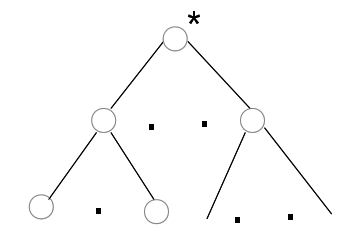

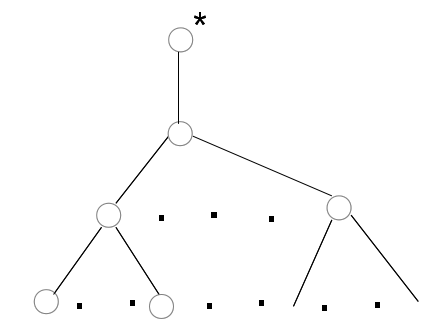
_{При этом пусть дерево с корнем имеет код А, тогда дереву, полученному в результате операции 2, ставится код 0А1.}

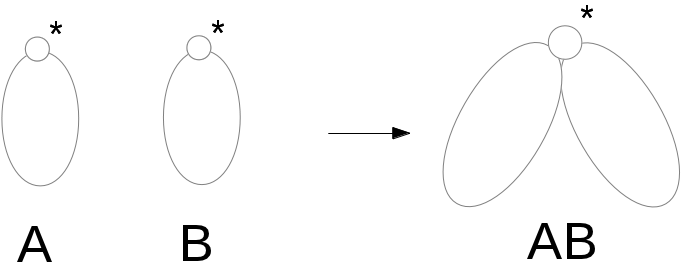
_{3. Если у нас есть два дерева с корнем,}

_{то результат склеивания этих деревьев также есть дерево с корнем. Если при этом у одного дерева код А, а у другого код В, тогда у дерева, которое получается склеиванием этих деревьев, код будет АВ.}

_{Замечание. Любое дерево с корнем можно получить при помощи вышеуказанных трех операций, при этом всегда можно определить его код.}

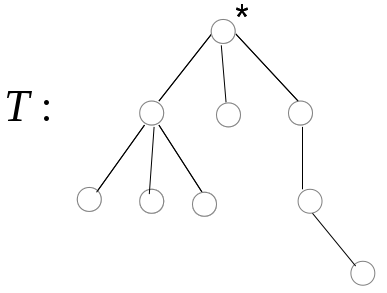
_{Пример. Пусть дано корневое дерево Т, определить его код, где}

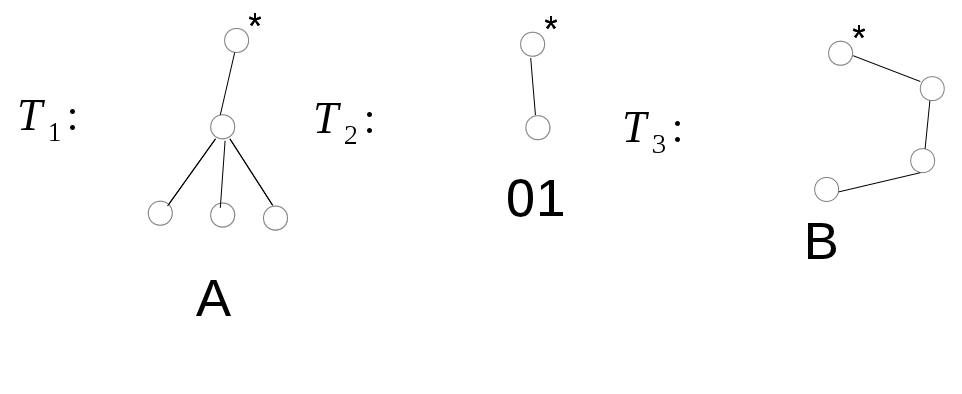
_{Решение: Исходное дерево Т получено из деревьев двукратным применением операции 3, где}

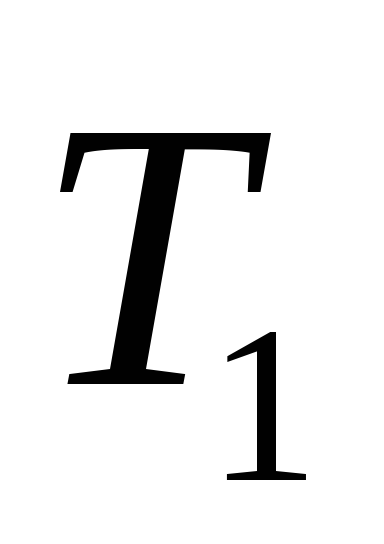
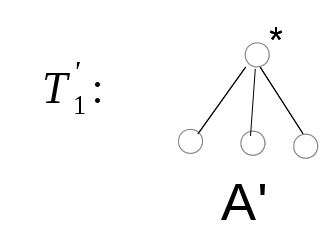
_{1) Дерево получено из дерева с помощью операции 2, где}

_,

_{Дерево получено из дерева операции 1 двукратным применением}

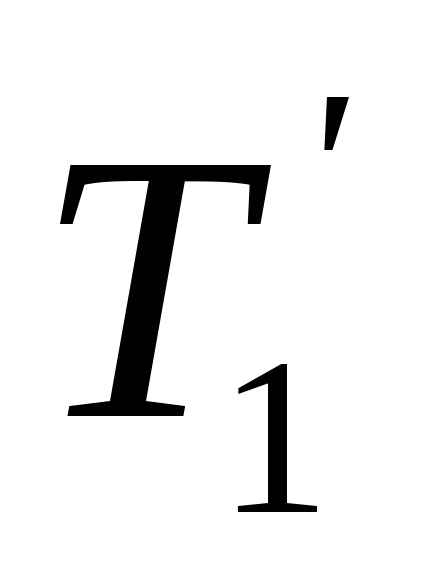
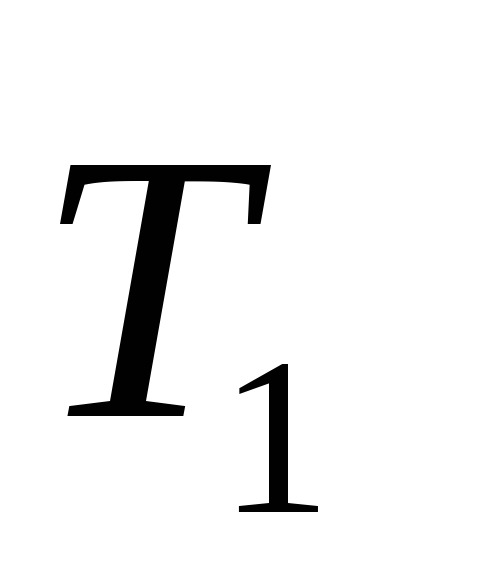
_{операции 3, тогда код дерева A‘ = 010101, следовательно, код дерева A = 00101011.}

_{2) Дерево Т2 получено с помощью операции 1, его код – 01.}

_{3) Дерево Т3 получено из дерева операции 1 двукратным применением операции 2, тогда код дерева Т3 В = 000111.}

_{В итоге код корневого дерева Т есть код А01В = 0010101101000111.}

_{1) Длина кода дерева равна удвоенному числу его ребер (2q).}

_{2) В любом начальном отрезке (если считать код дерева слева) число нулей числа единиц.}

_{3) Во всем коде число нулей равно числу единиц.}

_{Встает логичный вопрос: как восстанавливать по коду дерево?}

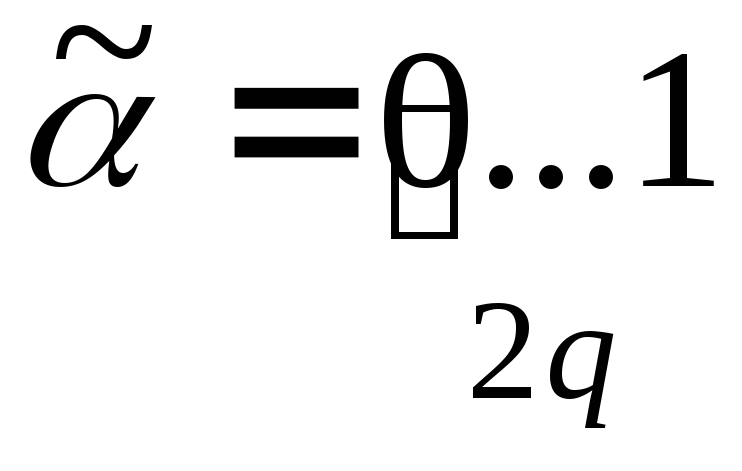
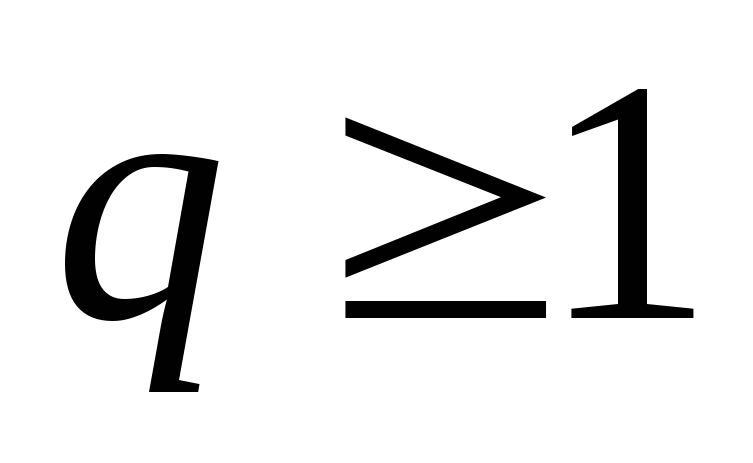
_{Берем произвольный код дерева, где , q – число ребер дерева. Идем слева направо и отмечаем такой момент, когда число нулей совпадает с числом 1. При этом возможны два случая:}

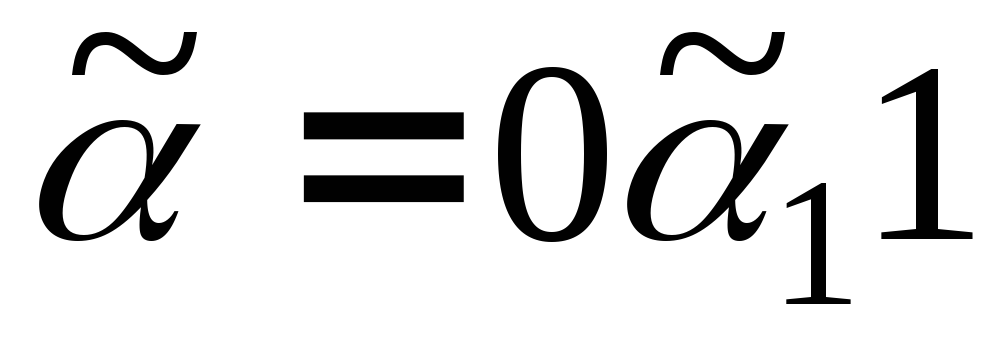
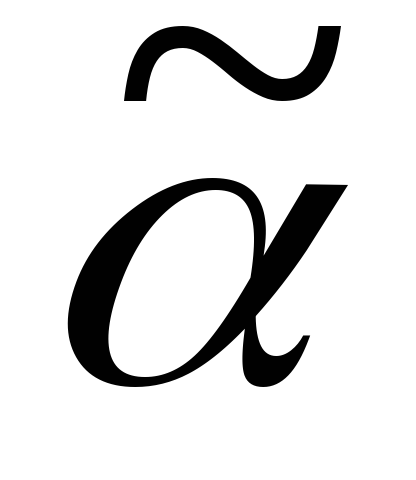
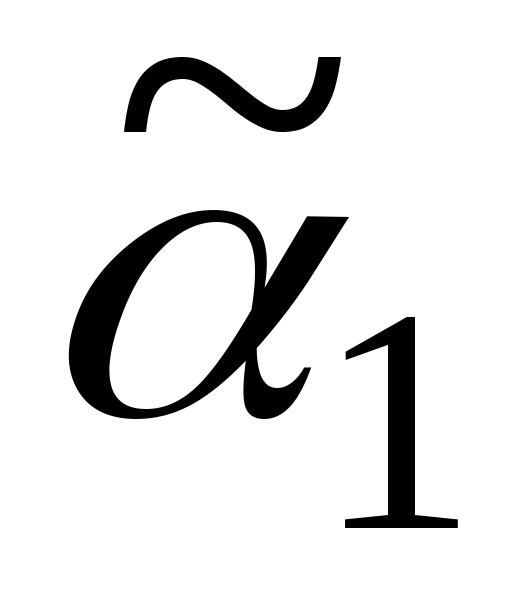
_{1) Пусть равенство наступит в конце кода, тогда , т.е. дерево с кодом получено из дерева с кодом с помощью операции 2.}

_{2) Пусть равенство наступит, не доходя до конца кода, т.е. , а это означает, что дерево с кодом получено из деревьев соответственно с кодами и с помощью операции 3.}

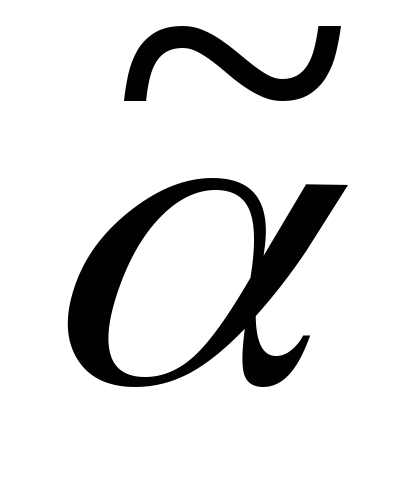
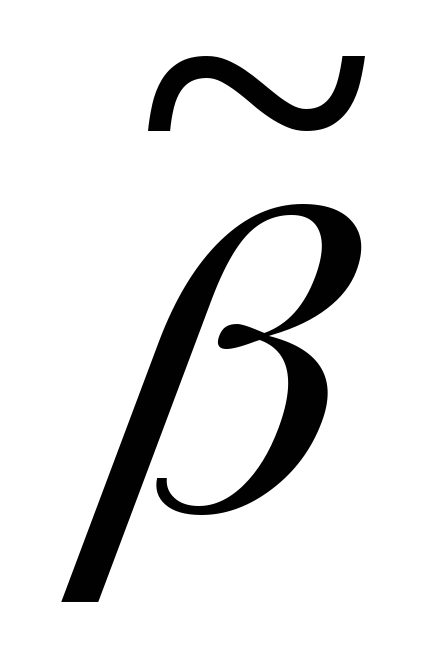
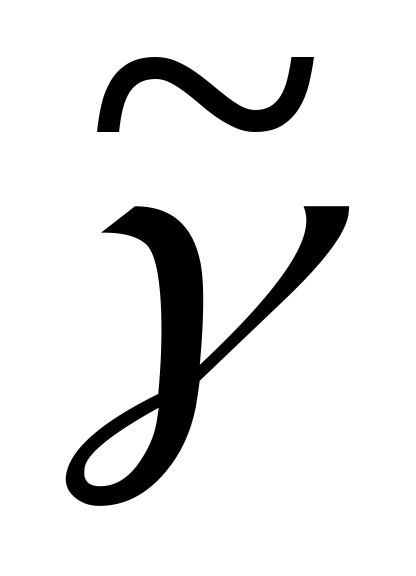
_{Аналогично, т.е. согласно пунктам 1) и 2), восстанавливаем по кодам соответствующие им деревья. Этот процесс называется декодированием. Не сложно доказать (мы практически уже показали), что между деревом и его кодом существует взаимно однозначное соответствие.}

_{Пример. Построить корневое дерево по его коду .}

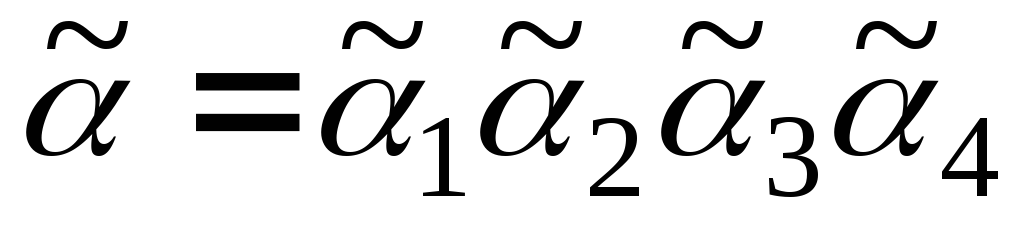
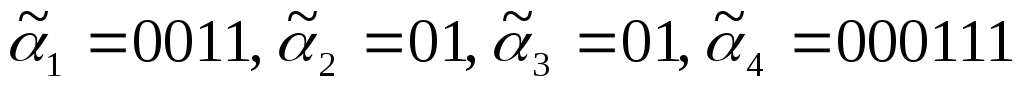
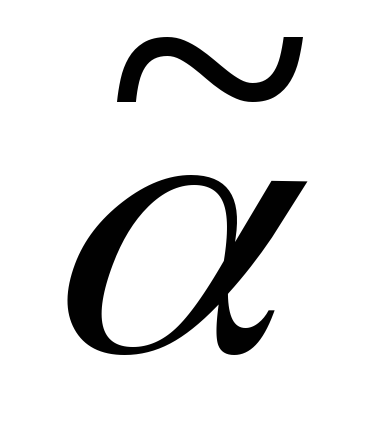
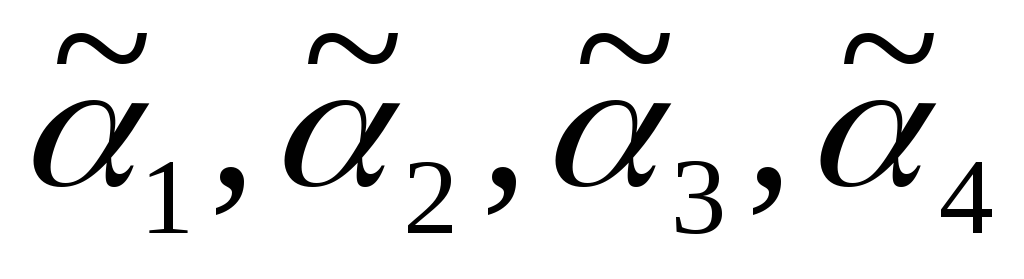
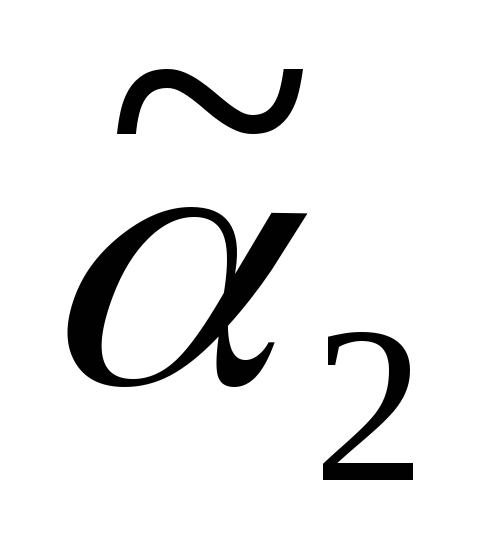
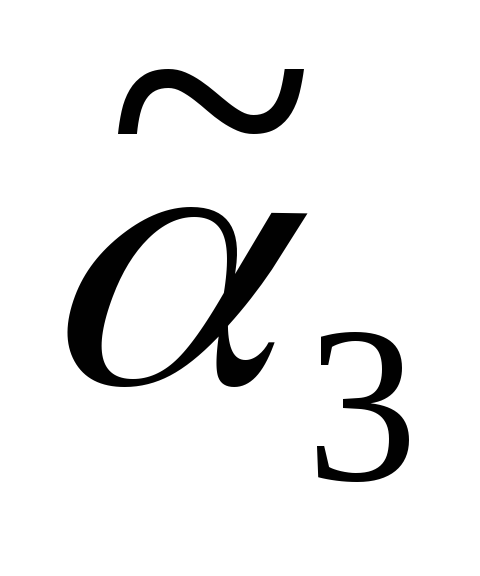
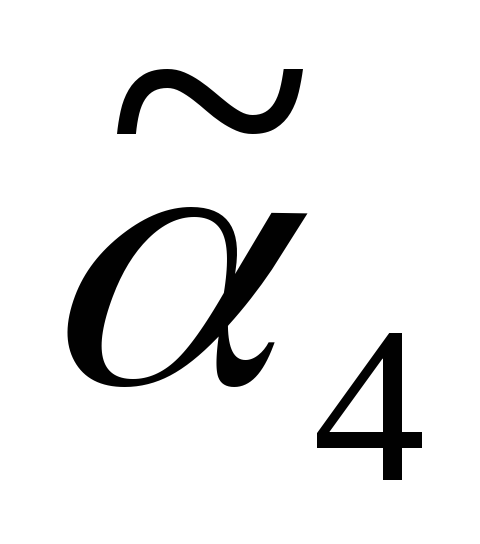
_{Решение: q = 7. , где . Таким образом, дерево с кодом получено из деревьев соответственно с кодами с трехкратным применением операции 3. Аналогично, дерево с кодом получено из дерева операции 1 с применением операции 2; деревья с кодами и – деревья операции 1; дерево с кодом получено из дерева операции 1 с двукратным применением операции 2. В итоге дерево Т выглядит следующим образом:}

Источник