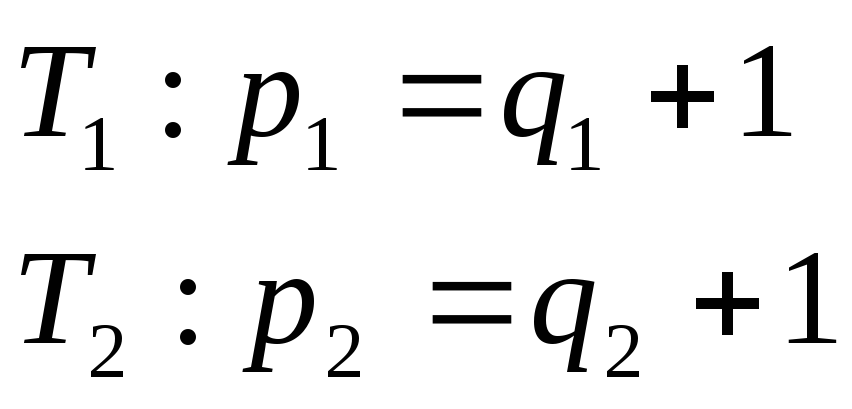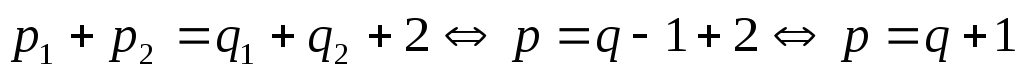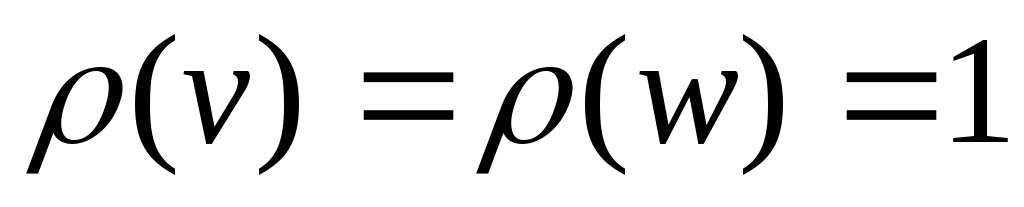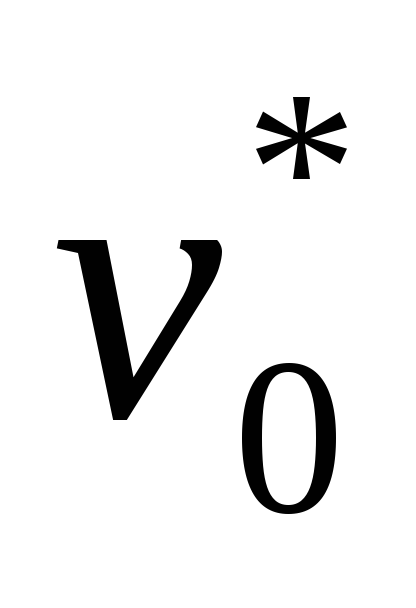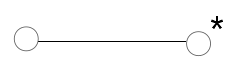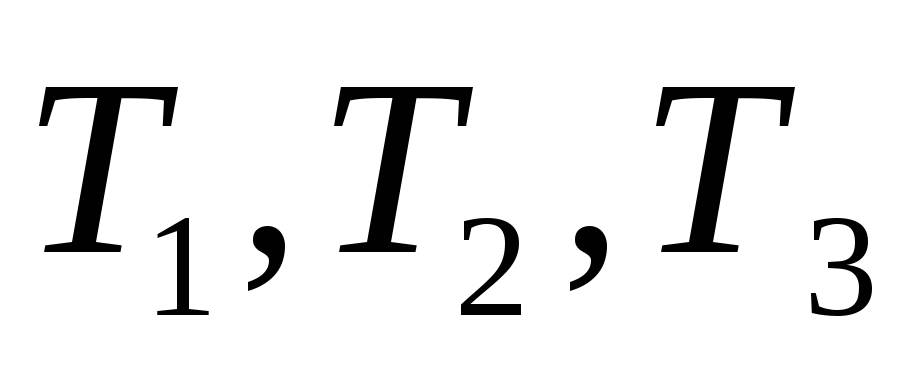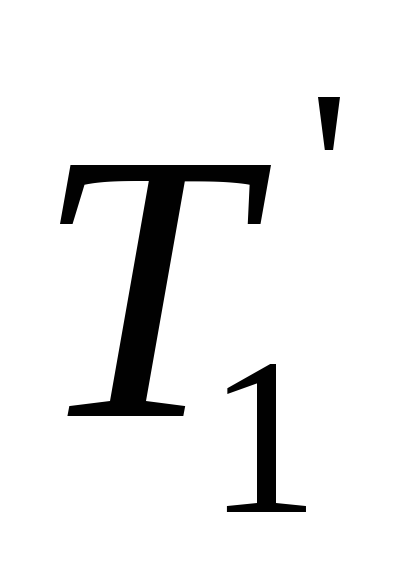Определение и свойства деревьев.
Деревом называется произвольный связный граф без циклов. Деревья обладают следующими свойствами:
любые две вершины соединены единственной простои цепью
количество ребер на единицу меньше количества вершин
при удалении любого ребра дерево становится не связным графом
при добавлении к дереву любого ребра в дереве появляется ровно один простой цикл.
Фактически дерево можно получить из любого связного графа
Утверждение: любой связный граф содержит остовный подграф который является деревом. Этот подграф называется остовыным деревом.
Специальные виды деревьев
1 Корневые деревья
Определение: Корневое дерево — ориентированное дерево, которое удовлетворяет условиям:
a) Имеется ровно один узел в который не входит не одно
В каждый узел кроме корня входит ровно одно ребро
Из корня имеется путь к любому ребру.
Если имеется путь от вершины vl к вершине v2, тогда вершина vl предок вершины v2, а вершина v2 потомок вершины vl.
Вершина которая не имеет потомков называется концевой вершиной или листом. Не концевую вершину называют внутренней. Если V1 и V2 дуга корневого дерева, то V1— отец, a V2— сын
Глубина дерева — длина пути из корня. Узлы находящиеся на одной глубине называются ярусами дерева.
Для задания корневого дерева можно использовать те же способы, что и для любого графа. На практике для представления деревьев используется канонический способ: для каждого узла хранится указатель на отца.
2 Бинарные деревья
Определение: Бинарное дерево — корневое дерево у каждой вершины которого не более двух сыновей.
В таком дереве любой произвольный узел имеет левого и правого сына. Поддерево корнем которого является левый сын называется левым поддеревом. Поддерево корнем которого является правый сын называется правым поддеревом.
Имеется два способа представления бинарных деревьев:
1. Представление в виде двух массивов: первый массив- левые сыновья, второй — правые.
2. Представление в виде списковой структуры tree_ ptr Tree_mode — запись имеющая структуру:
Element- тип узла; Left: tree_ ptr; Right: tree_ ptr;
3 Полные бинарные деревья
Определение: Полное бинарное дерево — бинарное дерево для которого выполняются условия:
a) Заполнение дерева осуществляется от корня к листьям по уровням.
b) Заполнение уровней осуществляется слева направо.
Полные бинарные деревья представляются в виде одномерного массива: первый элемент массива — корень дерева. Для любого i-того узла элемент с индексом (2i) — левый сын, элемент с индексом (2i+l)- правый сын. Отец узла j — (j/2).
4 Бинарные поисковые деревья
Определение: Бинарное поисковое дерево — дерево поиска,
Все ключи в левом поддереве меньше ключа узла V
В правом поддереве все ключи больше, чем ключ V
В дереве нет одинаковых ключей.
5 Сбалансированные деревья
Определение: Дерево называется идеально сбалансированным, если оно является бинарным поисковым деревом и число вершин его левых и правых поддеревьев отличается не более, чем на единицу.
Определение: Дерево называется сбалансированным, если оно бинарное поисковое и высоты двух поддеревьев в каждой из вершин отличаются не более, чем на единицу.
6 Способы обхода узлов в бинарных деревьях
Большинство алгоритмов при работе с деревьями посещают каждый узел в некотором порядке.
Существует три наиболее распространенных способа обхода деревьев:
1. Прямой порядок: корень посещается раньше, чем поддеревья
Порядок обхода: корень — левое поддерево — правое поддерево.
Процедура организуется рекурсивно.
2. Обратный порядок (снизу вверх): корень посещается после поддеревьев.
Порядок обхода: левое поддерево — правое поддерево- корень.
3. Внутренний порядок (слева направо )
Порядок обхода: левое поддерево – корень — правое поддерево.
7 Представление множеств с помощью деревьев
Базовыми операциями над множествами являются:
определение принадлежности элемента множества.
объединение не пересекающихся множеств.
Каждое множество будем представлять в виде корневого дерева. Корень дерева можно использовать для хранения имени множества. Дерево будем представлять в каноническом виде.
Чтобы определить, к какому множеству принадлежит некоторый элемент — находим этот элемент и определяем корень множества, к которому он принадлежит. Этот корень — есть имя искомого множества.
Объединение непересекающихся множеств можем реализовать тремя способами:
Источник
Теория графов
Следующая теорема устанавливает, что два из четырех свойств – связность, ацикличность, древовидность и субцикличность – характеризуют граф как дерево.
- Для
– графа
следующие утверждения эквивалентны:
– дерево;
- Любые две несовпадающие вершины графа
соединяет единственная простая цепь;
– связный граф, и любое ребро есть мост;
– связный граф и древовидный;
– ациклический граф (лес) и древовидный;
– ациклический граф (лес) и субцикличекий;
– связный, субциклический и неполный,
;
– древовидный и субциклический, исключая
и
;
- (1->2): Если
-
Ориентированные деревья
- Ориентированным деревом (или ордеревом, или корневым деревом) называется орграф со следующими свойствами:
- существует единственный узел, в который не входит ни один другой узел. Он называется корнем ордерева;
- во все остальные узлы входит только по одному узлу;
- каждый узел достижим из корня.
- Ордерево обладает следующими свойствами:
- Концевая вершина ордерева называется листом. Путь из корня в лист называется ветвью. Длина наибольшей ветви ордерева называется высотой. Уровень узла ордерева – это расстояние отт корня до узла. Сам корень имеет уровень 0. Узлы одного уровня образуют ярус дерева.
 – дерево, то любые две его несовпадающие вершины соединяет единственная простая цепь. От противного. Пусть существуют две цепи
– дерево, то любые две его несовпадающие вершины соединяет единственная простая цепь. От противного. Пусть существуют две цепи 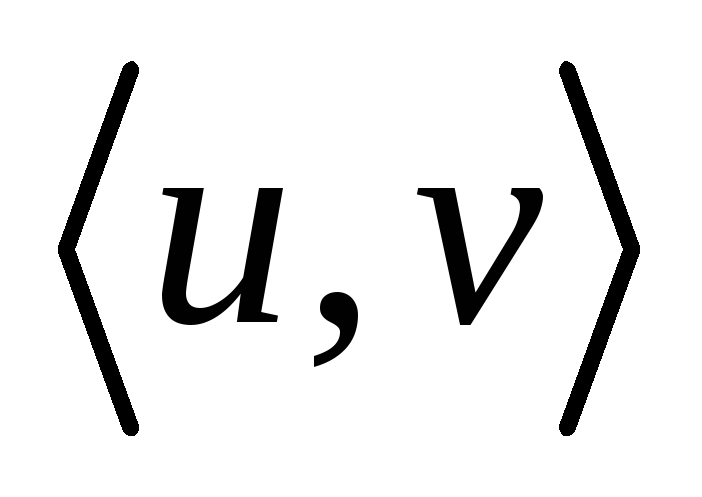 (см. рис.).
(см. рис.).  Тогда
Тогда 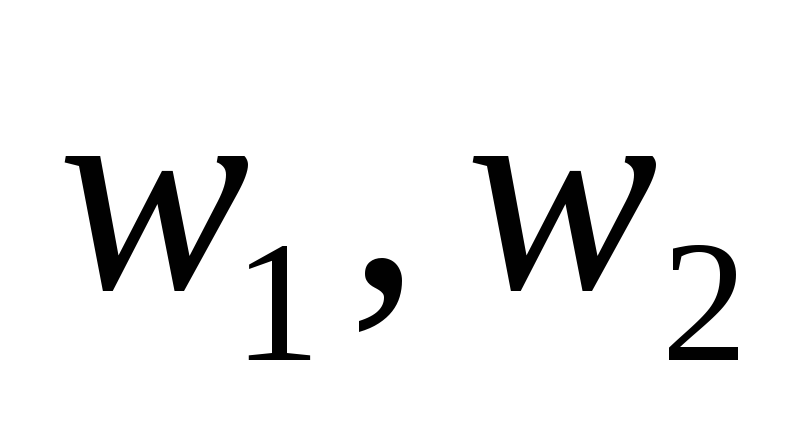 — простой цикл. (2->3): Если любые две несовпадающие вершины графа
— простой цикл. (2->3): Если любые две несовпадающие вершины графа  соединяет единственная простая цепь, то
соединяет единственная простая цепь, то  – связный граф, и любое ребро есть мост. Имеем:
– связный граф, и любое ребро есть мост. Имеем: 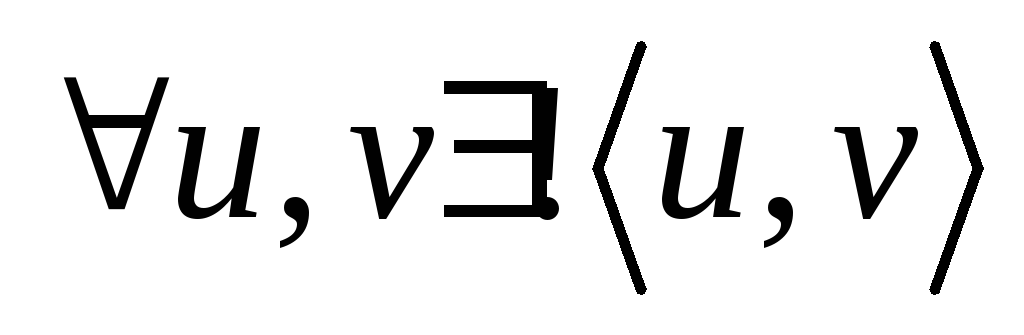

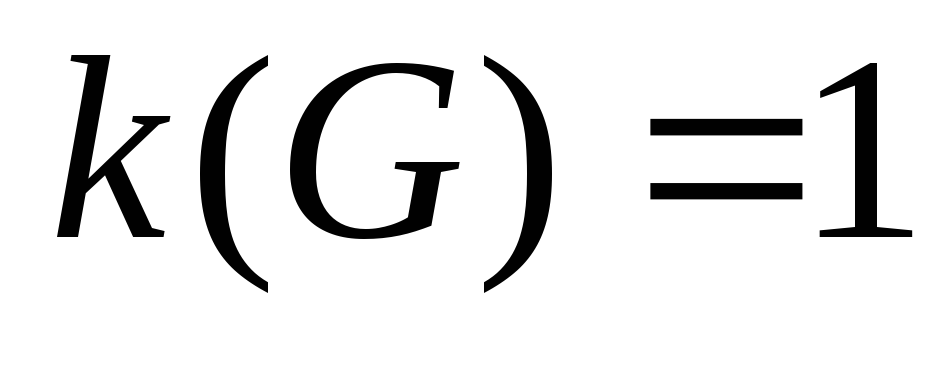 (число компонент связности). Далее от противного. Пусть ребро
(число компонент связности). Далее от противного. Пусть ребро 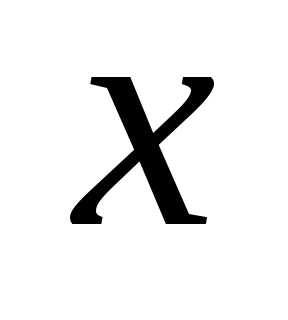 — не мост. Тогда в
— не мост. Тогда в 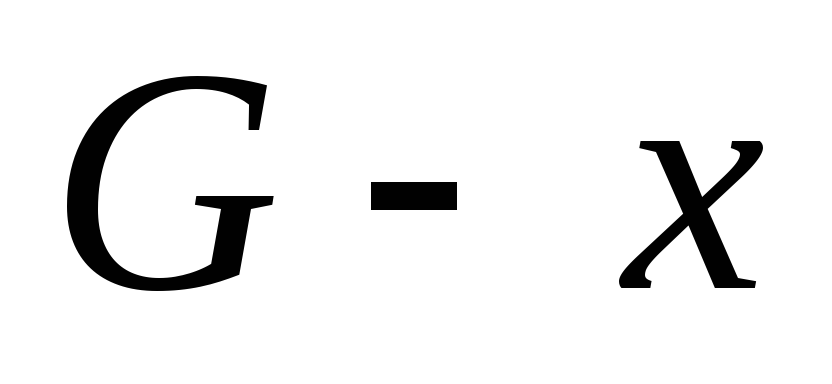 концы этого ребра связаны цепью. Само ребро
концы этого ребра связаны цепью. Само ребро 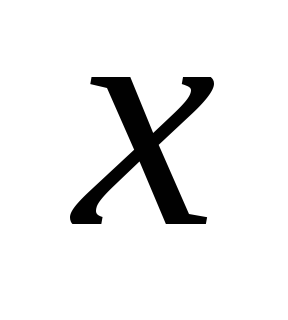 в исходном графе – вторая цепь, что противоречит условию. (3->4): Если
в исходном графе – вторая цепь, что противоречит условию. (3->4): Если  – связный граф, и любое ребро есть мост, то
– связный граф, и любое ребро есть мост, то  – связный и древовидный (
– связный и древовидный (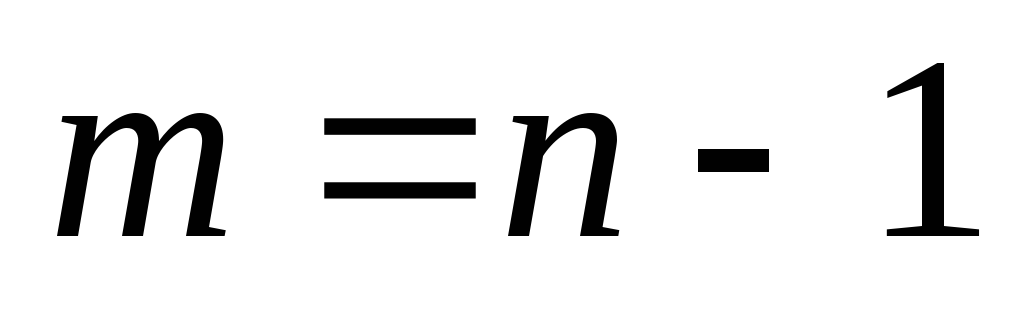 ). Индукция по
). Индукция по 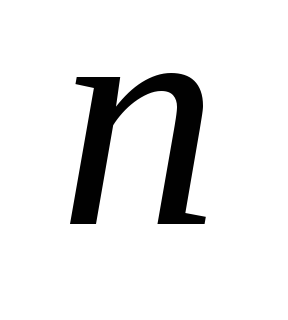 (числу вершин). Если
(числу вершин). Если 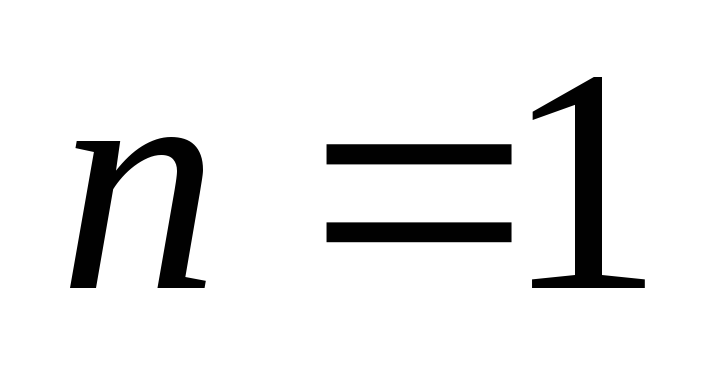 , то
, то 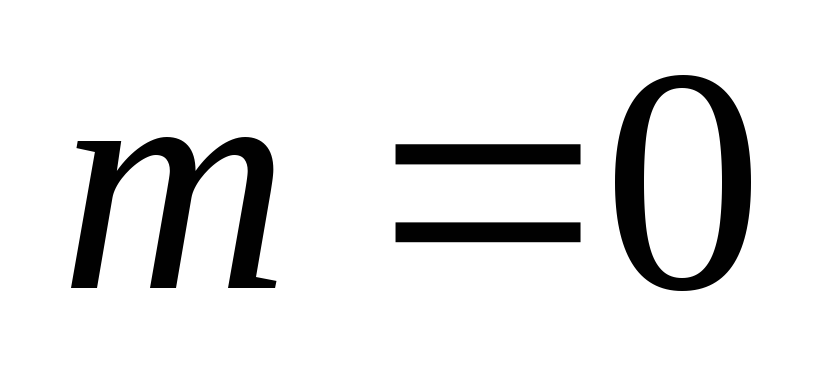 (число ребер). Пусть равенство
(число ребер). Пусть равенство 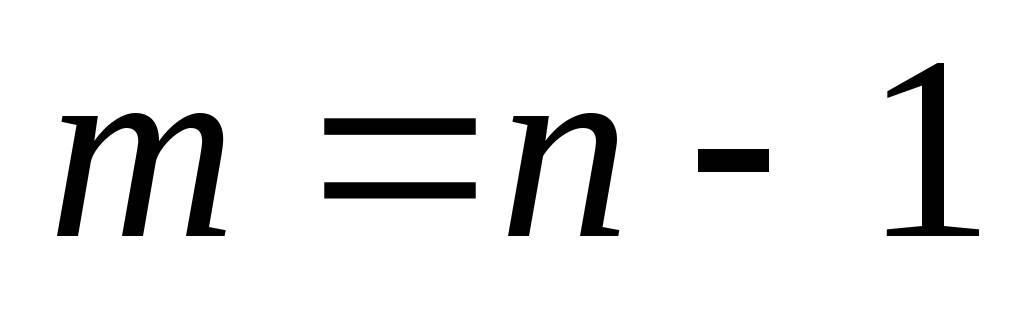 выполняется для всех графов
выполняется для всех графов  с числом вершин меньше
с числом вершин меньше 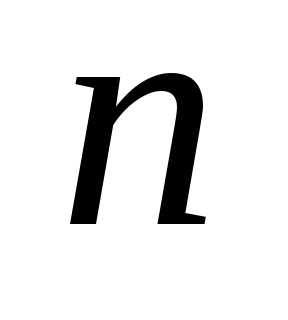 . Докажем, что оно выполняется и для
. Докажем, что оно выполняется и для 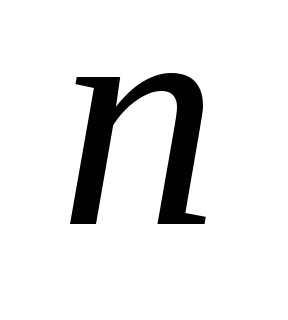 вершин. Удалим из
вершин. Удалим из  ребро
ребро 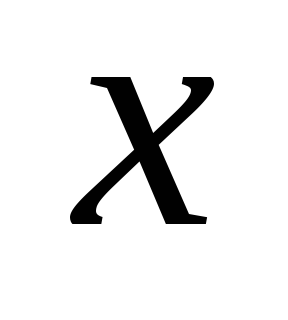 , являющееся мостом. Получим две компоненты связности
, являющееся мостом. Получим две компоненты связности  и
и  , для которых верно равенство
, для которых верно равенство 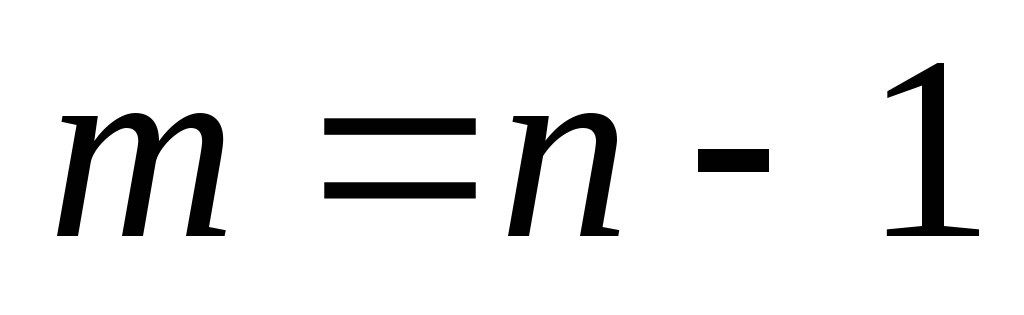 . Т.е.
. Т.е. 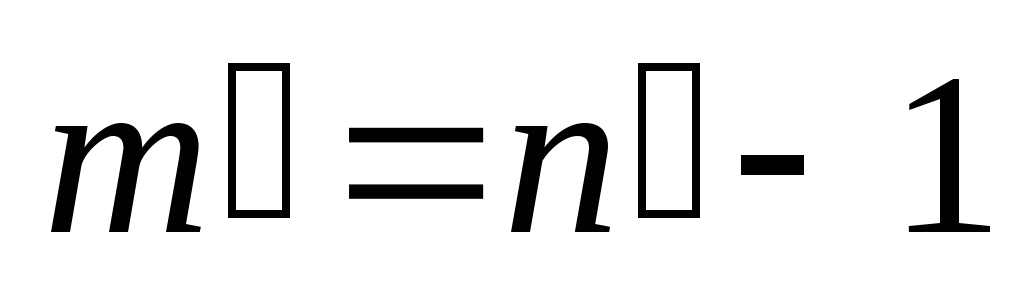 ,
, 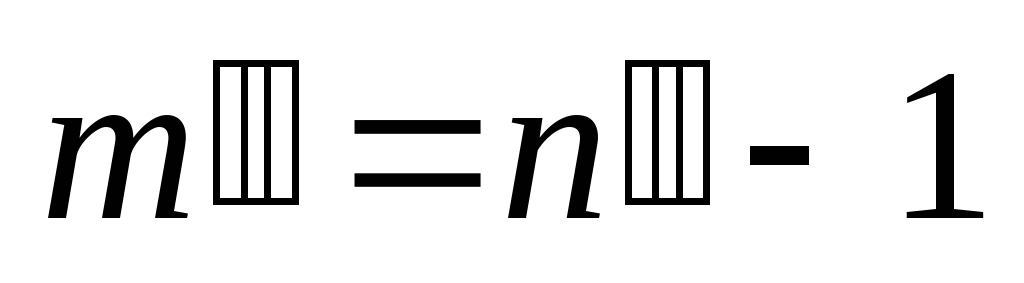 . Тогда
. Тогда  . (4->5): Если
. (4->5): Если  – связный и древовидный (
– связный и древовидный (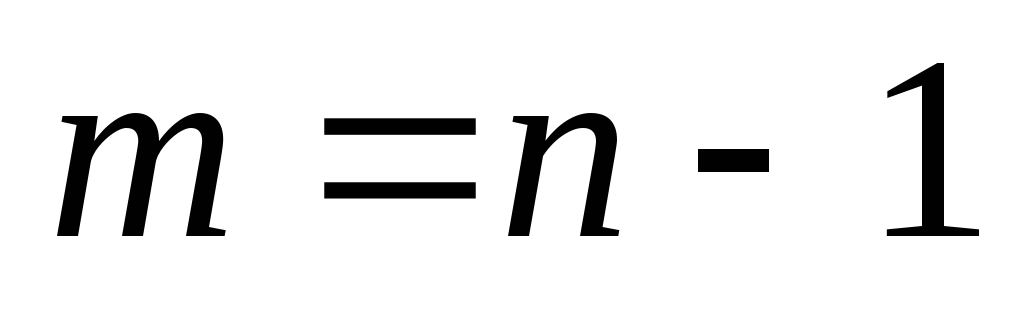 ), то
), то  – ациклический граф (лес) и древовидный (
– ациклический граф (лес) и древовидный (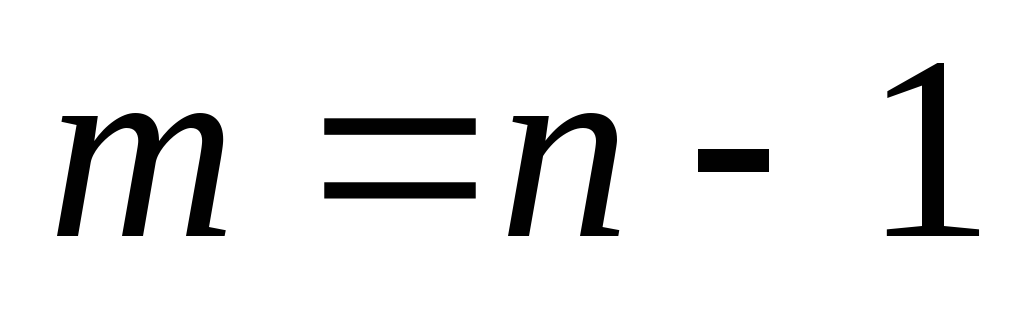 ). От противного. Пусть есть цикл с
). От противного. Пусть есть цикл с 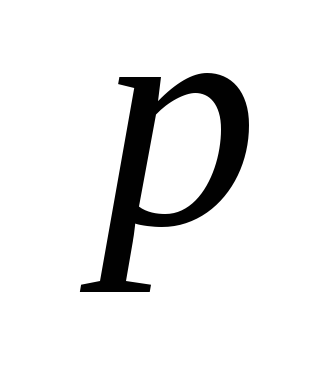 вершинами и
вершинами и  ребрами. Остальные
ребрами. Остальные 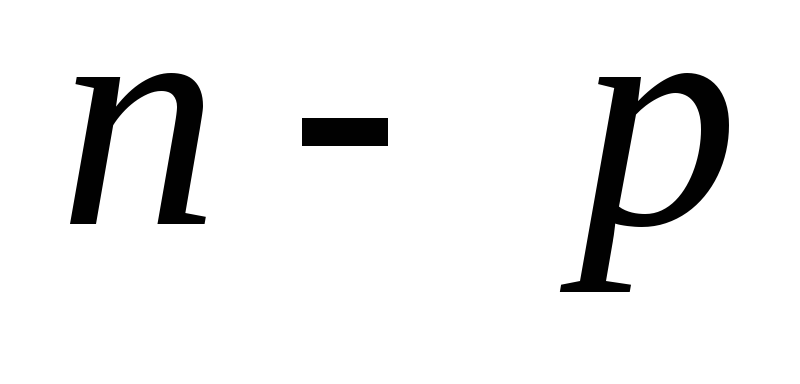 вершин связаны с этим циклом ребрами, т.к. граф связный. Следовательно,
вершин связаны с этим циклом ребрами, т.к. граф связный. Следовательно, 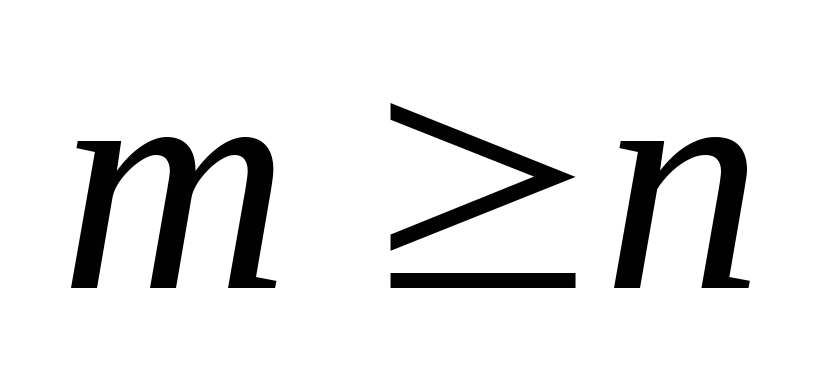 , что противоречит условию
, что противоречит условию 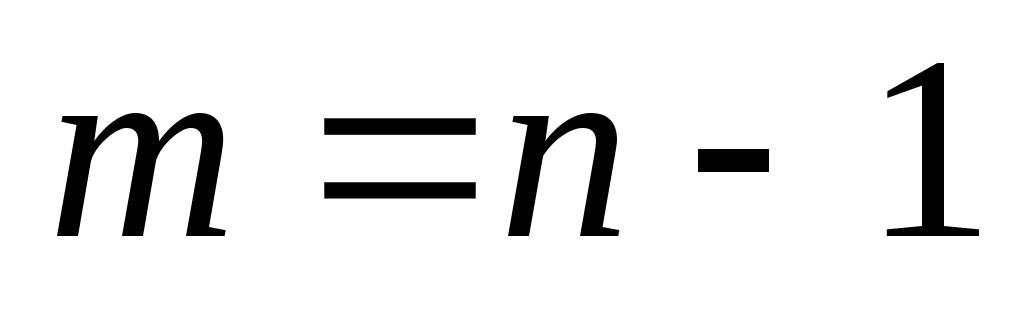 . Остальное без док-ва.
. Остальное без док-ва. 1. 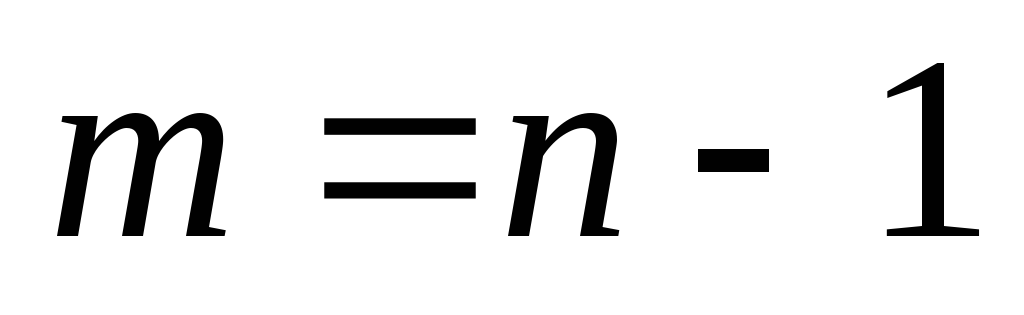
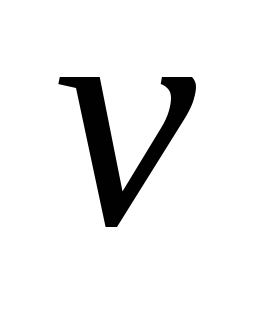
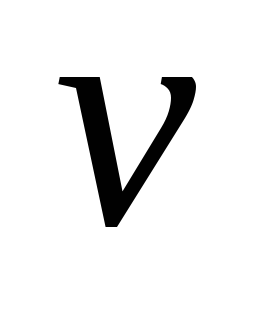
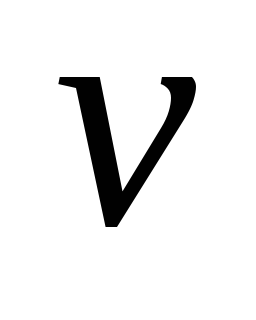
Источник
5.14. Деревья и их свойства
–

2. Любые 2 вершины v и w соединены единственной цепью.
Доказательство следует из определения дерева.
3. Для дерева справедливо следующее соотношение: p = q + 1 (*), где p – число вершин, q – число ребер.
Доказательство (индукцией по p):
а) p = 1 – дерево состоит из одной вершины, q = 0, тогда соотношение (*) выглядит 1 = 1.
б) Пусть соотношение (*) верно для любых деревьев, у которых вершин меньше, чем p.
в) Рассмотрим дерево с p вершинами. Уберем ребро, соединяющее вершины v и w. Наш граф разбился на 2 подграфа 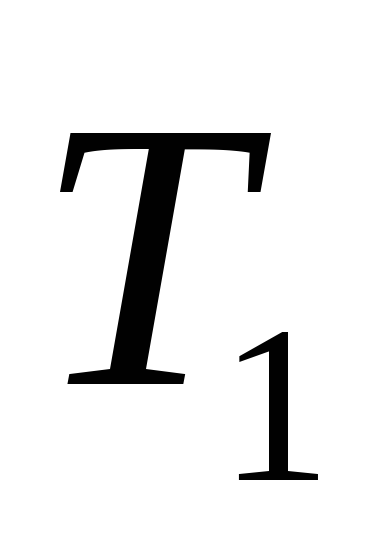
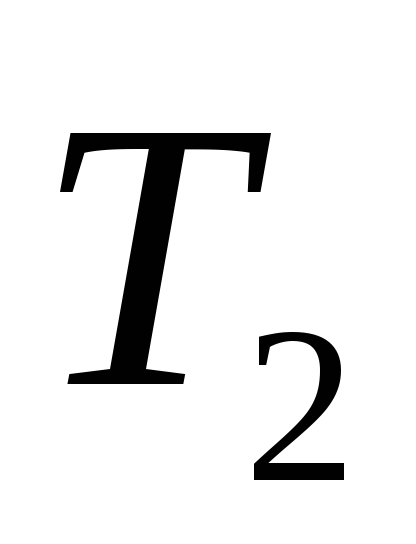
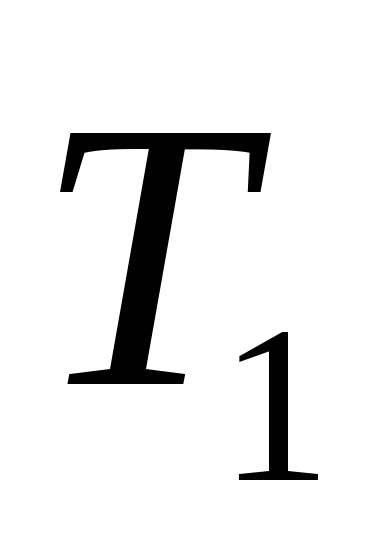
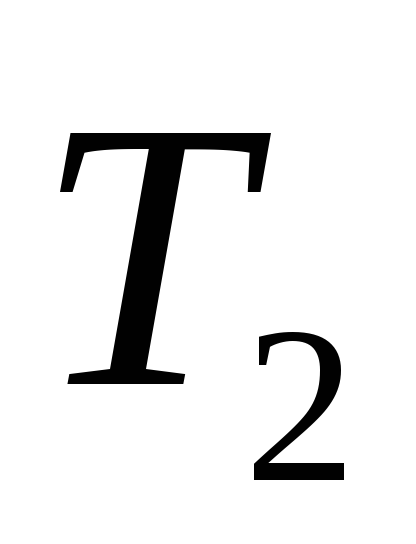
V

.
4. Если любые 2 вершины v и w в дереве соединить ребром, то получим ровно одну замкнутую цепь.
Доказательство следует из свойства 2.
5. Пусть G = (p, q) – дерево, где p > 1. Тогда в дереве G существуют хотя бы 2 вершины v и w такие, что .
Доказательство. Как известно, 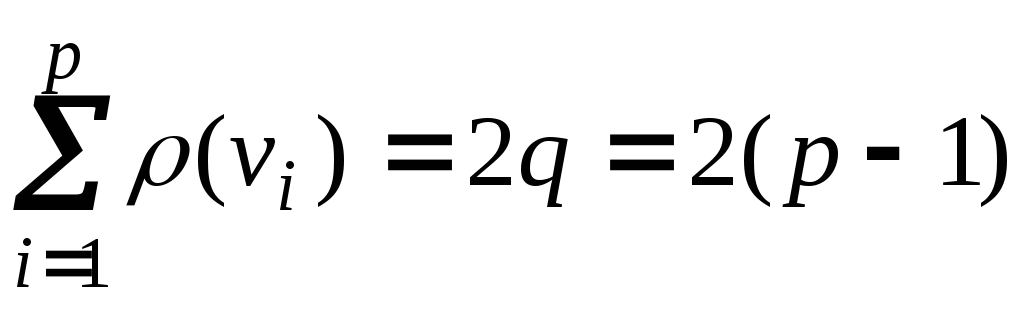
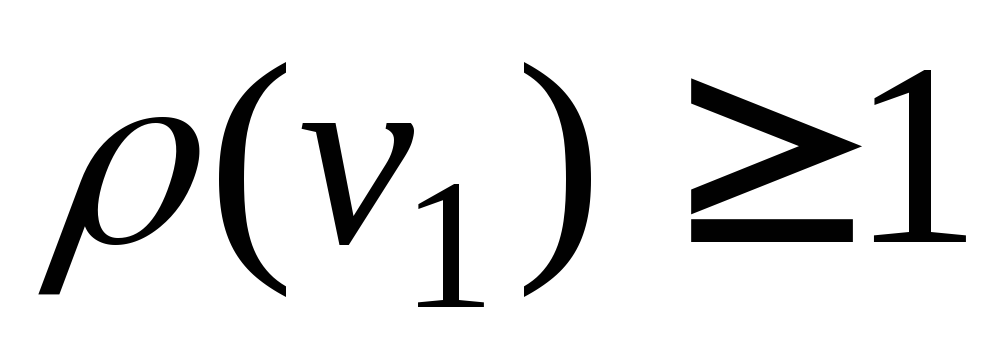
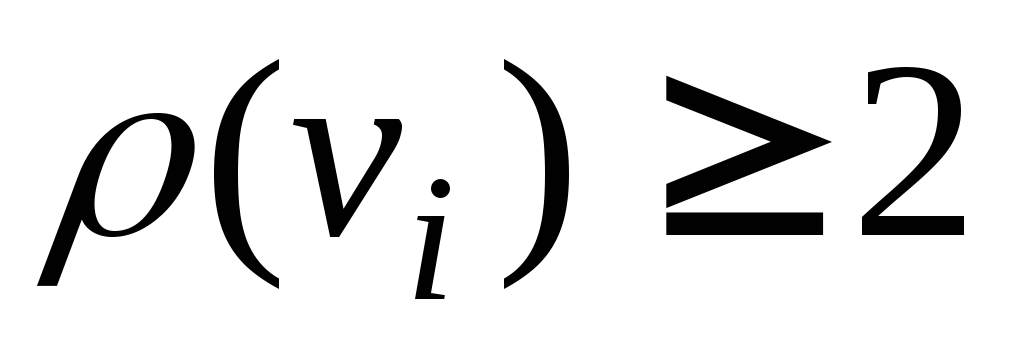
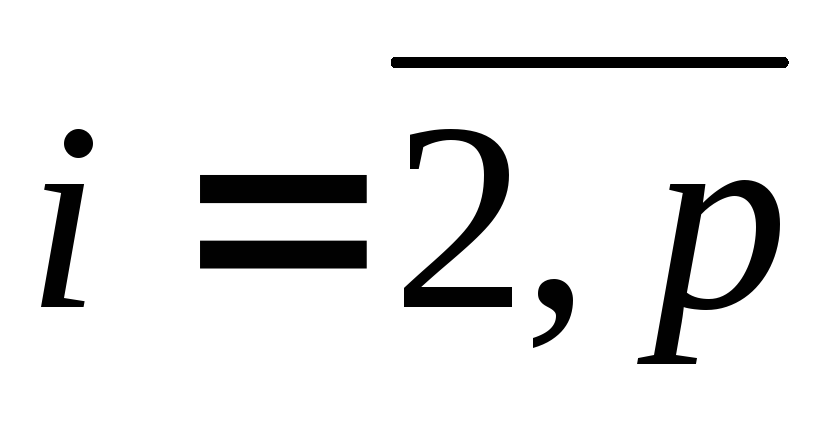
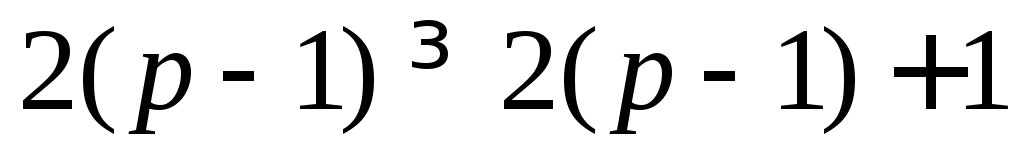
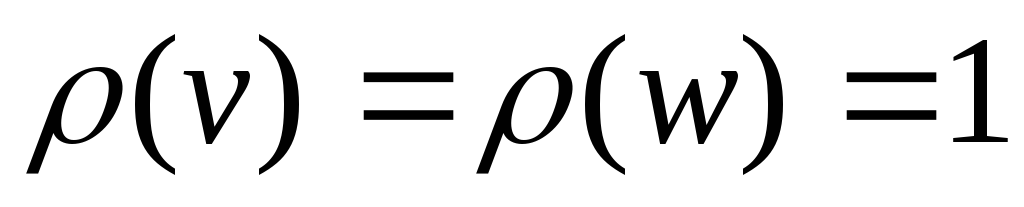
Определение. Вершины в дереве, степень которых равна 1, называются концевыми.
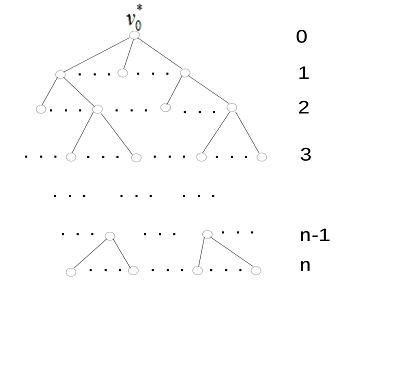
где max(n) – глубина (количество ярусов) дерева, – корень дерева (корень – это некоторая выделенная вершина).
5.15. Деревья и операции над ними
1. Ребро – дерево с корнем (код 01), дереву из одного ребра дается код 01.
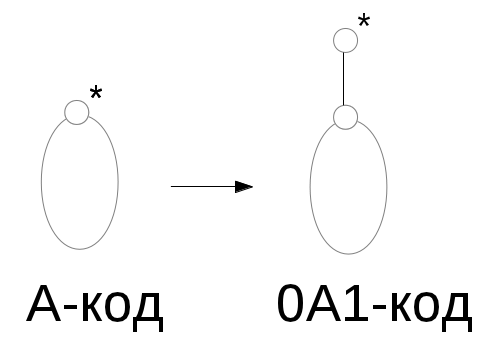
2. Если у нас есть дерево с корнем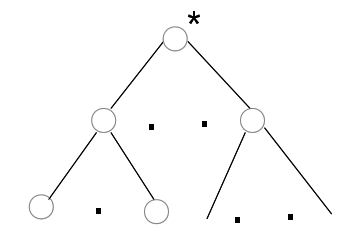
При этом пусть дерево с корнем имеет код А, тогда дереву, полученному в результате операции 2, ставится код 0А1.
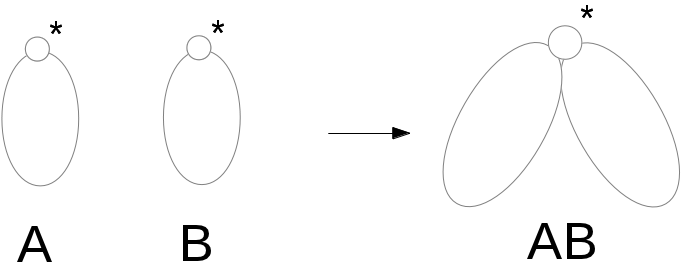
3. Если у нас есть два дерева с корнем,
то результат склеивания этих деревьев также есть дерево с корнем. Если при этом у одного дерева код А, а у другого код В, тогда у дерева, которое получается склеиванием этих деревьев, код будет АВ.
Замечание. Любое дерево с корнем можно получить при помощи вышеуказанных трех операций, при этом всегда можно определить его код.
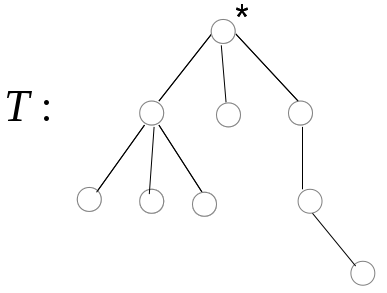
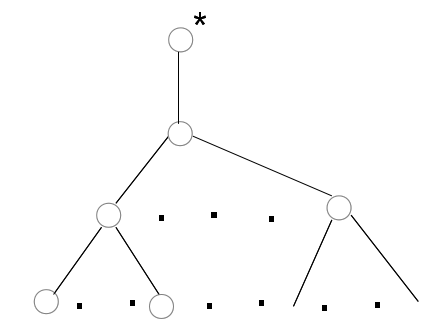
Пример. Пусть дано корневое дерево Т, определить его код, где
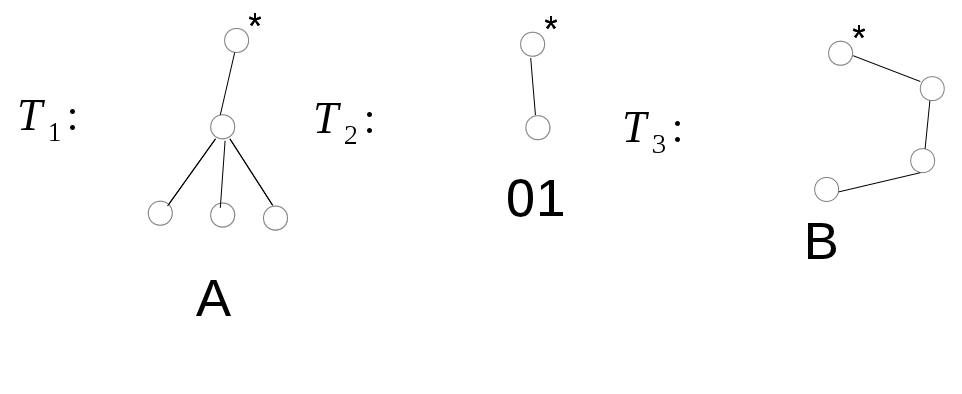
Решение: Исходное дерево Т получено из деревьев двукратным применением операции 3, где
1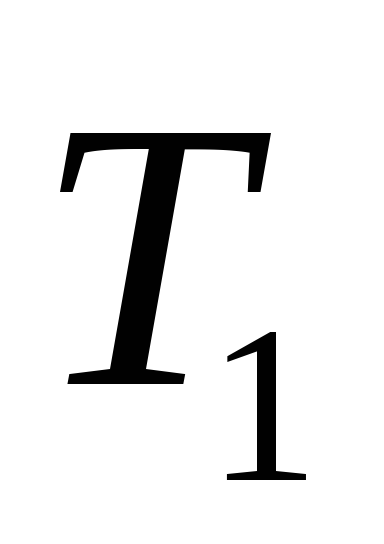
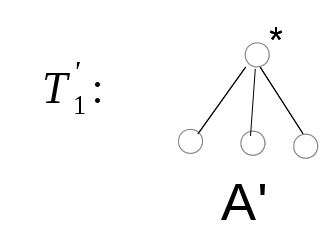
Дерево получено из дерева операции 1 двукратным применением
операции 3, тогда код дерева 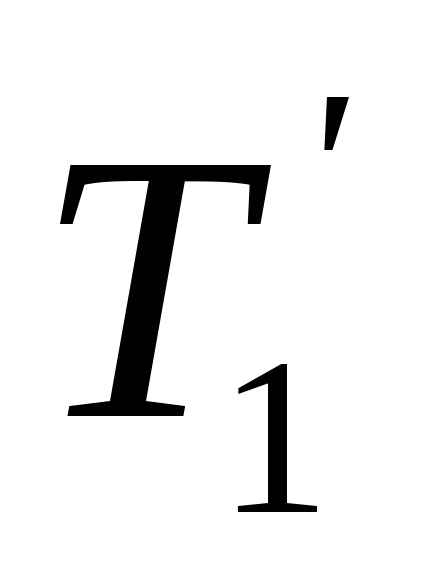
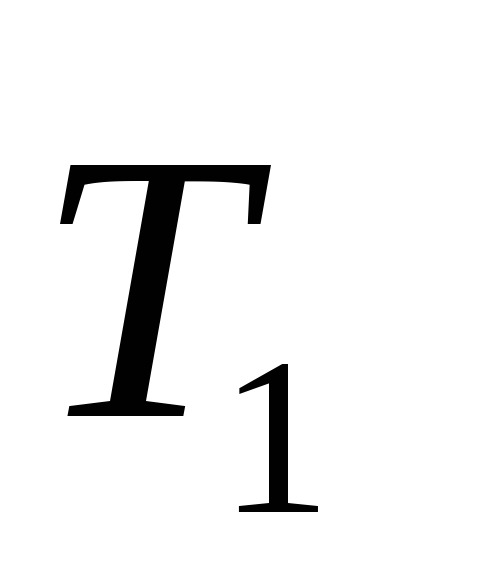
2) Дерево Т2 получено с помощью операции 1, его код – 01.
3) Дерево Т3 получено из дерева операции 1 двукратным применением операции 2, тогда код дерева Т3 В = 000111.
В итоге код корневого дерева Т есть код А01В = 0010101101000111.
1) Длина кода дерева равна удвоенному числу его ребер (2q).
2) В любом начальном отрезке (если считать код дерева слева) число нулей числа единиц.
3) Во всем коде число нулей равно числу единиц.
Встает логичный вопрос: как восстанавливать по коду дерево?
Берем произвольный код 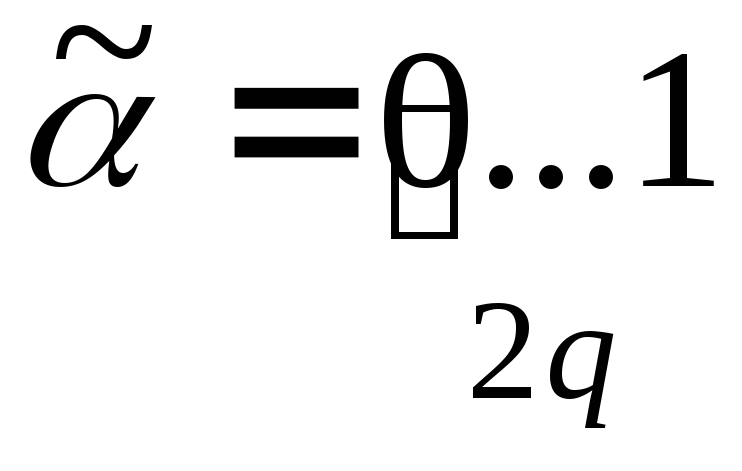
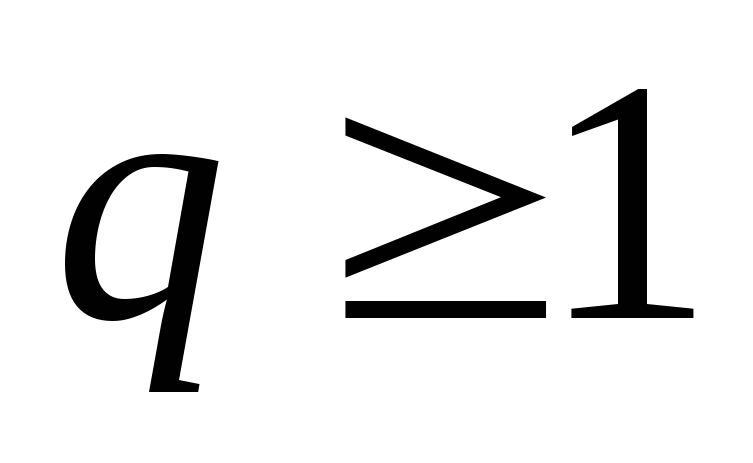
1) Пусть равенство наступит в конце кода, тогда 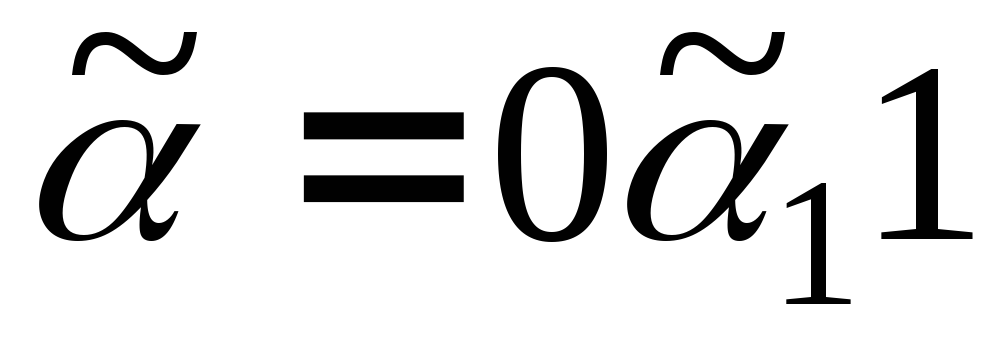
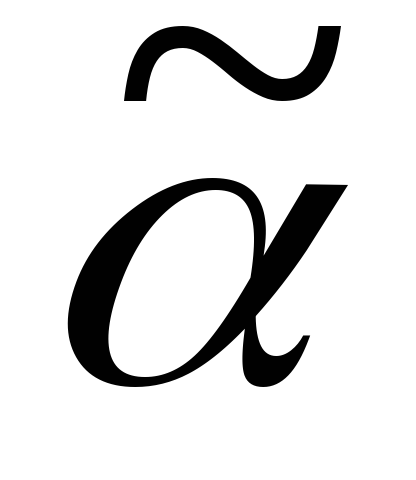
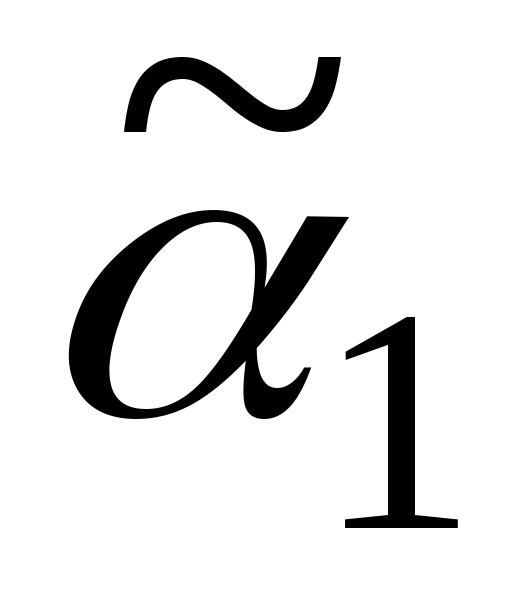
2) Пусть равенство наступит, не доходя до конца кода, т.е. 
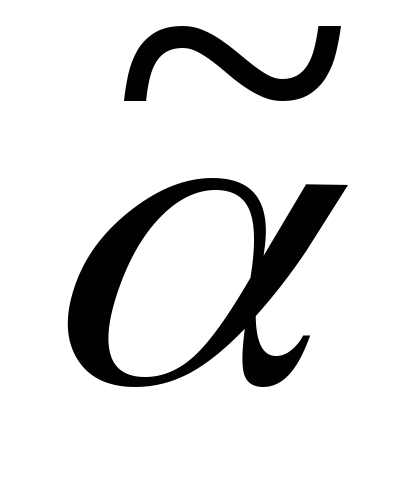
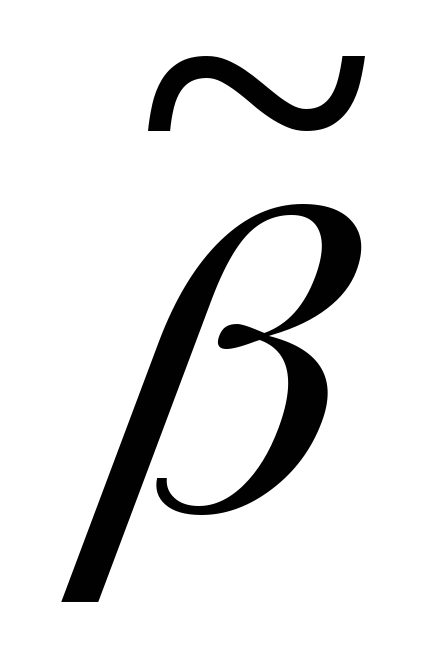
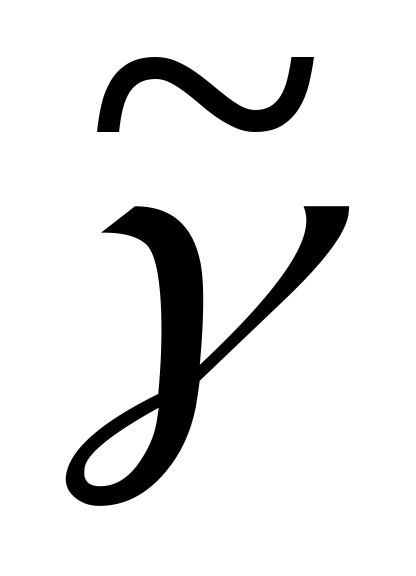
Аналогично, т.е. согласно пунктам 1) и 2), восстанавливаем по кодам соответствующие им деревья. Этот процесс называется декодированием. Не сложно доказать (мы практически уже показали), что между деревом и его кодом существует взаимно однозначное соответствие.
Пример. Построить корневое дерево по его коду .
Решение: q = 7. 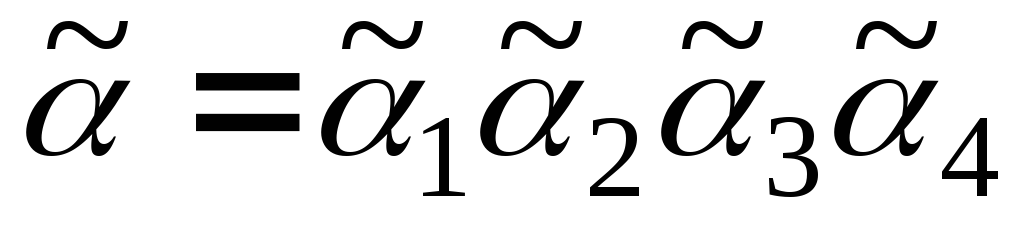
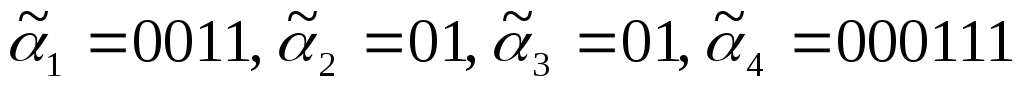
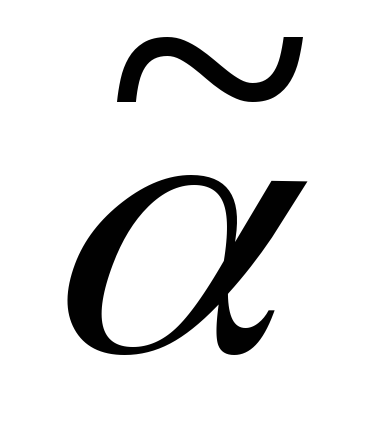
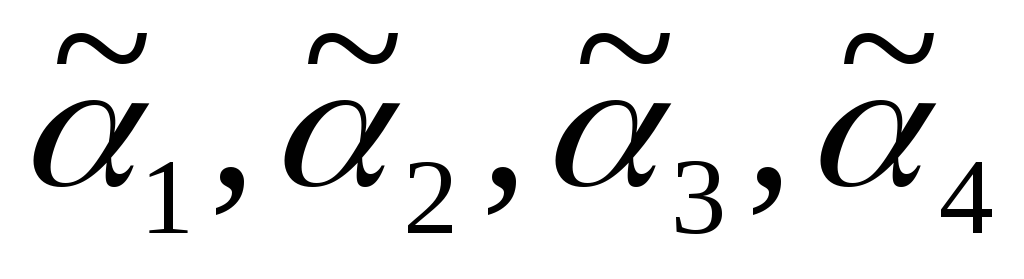

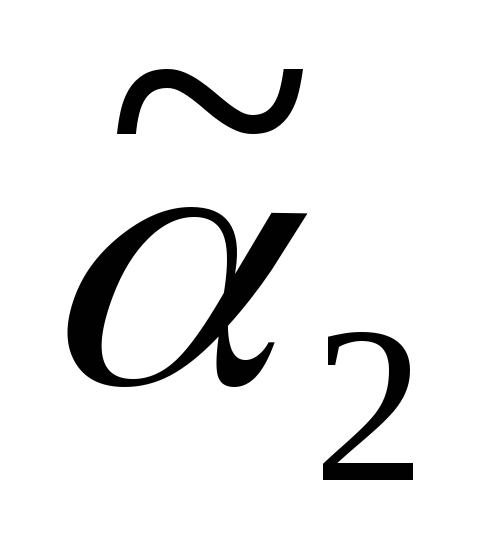
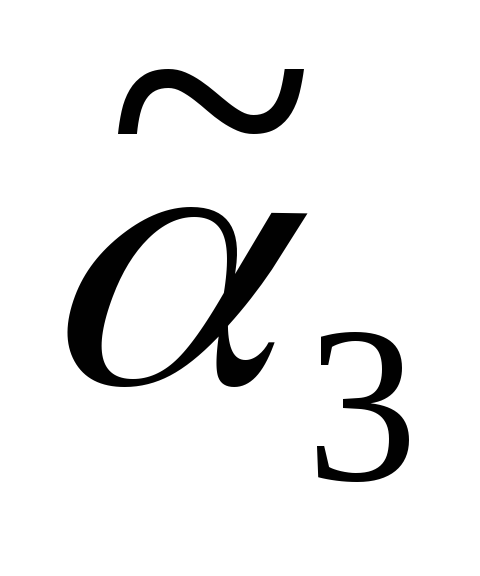
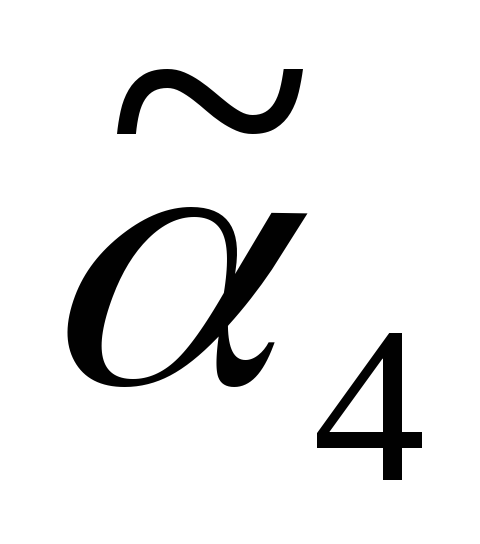
Источник
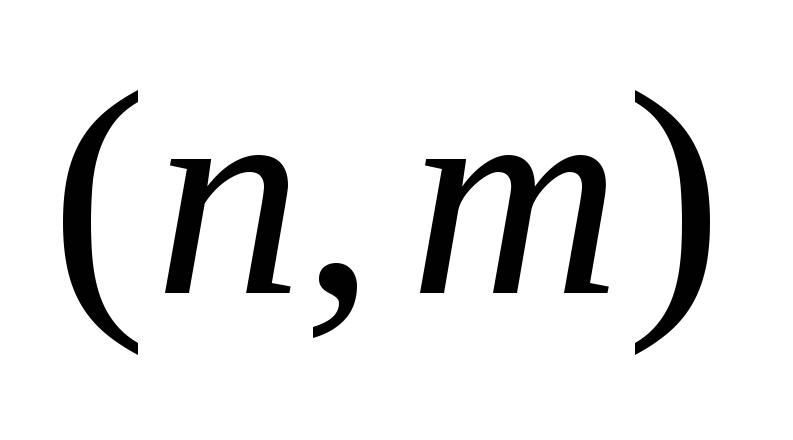 – графа
– графа  следующие утверждения эквивалентны:
следующие утверждения эквивалентны:  – дерево;
– дерево; соединяет единственная простая цепь;
соединяет единственная простая цепь; – связный граф, и любое ребро есть мост;
– связный граф, и любое ребро есть мост; – связный граф и древовидный;
– связный граф и древовидный; – ациклический граф (лес) и древовидный;
– ациклический граф (лес) и древовидный; – ациклический граф (лес) и субцикличекий;
– ациклический граф (лес) и субцикличекий; – связный, субциклический и неполный,
– связный, субциклический и неполный, 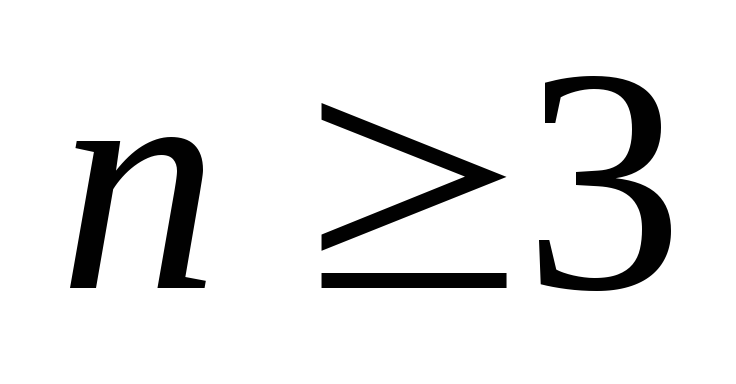 ;
; – древовидный и субциклический, исключая
– древовидный и субциклический, исключая 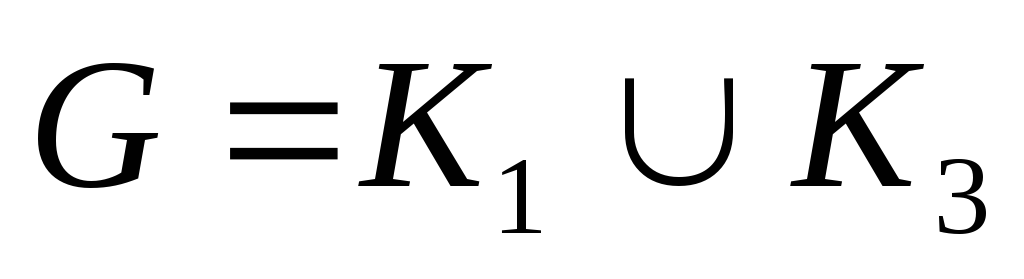 и
и 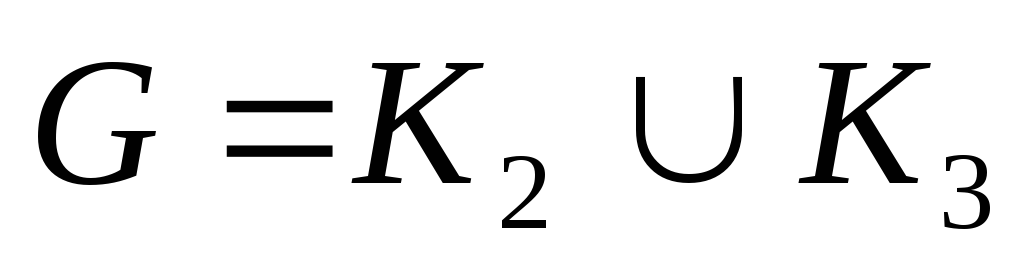 ;
;