Сжатие координат дерево отрезков

pakhomovee → Codeforces Round #893 (Div. 2) Editorial

K evin114514 → I’m Kevin114514, AMA!

itsvarsharma → Hello colours.

Error_Yuan → About #893 C

abcsumits → Help me to find number of solution of this equation efficiently

MikeMirzayanov → Изменение правил об использовании стороннего кода в соревнованиях Codeforces

T heQueenOfHatred → 2023 KSAAC Summer · solved.ac Arena #4 Announcement

Thaumic_Executor → Should CodeForces make the time of the contests more diverse?

Byakko → Invitation to 2023 USP Try-outs

Ibrahim-Elsayed → How to solve this problem?

JanBobi → How to block users in Codeforces

Rezwan.Arefin01 → Checklist for OI Problems (WebApp)

MikeMirzayanov → Codeforces Beta Round #9

awoo → Educational Codeforces Round 56 [рейтинговый для Div. 2]

lumibons → CEOI 2023

mohit_jx64 → [Invitation] Coding Events — Esya’23 IIIT-Delhi

MikeMirzayanov → Codeforces Beta Round #7

removed1 → Разбор задач Codeforces Beta Round #1

RAD → Codeforces Beta Round #22 (Див. 2)

e-maxx → Codeforces Beta Round #30. Разбор A

PinkieRabbit → AI language models and cheating in online contests

induk_v_tsiane → Codeforces Round #892 (Div. 2) Editorial

steveonalex → [Tutorial] Divide and Conquer Offline Query — A Niche Way to solve Static Range Query

RAD → Codeforces Round #113 (Div. 2) Разбор задач

MikeMirzayanov → Filter for Past Contests

Источник

Сжатое многомерное дерево отрезков

Вообще говоря, с поставленной задачей справится и обычное [math]p[/math] -мерное дерево отрезков. Для этого достаточно на [math]i[/math] -том уровне вложенности строить дерево отрезков по всевозможным [math]i[/math] -тым координатам точек множества [math]A[/math] , а при запросе использовать на каждом уровне бинарный поиск для установления желаемого подотрезка. Очевидно, запрос будет делаться за [math]O(\log^p\,n)[/math] времени, а сама структура данных будет занимать [math]O(n^p)[/math] памяти.

Оптимизация

Для уменьшения количества занимаемой памяти можно провести оптимизацию [math]p[/math] -мерного дерева отрезков. Для начала, будем использовать дерево отрезков с сохранением всего подотрезка в каждой вершине. Другими словами, в каждой вершине дерева отрезков мы будем хранить не только какую-то сжатую информацию об этом подотрезке, но и все элементы множества [math]A[/math] , лежащие в этом подотрезке. На первый взгляд, это только увеличит объем структуры, но не все так просто. При построении будем действовать следующим образом — каждый раз дерево отрезков внутри вершины будем строить не по всем элементам множества [math]A[/math] , а только по сохраненному в этой вершине подотрезку. Действительно, незачем строить дерево по всем элементам, когда элементы вне подотрезка уже были «исключены» и заведомо лежат вне желаемого [math]p[/math] -мерного прямоугольника. Такое «усеченное» многомерное дерево отрезков называется сжатым (англ. compressed).

Построение дерева

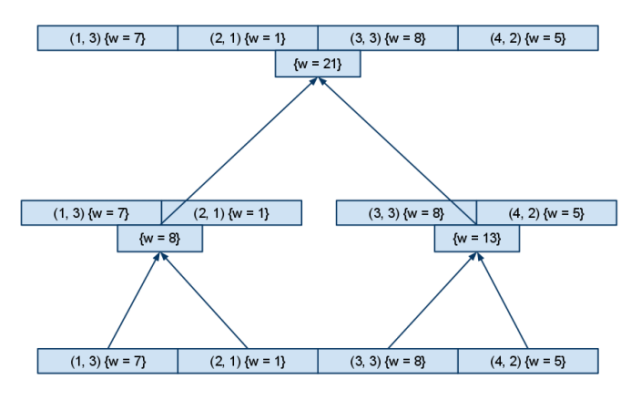
Рассмотрим алгоритм построения сжатого дерева отрезков на примере множества [math]A[/math] , состоящего из [math]4[/math] -х взвешенных точек в [math]2[/math] -мерном пространстве (плоскости):

Cоставим массив из всех [math]n[/math] элементов множества [math]A[/math] , упорядочим его по первой координате, построим на нём дерево отрезков с сохранением подмассива в каждой вершине

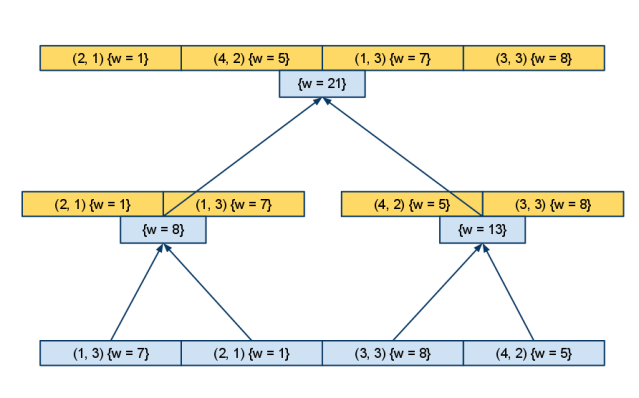
Все подмассивы в вершинах получившегося дерева отрезков упорядочим по следующей координате

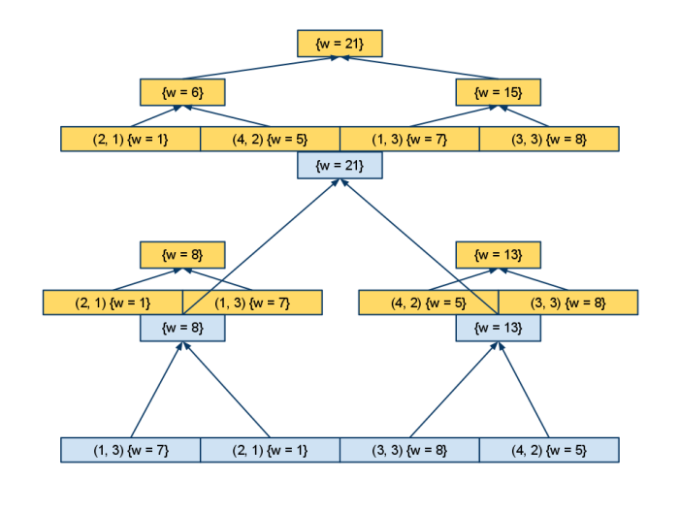
Повторим построение дерева для каждого из них (координата последняя, поэтому в вершинах этих деревьев мы уже ничего строить не будем — подмассивы в каждой вершине можно не сохранять)

Псевдокод

buildSubarrayTree(element[] array): // построение одномерного дерева отрезков на массиве array с сохранением подмассива в каждой вершине buildNormalTree(element[] array): // построение обычного одномерного дерева отрезков на массиве array getInsideArray(vertex v): // получение подмассива, сохраненного в вершине vertex buildCompressedTree(element[] array, int coordinate = 1): // рекурсивная процедура построения сжатого дерева отрезков if coordinate < p sort(array, coordinate) // сортировка массива по нужной координате segmentTree = buildSubarrayTree(array); foreach v: vertex in segmentTree buildCompressedTree(getInsideArray(v), coordinate + 1); if coordinate == p sort(array, coordinate) buildNormalTree(array);

Анализ полученной структуры

Легко понять, что сжатое [math]p[/math] -мерное дерево отрезков будет занимать [math]O(n\log^\,n)[/math] памяти: превращение обычного дерева в дерево с сохранением всего подотрезка в каждой вершине будет увеличивать его размер в [math]O(\log\,n)[/math] раз, а сделать это нужно будет [math]p-1[/math] раз. Но расплатой станет невозможность делать произвольный запрос модификации: в самом деле, если появится новый элемент, то это приведёт к тому, что мы должны будем в каком-либо дереве отрезков по второй или более координате добавить новый элемент в середину, что эффективно сделать невозможно. Что касается запроса веса, он будет полностью аналогичен запросу в обычном [math]p[/math] -мерном дереве отрезков за [math]O(\log^p\,n)[/math] .

См. также

Источники информации

Источник

Дерево отрезков

Дерево отрезков — очень мощная и гибкая структура данных, позволяющая быстро отвечать на самые разные запросы на отрезках.

Рассмотрим конкретную задачу: дан массив $a$ из $n$ целых чисел, и требуется отвечать на запросы двух типов:

Изменить значение в ячейке (т. е. реагировать на присвоение a[k] = x ).
Вывести сумму элементов $a_i$ на отрезке с $l$ по $r$.

Оба запроса нужно обрабатывать за время $O(\log n)$.

Структура дерева отрезков

Чтобы решить задачу, сделаем с исходным массивом следующие манипуляции.

Посчитаем сумму всего массива и где-нибудь запишем. Потом разделим его пополам, посчитаем сумму на половинах и тоже где-нибудь запишем. Каждую половину потом разделим пополам ещё раз, и так далее, пока не придём к отрезкам длины 1.

Эту последовательность разбиений можно представить в виде дерева.

Корень этого дерева соответствует отрезку $[0, n)$, а каждая вершина (не считая листьев) имеет ровно двух сыновей, которые тоже соответствуют каким-то отрезкам. Отсюда и название — «дерево отрезков».

Разные полезные свойства

Высота дерева отрезков равна $\Theta(\log n)$: на каждом новом уровне длина отрезка уменьшается вдвое. Этот факт будет ключевым для оценки асимптотики операций.

Любой полуинтервал разбивается на $O(\log n)$ неперекрывающихся полуинтервалов, соответствующих в вершинам дерева: с каждого уровня нам достаточно не более двух отрезков.

Дерево содержит менее $2n$ вершин: первый уровень дерева отрезков содержит одну вершину (корень), второй уровень — в худшем случае две вершины, на третьем уровне в худшем случае будет четыре вершины, и так далее, пока число вершин не достигнет $n$. Таким образом, число вершин в худшем случае оценивается суммой $n + \frac + \frac + \frac + \ldots + 1 < 2n$. Значит, оно линейное по памяти.

При $n$, отличных от степеней двойки, не все уровни дерева отрезков будут полностью заполнены. Например, при $n=3$ левый сын корня есть отрезок $[0, 2)$, имеющий двух потомков, в то время как правый сын корня — отрезок $[2, 3)$, являющийся листом.

Ок, как это нам поможет?

Опишем, как с помощью такой структуры решить исходную задачу.

Запрос обновления. Нам нужно обновить значения в вершинах таким образом, чтобы они соответствовали новому значению $a[k] = x$.

Изменим все вершины, в суммах которых участвует $k$-тый элемент. Их будет $\Theta(\log n)$ — по одной с каждого уровня.

Это можно реализовать как рекурсивную функцию: ей передаётся текущая вершина дерева отрезков, и функция выполняет рекурсивный вызов от одного из двух своих сыновей (от того, который содержит $k$-ый элемент в своём отрезке), а после этого — пересчитывает значение суммы в текущей вершине точно таким же образом, как мы это делали при построении дерева отрезков.

Запрос суммы. Мы знаем, что во всех вершинах лежат корректные значения, и нам с помощью них посчитать сумму на отрезке.

Сделаем тоже рекурсивную функцию, рассмотрев три случая:

Если отрезок вершины лежит целиком в отрезке запроса, то вернуть записанную в ней сумму.
Если отрезки вершины и запроса не пересекаются, то вернуть 0.
Иначе разделиться рекурсивно на 2 половины и вернуть сумму этой функции от обоих детей.

Чтобы разобраться, почему это работает за $O(\log n)$, нужно оценить количество «интересных» отрезков — тех, которые порождают новые вызовы рекурсии. Это будут только те, которые содержат границу запросов — остальные сразу завершатся. Обе границы отрезка содержатся в $O(\log n)$ отрезках, а значит и итоговая асимптотика будет такая же.

Дерево отрезков можно использовать для гораздо большего, чем только для суммы.

Далее этой главе мы рассмотрим разные реализации и варианты этой структуры и их применения.

Источник