Теория графов
Следующая теорема устанавливает, что два из четырех свойств – связность, ацикличность, древовидность и субцикличность – характеризуют граф как дерево.
- Для
– графа
следующие утверждения эквивалентны:
– дерево;
- Любые две несовпадающие вершины графа
соединяет единственная простая цепь;
– связный граф, и любое ребро есть мост;
– связный граф и древовидный;
– ациклический граф (лес) и древовидный;
– ациклический граф (лес) и субцикличекий;
– связный, субциклический и неполный,
;
– древовидный и субциклический, исключая
и
;
- (1->2): Если
-
Ориентированные деревья
- Ориентированным деревом (или ордеревом, или корневым деревом) называется орграф со следующими свойствами:
- существует единственный узел, в который не входит ни один другой узел. Он называется корнем ордерева;
- во все остальные узлы входит только по одному узлу;
- каждый узел достижим из корня.
- Ордерево обладает следующими свойствами:
- Концевая вершина ордерева называется листом. Путь из корня в лист называется ветвью. Длина наибольшей ветви ордерева называется высотой. Уровень узла ордерева – это расстояние отт корня до узла. Сам корень имеет уровень 0. Узлы одного уровня образуют ярус дерева.
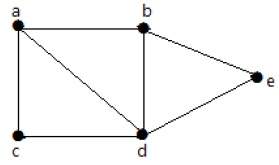
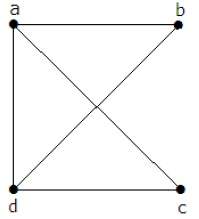
 – дерево, то любые две его несовпадающие вершины соединяет единственная простая цепь. От противного. Пусть существуют две цепи
– дерево, то любые две его несовпадающие вершины соединяет единственная простая цепь. От противного. Пусть существуют две цепи 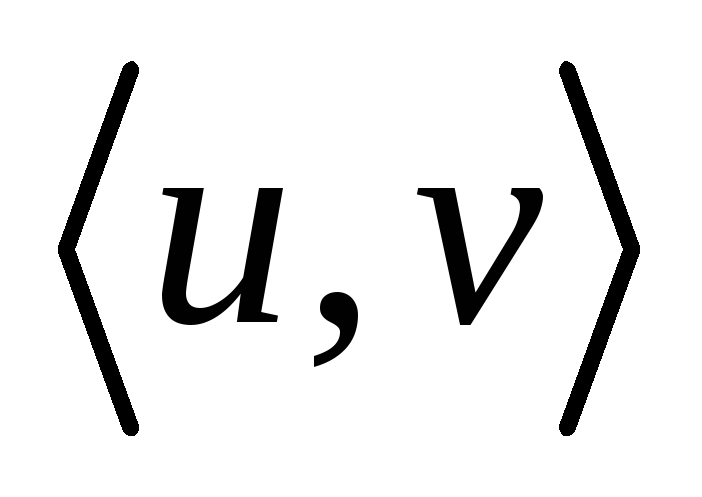 (см. рис.).
(см. рис.).  Тогда
Тогда 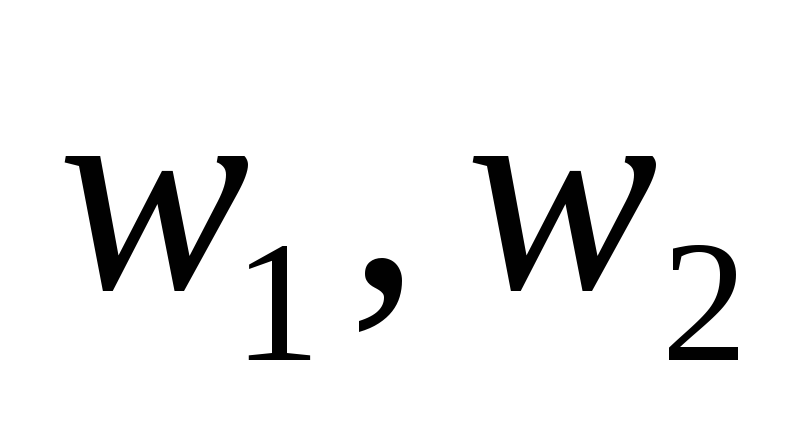 — простой цикл. (2->3): Если любые две несовпадающие вершины графа
— простой цикл. (2->3): Если любые две несовпадающие вершины графа  соединяет единственная простая цепь, то
соединяет единственная простая цепь, то  – связный граф, и любое ребро есть мост. Имеем:
– связный граф, и любое ребро есть мост. Имеем: 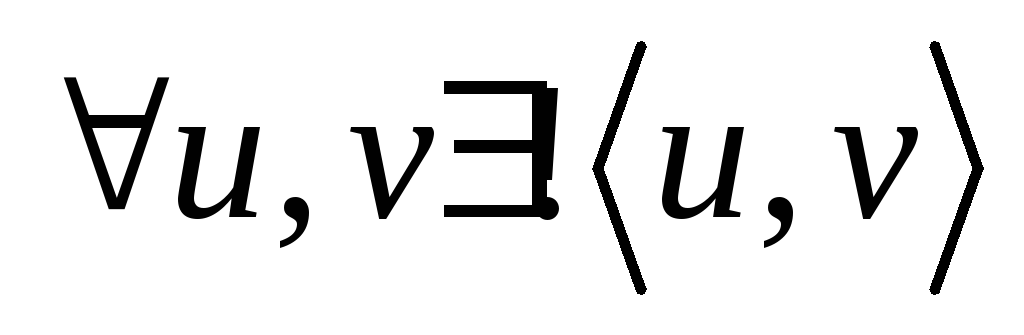

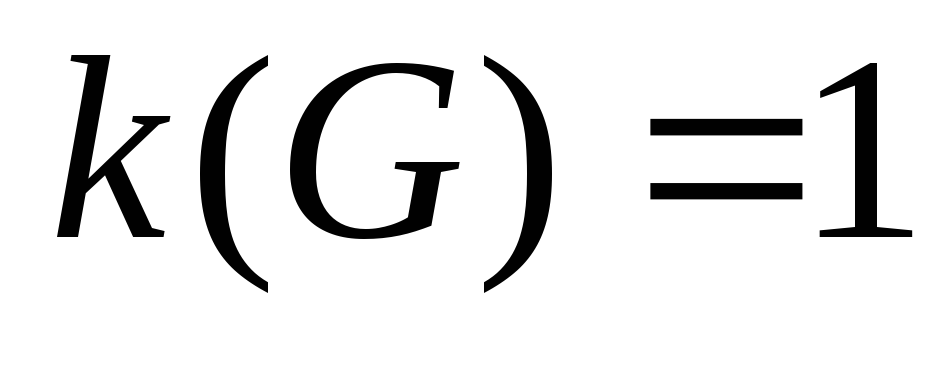 (число компонент связности). Далее от противного. Пусть ребро
(число компонент связности). Далее от противного. Пусть ребро 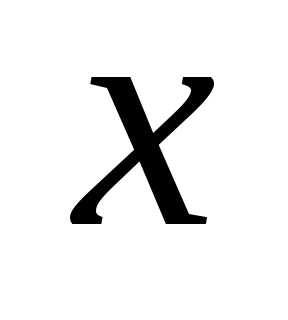 — не мост. Тогда в
— не мост. Тогда в 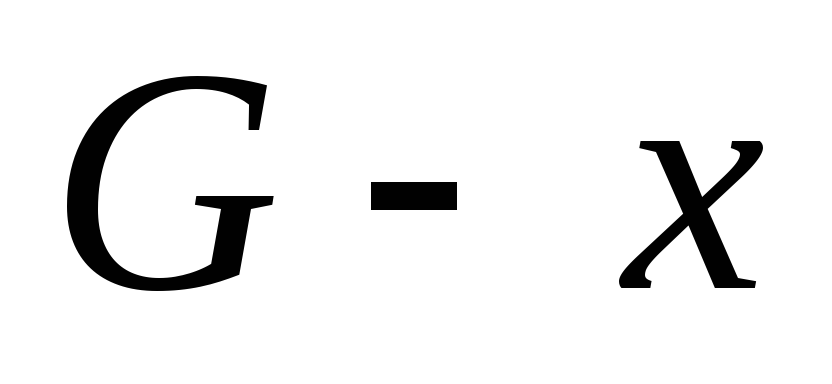 концы этого ребра связаны цепью. Само ребро
концы этого ребра связаны цепью. Само ребро 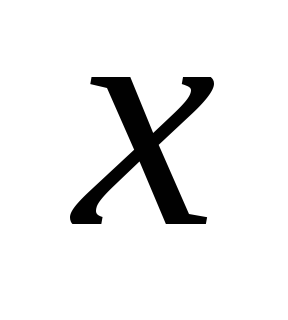 в исходном графе – вторая цепь, что противоречит условию. (3->4): Если
в исходном графе – вторая цепь, что противоречит условию. (3->4): Если  – связный граф, и любое ребро есть мост, то
– связный граф, и любое ребро есть мост, то  – связный и древовидный (
– связный и древовидный (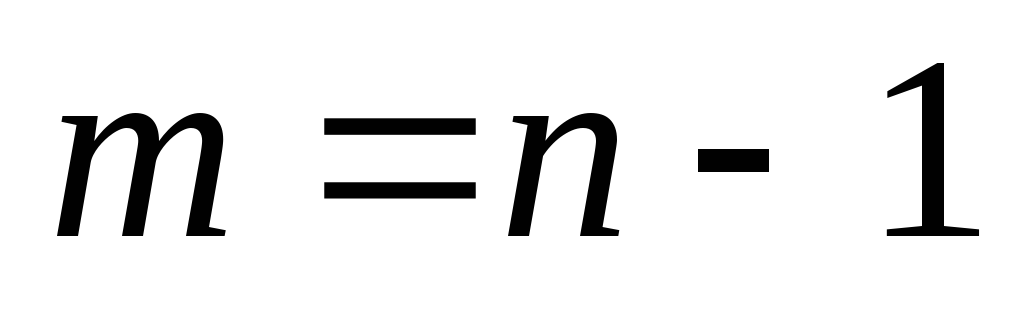 ). Индукция по
). Индукция по 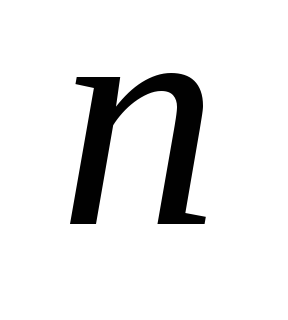 (числу вершин). Если
(числу вершин). Если 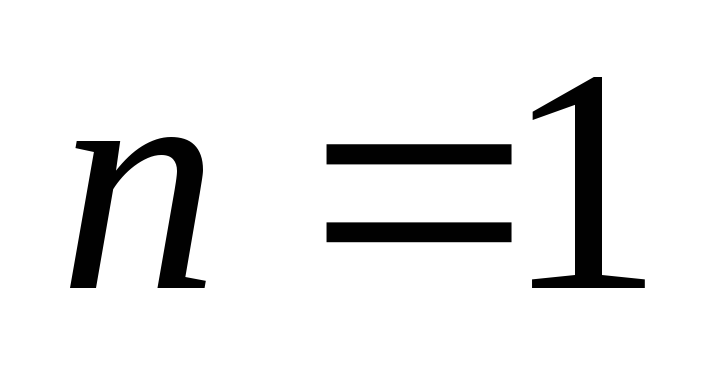 , то
, то 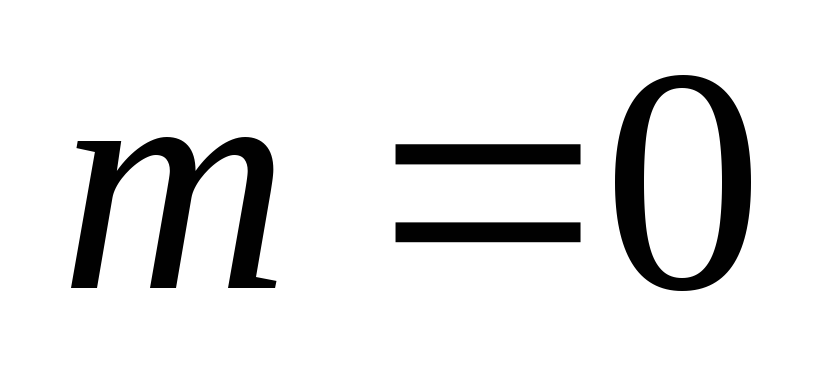 (число ребер). Пусть равенство
(число ребер). Пусть равенство 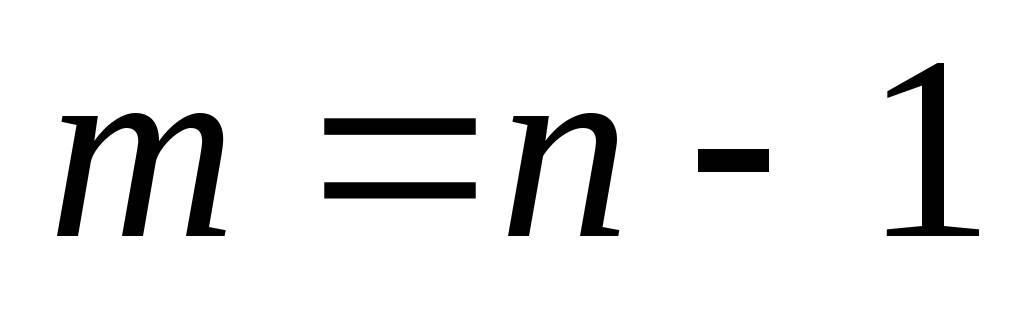 выполняется для всех графов
выполняется для всех графов  с числом вершин меньше
с числом вершин меньше 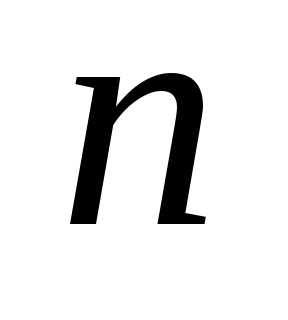 . Докажем, что оно выполняется и для
. Докажем, что оно выполняется и для 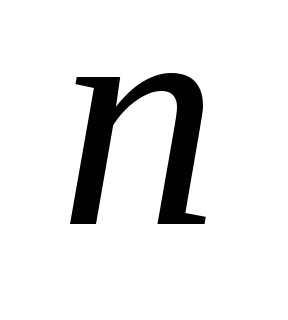 вершин. Удалим из
вершин. Удалим из  ребро
ребро 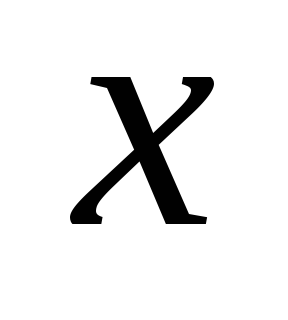 , являющееся мостом. Получим две компоненты связности
, являющееся мостом. Получим две компоненты связности  и
и  , для которых верно равенство
, для которых верно равенство 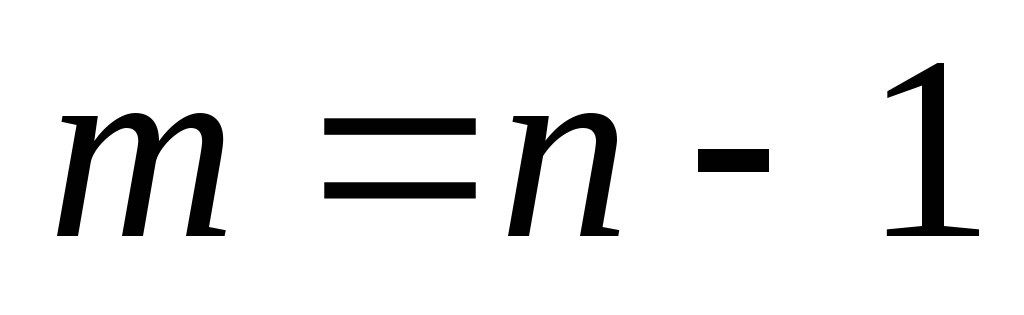 . Т.е.
. Т.е. 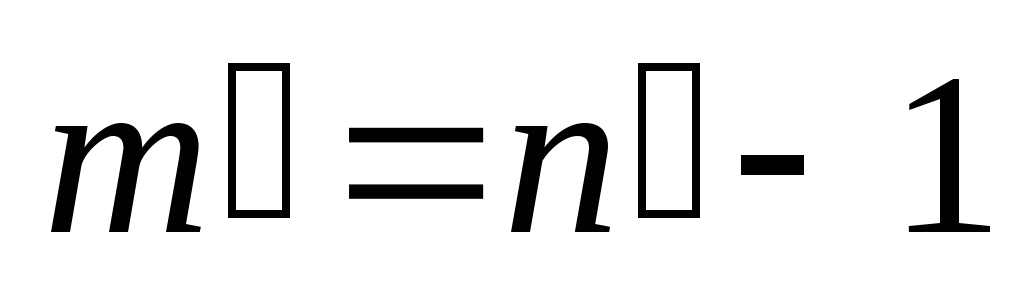 ,
, 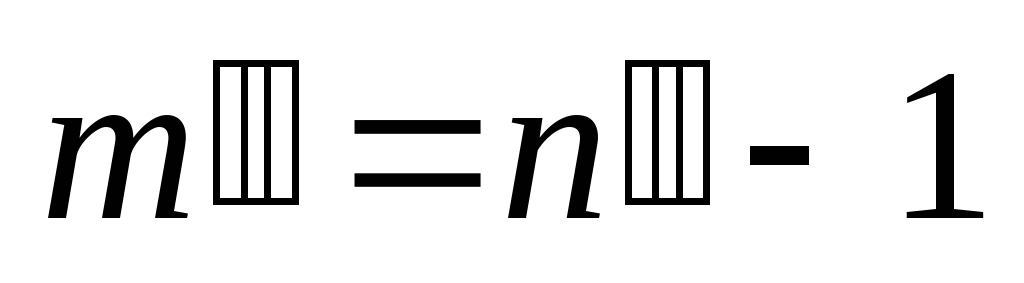 . Тогда
. Тогда  . (4->5): Если
. (4->5): Если  – связный и древовидный (
– связный и древовидный (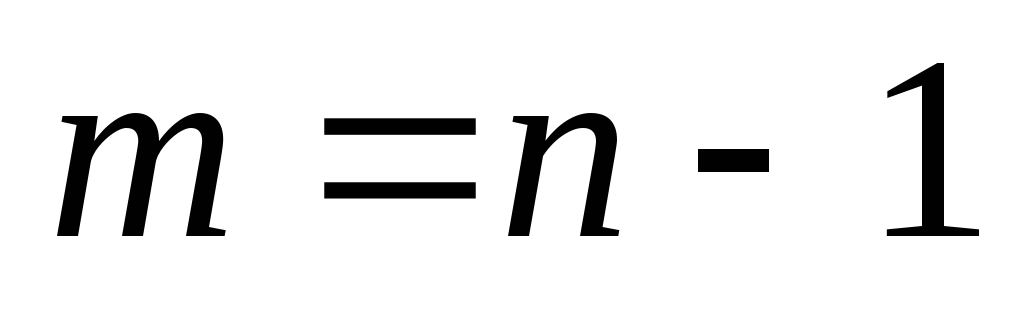 ), то
), то  – ациклический граф (лес) и древовидный (
– ациклический граф (лес) и древовидный (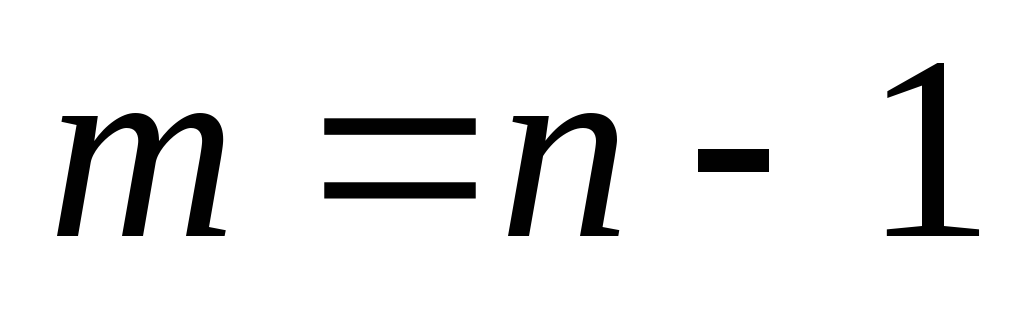 ). От противного. Пусть есть цикл с
). От противного. Пусть есть цикл с 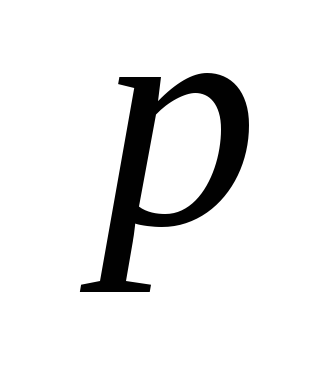 вершинами и
вершинами и  ребрами. Остальные
ребрами. Остальные 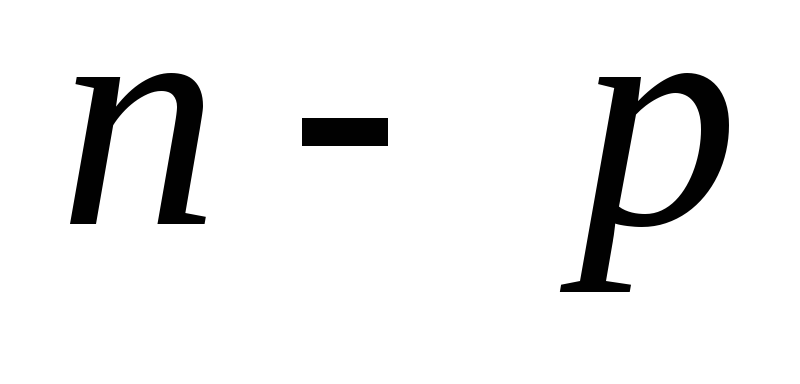 вершин связаны с этим циклом ребрами, т.к. граф связный. Следовательно,
вершин связаны с этим циклом ребрами, т.к. граф связный. Следовательно, 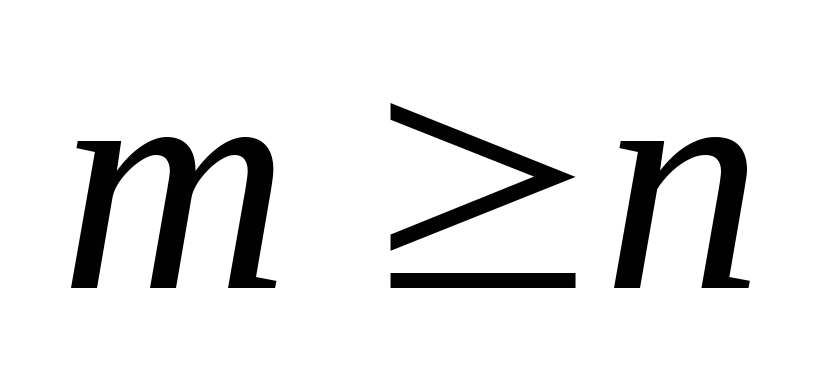 , что противоречит условию
, что противоречит условию 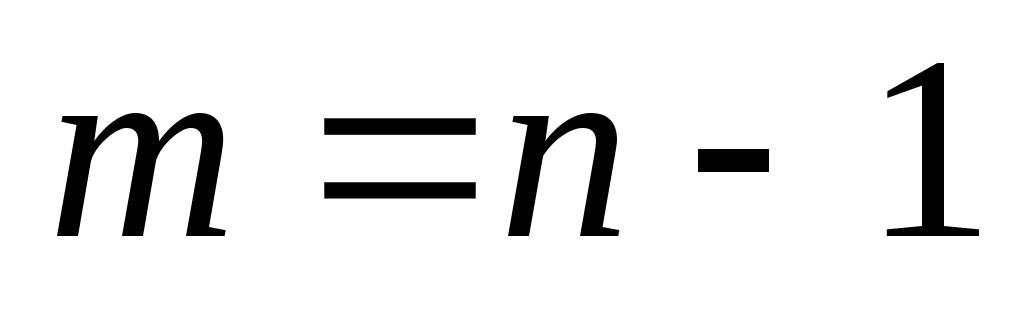 . Остальное без док-ва.
. Остальное без док-ва. 1. 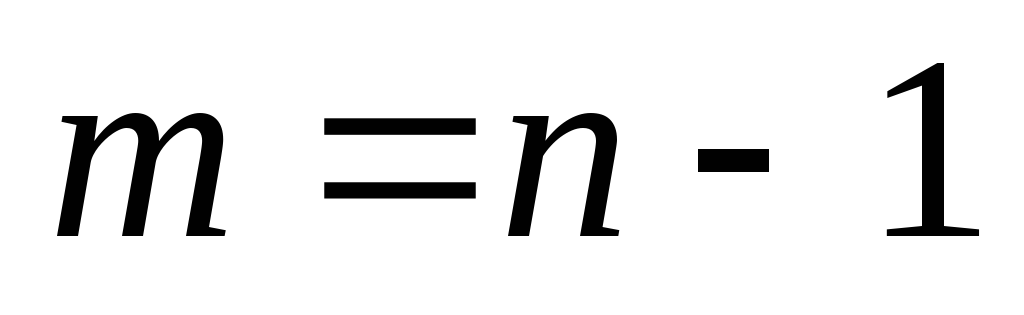
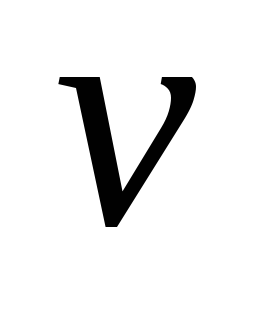
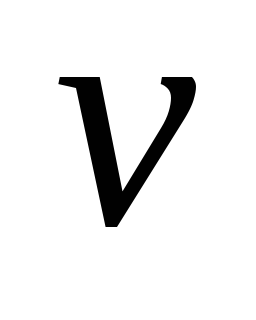
Источник
Теория графов – деревья
Деревья – это графики, которые не содержат ни одного цикла. Они представляют иерархическую структуру в графической форме. Деревья относятся к простейшему классу графов. Несмотря на их простоту, они имеют богатую структуру.
Деревья предоставляют целый ряд полезных приложений, от простого семейного дерева до сложных в структурах данных компьютерной науки.
дерево
Связный ациклический граф называется деревом. Другими словами, связный граф без циклов называется деревом.
Края дерева известны как ветви . Элементы деревьев называются их узлами . Узлы без дочерних узлов называются листовыми узлами .
Дерево с ‘n’ вершинами имеет ‘n-1’ ребер. Если у него есть еще одно ребро, превышающее ‘n-1’, то это дополнительное ребро, очевидно, должно соединиться с двумя вершинами, что приводит к образованию цикла. Затем он становится циклическим графом, что является нарушением для графа дерева.
Пример 1
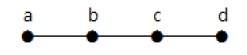
График, показанный здесь, является деревом, потому что у него нет циклов, и он связан. Он имеет четыре вершины и три ребра, т. Е. Для ‘n’ вершин ‘n-1’ ребер, как указано в определении.
Примечание. Каждое дерево имеет как минимум две вершины первой степени.
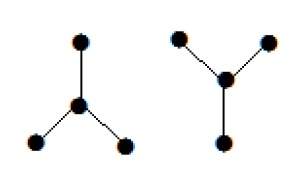
Пример 2
В приведенном выше примере вершины «a» и «d» имеют степень один. А две другие вершины ‘b’ и ‘c’ имеют второй уровень. Это возможно, потому что для того, чтобы не формировать цикл, в диаграмме должно быть как минимум два отдельных ребра. Это не что иное, как два ребра со степенью один.
лес
Несвязный ациклический граф называется лесом. Другими словами, непересекающаяся коллекция деревьев называется лесом.
пример
Следующий график выглядит как два подграфа; но это один несвязный граф. На этом графике нет циклов. Отсюда ясно, что это лес.
Охватывающие деревья
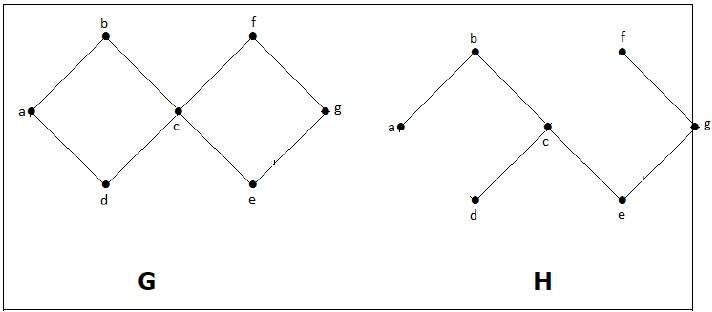
Пусть G – связный граф, тогда подграф H в G называется остовным деревом в G, если –
Остовное дерево T неориентированного графа G является подграфом, который включает в себя все вершины G.
пример
В приведенном выше примере G является связным графом, а H является подграфом G.
Ясно, что граф H не имеет циклов, это дерево с шестью ребрами, которое на единицу меньше общего числа вершин. Следовательно, H – остовное дерево группы G.
Circuit Rank
Пусть «G» связный граф с «n» вершинами и «m» ребрами. Остовное дерево ‘T’ группы G содержит (n-1) ребер.
Следовательно, количество ребер, которые нужно удалить из ‘G’, чтобы получить остовное дерево = m- (n-1), которое называется рангом схемы G.
Эта формула верна, потому что в остовном дереве вам нужно иметь ребра n-1. Из «m» ребер вам нужно сохранить «n – 1» ребер в графе.
Следовательно, удаление ребер n – 1 из m дает ребра, которые нужно удалить из графа, чтобы получить остовное дерево, которое не должно образовывать цикл.
пример
Посмотрите на следующий график –
Для графика, приведенного в примере выше, у вас есть m = 7 ребер и n = 5 вершин.
пример
Пусть ‘G’ – связный граф с шестью вершинами, а степень каждой вершины равна трем. Найдите звание цепи «G».
По сумме теоремы о степени вершин
Теорема Кирхгофа
Теорема Кирхгофа полезна для нахождения числа связующих деревьев, которые могут быть сформированы из связного графа.
пример
Матрица «А» заполняется так, как если между двумя вершинами есть ребро, то она должна быть задана как «1», иначе «0».
Источник
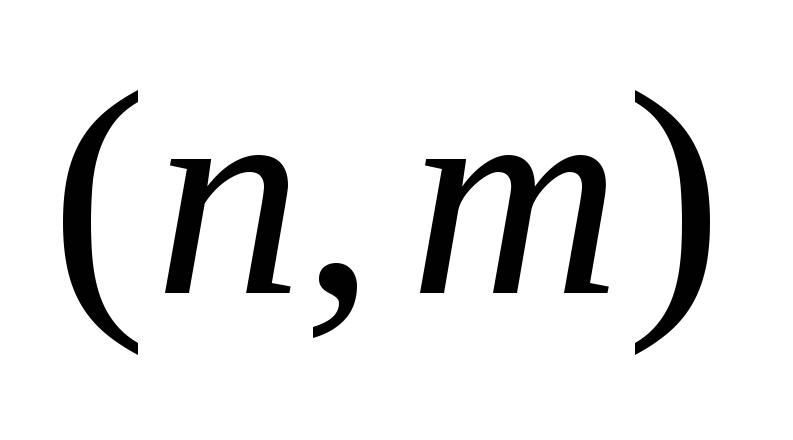 – графа
– графа  следующие утверждения эквивалентны:
следующие утверждения эквивалентны:  – дерево;
– дерево; соединяет единственная простая цепь;
соединяет единственная простая цепь; – связный граф, и любое ребро есть мост;
– связный граф, и любое ребро есть мост; – связный граф и древовидный;
– связный граф и древовидный; – ациклический граф (лес) и древовидный;
– ациклический граф (лес) и древовидный; – ациклический граф (лес) и субцикличекий;
– ациклический граф (лес) и субцикличекий; – связный, субциклический и неполный,
– связный, субциклический и неполный, 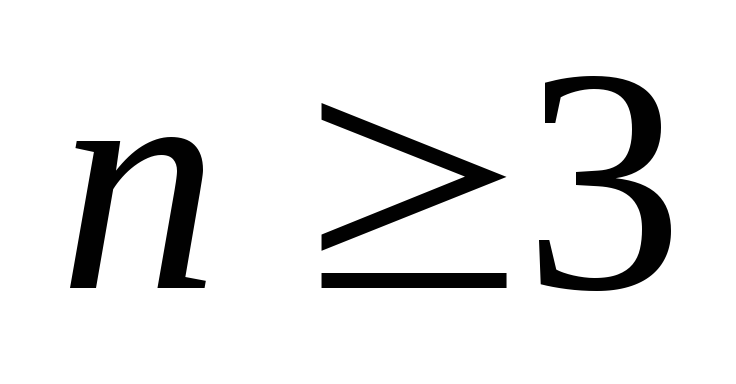 ;
; – древовидный и субциклический, исключая
– древовидный и субциклический, исключая 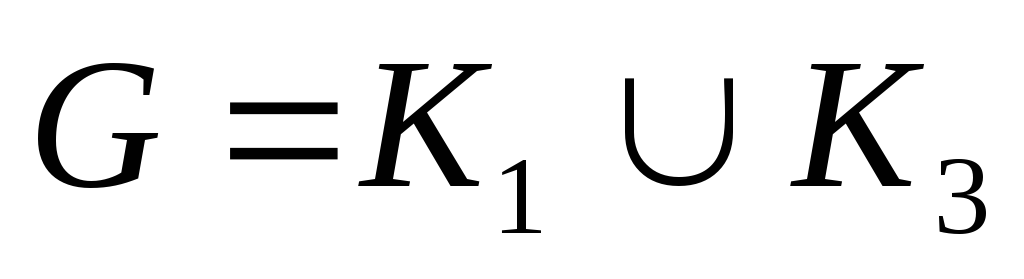 и
и 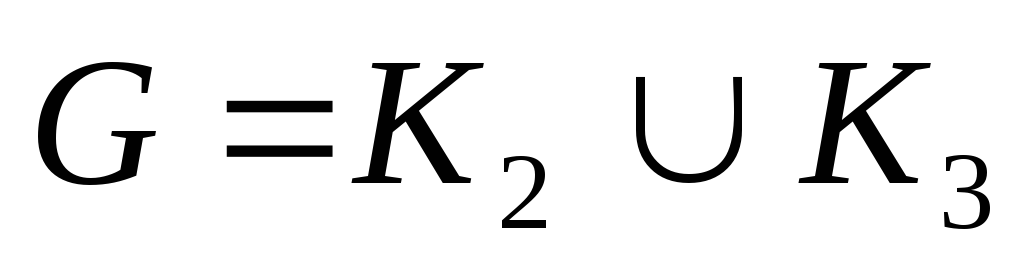 ;
;