Теория графов построение дерева

Теория графов – деревья

Деревья – это графики, которые не содержат ни одного цикла. Они представляют иерархическую структуру в графической форме. Деревья относятся к простейшему классу графов. Несмотря на их простоту, они имеют богатую структуру.

Деревья предоставляют целый ряд полезных приложений, от простого семейного дерева до сложных в структурах данных компьютерной науки.

дерево

Связный ациклический граф называется деревом. Другими словами, связный граф без циклов называется деревом.

Края дерева известны как ветви . Элементы деревьев называются их узлами . Узлы без дочерних узлов называются листовыми узлами .

Дерево с ‘n’ вершинами имеет ‘n-1’ ребер. Если у него есть еще одно ребро, превышающее ‘n-1’, то это дополнительное ребро, очевидно, должно соединиться с двумя вершинами, что приводит к образованию цикла. Затем он становится циклическим графом, что является нарушением для графа дерева.

Пример 1

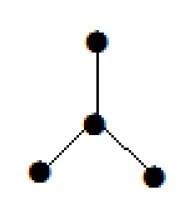
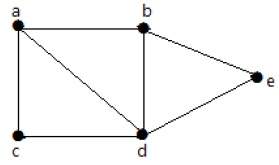
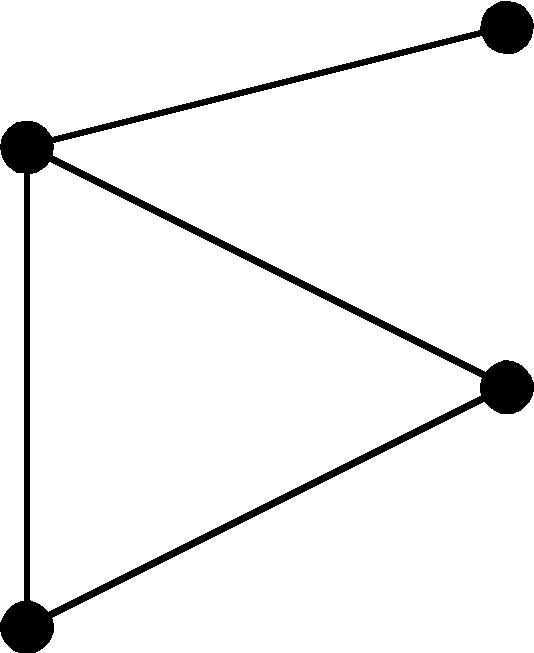
График, показанный здесь, является деревом, потому что у него нет циклов, и он связан. Он имеет четыре вершины и три ребра, т. Е. Для ‘n’ вершин ‘n-1’ ребер, как указано в определении.

Примечание. Каждое дерево имеет как минимум две вершины первой степени.

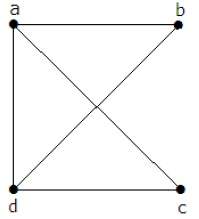
Пример 2

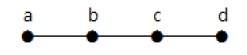
В приведенном выше примере вершины «a» и «d» имеют степень один. А две другие вершины ‘b’ и ‘c’ имеют второй уровень. Это возможно, потому что для того, чтобы не формировать цикл, в диаграмме должно быть как минимум два отдельных ребра. Это не что иное, как два ребра со степенью один.

лес

Несвязный ациклический граф называется лесом. Другими словами, непересекающаяся коллекция деревьев называется лесом.

пример

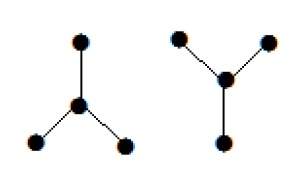
Следующий график выглядит как два подграфа; но это один несвязный граф. На этом графике нет циклов. Отсюда ясно, что это лес.

Охватывающие деревья

Пусть G – связный граф, тогда подграф H в G называется остовным деревом в G, если –

Остовное дерево T неориентированного графа G является подграфом, который включает в себя все вершины G.

пример

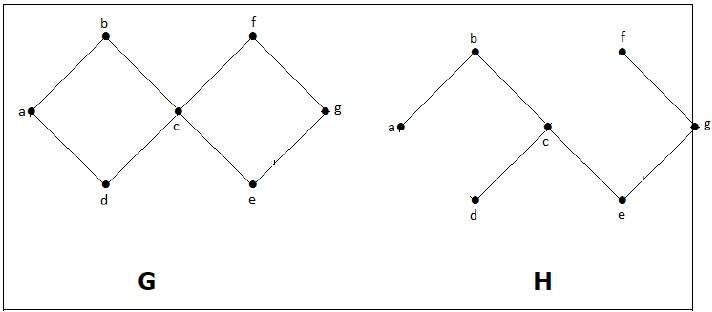
В приведенном выше примере G является связным графом, а H является подграфом G.

Ясно, что граф H не имеет циклов, это дерево с шестью ребрами, которое на единицу меньше общего числа вершин. Следовательно, H – остовное дерево группы G.

Circuit Rank

Пусть «G» связный граф с «n» вершинами и «m» ребрами. Остовное дерево ‘T’ группы G содержит (n-1) ребер.

Следовательно, количество ребер, которые нужно удалить из ‘G’, чтобы получить остовное дерево = m- (n-1), которое называется рангом схемы G.

Эта формула верна, потому что в остовном дереве вам нужно иметь ребра n-1. Из «m» ребер вам нужно сохранить «n – 1» ребер в графе.

Следовательно, удаление ребер n – 1 из m дает ребра, которые нужно удалить из графа, чтобы получить остовное дерево, которое не должно образовывать цикл.

пример

Посмотрите на следующий график –

Для графика, приведенного в примере выше, у вас есть m = 7 ребер и n = 5 вершин.

пример

Пусть ‘G’ – связный граф с шестью вершинами, а степень каждой вершины равна трем. Найдите звание цепи «G».

По сумме теоремы о степени вершин

Теорема Кирхгофа

Теорема Кирхгофа полезна для нахождения числа связующих деревьев, которые могут быть сформированы из связного графа.

пример

Матрица «А» заполняется так, как если между двумя вершинами есть ребро, то она должна быть задана как «1», иначе «0».

Источник

8. Остовы и деревья

Понятие дерева широко используется во многих областях математики и информатики. Например, как инструмент при вычислениях, как удобный способ хранения данных, способ сортировки или поиска данных.

Достаточно развитое генеалогическое дерево образует дерево.

Типичное частичное организационное дерево для университета.

Если дерево имеет хотя бы одно ребро, оно имеет две вершины со степенью 1. Вершины со степенью 1 называются листьями. Другие вершины называются внутренними вершинами.

Предположим, что дерево представляет физический объект, подвижный в вершинах, и подвесим дерево за одну из его вершин:

Если подвесить за вершину V3 или V4

Вершина в верхней части называется корнем дерева, если корень определен, то дерево называется корневым. При необходимости корневое дерево Т можно заменить на ориентированное корневое дерево Т’, порожденное корневым деревом Т.

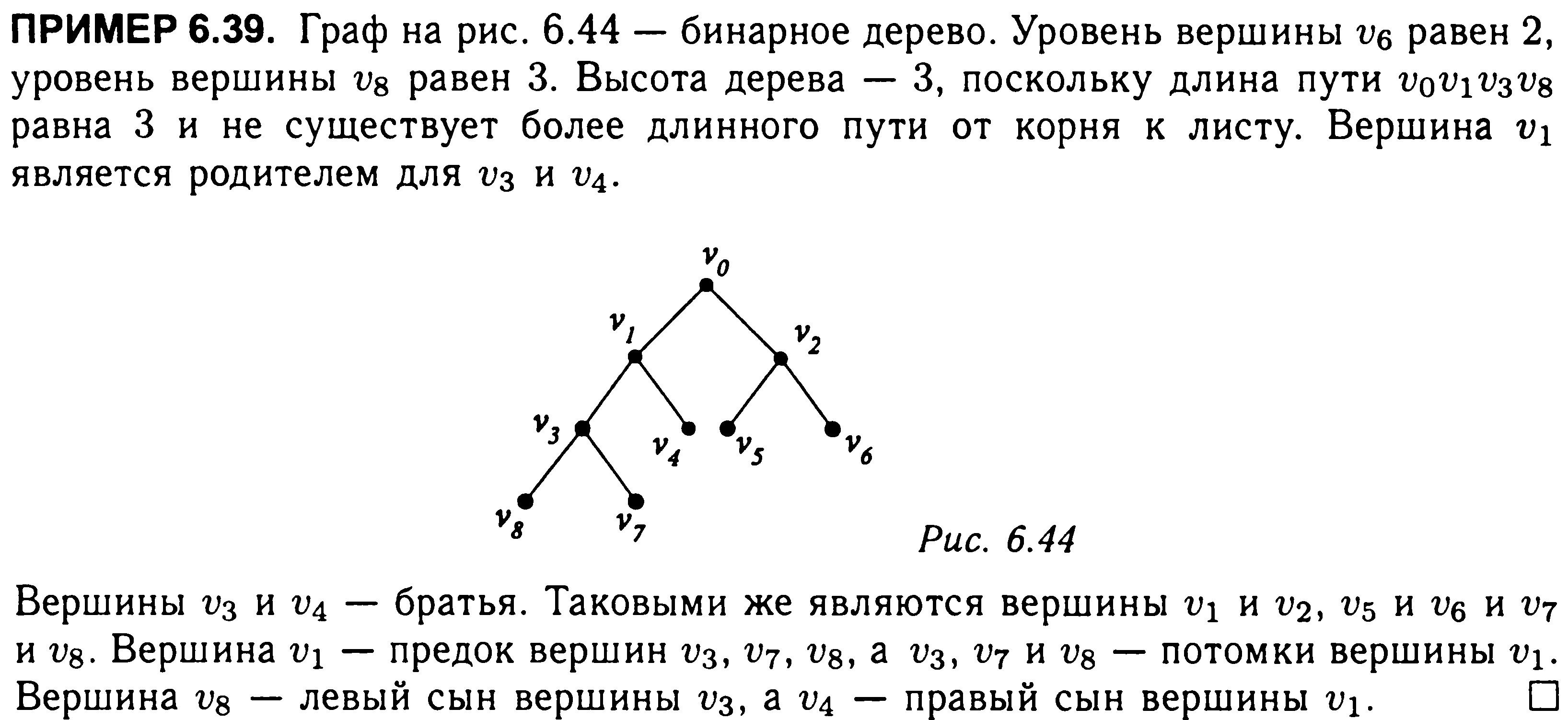
Если корень выбран, уровень вершины V определяется длиной единственного пути из корня в вершину V. Высотой дерева называется длина самого длинного пути от корня дерева до листа.

Если рассматривается корневое ориентированное дерево Т’, порожденное данным корневым деревом Т, тогда вершина u называется родителем вершины v; a v называется сыном вершины u, если существует ориентированное ребро из u в v.

Если u — родитель v и v1, тогда v и v1 называются братьями.

Если существует ориентированный путь из вершины u в вершину v, тогда u называется предком вершины v, a v называется потомком вершины u.

Если наибольшая из степеней выхода для вершин дерева равна m, тогда дерево называется m — арным деревом.

В частном случае, когда m = 2, дерево называется бинарным деревом.

В каждом бинарном дереве каждый сын родителя обозначается либо как левый сын, либо как правый сын (но не то и другое одновременно).

Связный граф G(V,E), не имеющий циклов, называется деревом.

ТЕОРЕМА (основные свойства деревьев):

Пусть граф G(V,E) имеет n вершин. Тогда следующие утверждения эквивалентны:

1. G является деревом;
2. G не содержит циклов и имеет n-1 рёбер;
3. G связен и имеет n-1 рёбер;
4. G связен, но удаление » ребра нарушает связность;
5. » две вершины графа G соединены ровно одним путём;
6. G не имеет циклов, но добавление » ребра порождает ровно один цикл.

Ориентированное дерево представляет собой ориентированный граф без циклов, в котором полустепень захода каждой вершины (за исключением одной, например v₁) не больше 1, а полустепень захода вершины v₁ (называемой также корнем) равна нулю. Вершину v ордерева называют потомком вершины u, если $ путь из u в v. В этом же случае вершину u называют предком вершины v. Вершину, не имеющую потомков, называют листом. 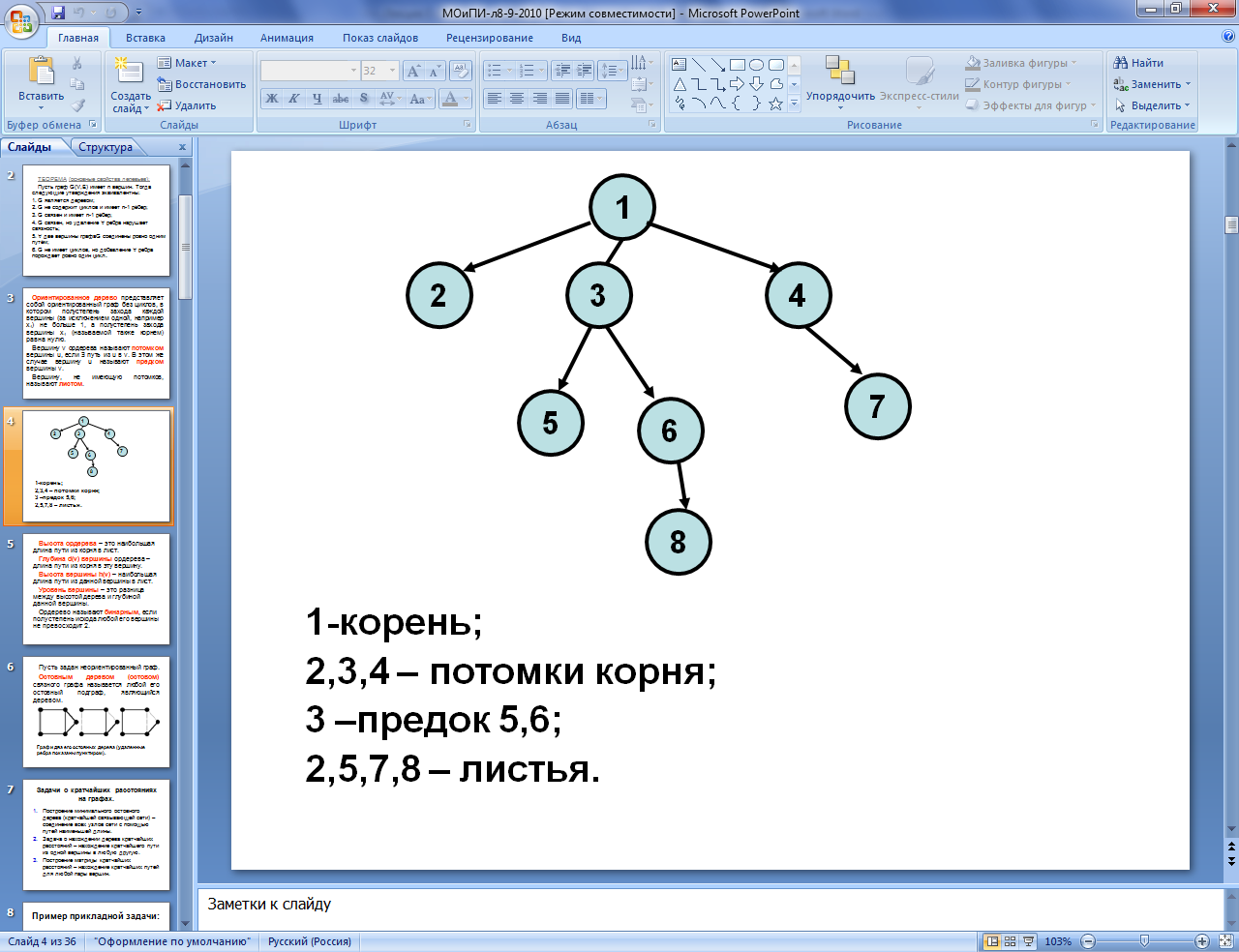Высота ордерева – это наибольшая длина пути из корня в лист. Уровень вершины ордерева – длина пути из корня в эту вершину. Ордерево называют бинарным, если полустепень исхода любой его вершины не превосходит 2. Пусть задан неориентированный граф. Остовным деревом (остовом) связного графа называется любой его остовный подграф, являющийся деревом. Граф и два его остовных дерева (удаленные ребра показаны пунктиром).Задачи о кратчайших расстояниях на графах.

1. Построение минимального остовного дерева (кратчайшей связывающей сети) – соединение всех узлов сети с помощью путей наименьшей длины.
2. Задача о нахождении дерева кратчайших расстояний – нахождение кратчайшего пути из одной вершины в любую другую.
3. Построение матрицы кратчайших расстояний – нахождение кратчайших путей для любой пары вершин.

Необходимо проложить линии коммуникаций (дороги, линии связи, электропередач и т.п.) между n заданными «точечными» объектами, при условии: во-первых, известны «расстояния» между каждой парой объектов (это может быть геометрическое расстояние или стоимость прокладки коммуникаций между ними), во-вторых, объекты могут быть связаны как непосредственно, так и с участием произвольного количества промежуточных объектов. При допущении, что разветвления возможны только в этих же n объектах, задача сводится к нахождению кратчайшего остовного дерева (SST — shortest spanning tree, или MST — minimal spanning tree) во взвешенном графе, вершины которого соответствуют заданным объектам, а веса ребер равны «расстояниям» между ними. Определение.Весостовного дерева взвешенного графа G равен сумме весов, приписанных ребрам остовного дерева. Будем обозначать (T). Минимальным остовным деревом (МОД) называется такое остовное дерево графа G, что вес T меньше или равен весу любого другого остовного дерева графа G. Вес минимального остовного дерева будем обозначать _min(T). Задача 1:найти кратчайшее остовное дерево (минимальный покрывающий остов) взвешенного графа. Пусть дан неориентированный связный граф со взвешенными ребрами. Вес ребра (x_i,x_j) обозначим c_ij. Из всех остовов графа необходимо найти один, у которого сумма весов на ребрах наименьшая. Стоимость остовного дерева вычисляется как сумма стоимостей всех рёбер, входящих в это дерево. Построение остова графа G, имеющего наименьший вес, имеет широкое применение при решении некоторого класса задач прикладного характера. Например: Пусть, например, G=(V, E, ) служит моделью железнодорожной сети, соединяющей пункты v₁, v₂, …, v_nV, а (v_i, v_j) – расстояние между пунктами v_i и v_j. Требуется проложить сеть телеграфных линий вдоль железнодорожной сети так, чтобы все пункты v₁, v₂, …, v_n были связаны между собой телеграфной сетью, протяженность которой была бы наименьшей. Рассмотрим два способа построения минимального остовного дерева взвешенного графа: алгоритм Крускала и алгоритм Прима. Алгоритм Крускала: 1) Выбрать в графе G ребро e минимального веса, не принадлежащее множеству E и такое, что его добавление в E не создает цикл в дереве T. 2) Добавить это ребро во множество ребер E. 3) Продолжить, пока имеются ребра, обладающие указанными свойствами. Пример. Для данного взвешенного графа найти минимальное корневое остовное дерево, используя алгоритм Крускала. Определить высоту построенного дерева. Алгоритм Крускала. Выбираем ребро с минимальным весом. Это ребро, (, ) с весом, равным 4. Пусть вершина будет корнем дерева. Далее выбираем ребра, инцидентные вершинам , и имеющие минимальный вес. Это ребро (, ) с весом 5. Затем к вершине присоединяем ребро (,) с весом 7. Далее, добавляем ребро (, ) с весом 7 и ребро (,) с весом 6. Минимальный вес построенного дерева равен: _min(T)=4+5+7+7+6=29.

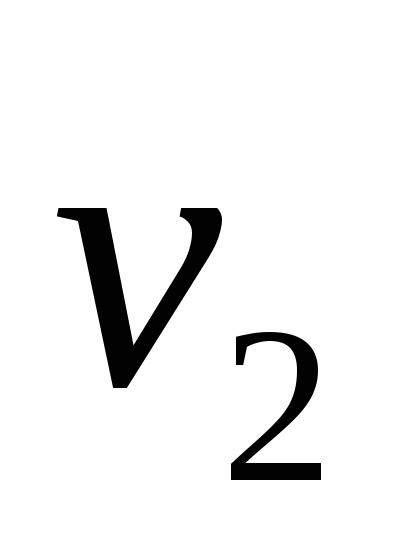
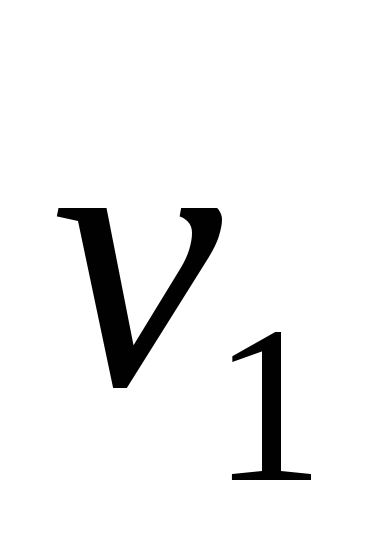
Источник

Лекция 11

Дерево. Лес (ациклический граф). Остовный подграф. Остов. Взвешенный граф. Минимальный остов. Кодирование деревьев.

Базовые понятия и утверждения

1. Определение и основные свойства деревьев.

Определение. Граф называется деревом, если он связный и в нем нет циклов.

Одноэлементный граф, т.е. граф, имеющий одну вершину и не имеющий ребер, также считается деревом.

Граф называется лесом (или ациклическим графом), если в нем нет циклов. Очевидно, что каждая компонента связности леса — дерево.

Пример 1. Граф (рис. 3.19) не является ни деревом, ни лесом. Граф (рис. 3.20) — дерево. Граф (рис. 3.21) — лес, состоящий из четырех деревьев.

Пример 2. Представьте диаграммами все (с точностью до изоморфизма) деревья с пятью вершинами.

◄ Имеется три различных (с точностью изоморфизма) дерева с пятью вершинами (рис. 3.22 — 3.24). ►

Деревья обладают рядом характеристических свойств, по наличию или отсутствию каждого их которых в рассматриваемом графе можно определить, является граф деревом или нет. Перечислим эти свойства:

1) граф — дерево в том и только в том случае, когда в нем нет циклов и ;

2) граф — дерево в том и только в том случае, когда он связный и ;

3) граф — дерево в том и только в том случае, когда он связный, и каждое его ребро является мостом;

4) граф — дерево в том и только в том случае, когда любые две вершины графа можно соединить простой цепью, притом единственной;

5) граф — дерево в том и только в том случае, когда в нем нет циклов и добавление к нему нового ребра приводит к образованию единственного простого цикла.

Также приведем одно из характеристических свойств леса: граф , имеющий компонент связности, является лесом в том и только в том случае, когда .

2. Остовы графа. Подграф графа называется остовным подграфом, если множество его вершин совпадает с множеством вершин графа .

Остовом обыкновенного графа называется его остовный подграф, являющийся деревом.

Пусть — связный граф. Если содержит хотя бы один цикл, то удалив из графа некоторое ребро этого цикла, мы уменьшим число циклов графа по крайней мере на единицу, сохранив при этом его связность. Ясно, что, последовательно разрушая циклы данного графа, можно прийти к остову графа. Поскольку дерево с вершинами имеет ровно ребро, то для получения остова нужно удалить из графа ребро, т.е. число ребер, равное цикломатическому числу связного графа .

Пусть теперь — произвольный граф с компонентами связности. Из каждой компоненты связности этого графа удалим ребро так, чтобы получился остов этой компоненты. В результате получим некоторый остовный подграф графа . Подсчитаем общее число ребер, которое нам пришлось для этого удалить. Сложив равенства , , получим:

.

Таким образом, чтобы получить остовный подграф, нужно, последовательно разрушая циклы графа, удалить из него число ребер, равное его цикломатическому числу.

Пример 3. Построим остов графа , диаграмма которого изображена на рис. 3.25. Удалим из графа ребро ; получим граф (рис. 3.26). Из графа удалим ребро ; получим граф (рис. 3.27). Из графа удалим ребро ; получим граф (рис. 3.28), который является одним из остовов графа .

Источник