Узел дерева имеющий потомков

Дерево (структура данных)

Узел является экземпляром одного из двух типов элементов графа, соответствующим объекту некоторой фиксированной природы. Узел может содержать значение, состояние или представление отдельной информационной структуры или самого дерева. Каждый узел дерева имеет ноль или более узлов-потомков, которые располагаются ниже по дереву (по соглашению, деревья ‘растут’ вниз, а не вверх, как это происходит с настоящими деревьями). Узел, имеющий потомка, называется узлом-родителем относительно своего потомка (или узлом-предшественником, или Корневые узлы [ ]

Самый верхний узел дерева называется корневым узлом. ‘Быть самым верхним узлом’ подразумевает отсутствие у корневого узла предков. Это узел, на котором начинается выполнение большинства операций над деревом (хотя некоторые алгоритмы начинают выполнение с «листов» и выполняются, пока не достигнут корня). Все прочие узлы могут быть достигнуты путём перехода от корневого узла по рёбрам (или ссылкам). (Согласно формальному определению, каждый подобный путь должен быть уникальным). В диаграммах он обычно изображается на самой вершине. В некоторых деревьях, например, Листовые узлы [ ]

Узлы самого нижнего уровня дерева называются Внутренние узлы [ ]

Внутренний узел — любой Поддеревья [ ]

Поддерево — часть деревообразной структуры данных, которая может быть представлено в виде отдельного дерева. Любой узел дерева T вместе со всеми его узлами-потомками является поддеревом дерева T. Для любого узла поддерева либо должен быть путь в корневой узел этого поддерева, либо сам узел должен являться корневым. Т.е. поддерево связано с корневым узлом целым деревом, а отношения поддерева со всеми прочими узлами определяются через понятие соответствующее поддерево (по аналогии с термином «соответствующее Упорядочивание деревьев [ ]

Существует два основных типа деревьев. В Двоичное дерево поиска — одно из разновидностей упорядоченного дерева.

Представление деревьев [ ]

Существует множество различных способов представления деревьев. Наиболее общий способ представления изображает узлы как записи, расположенные в динамически выделяемой памяти с указателями на своих потомков, предков (или и тех и других), или как элементы Деревья как графы [ ]

• Перебор всех элементов дерева
• Перебор ветви дерева
• Поиск элемента
• Вставка нового элемента в определённую позицию
• Удаление элемента
• Удаление ветви дерева (называется Общее применение [ ]

Прочие деревья [ ]

• B-дерево ( B+ дерево , R-дерево
• Список с пропусками
• T-дерево
• T-пирамида
• Ссылки [ ]

• ISBN 0-201-89683-4 . Section 2.3: Trees, pp.308–423.
• Томас Кормен , Клиффорд Штайн . Introduction to Algorithms , Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7 . Section 10.4: Representing rooted trees, pp.214–217. Chapters 12–14 (Binary Search Trees, Red-Black Trees, Augmenting Data Structures), pp.253–320.

Дополнительные источники [ ]

Источник

Терминология и определения¶

После того, как мы рассмотрели примеры деревьев, дадим формальные определения им и их компонентам.

Узел Узел — это основная часть дерева. Он может иметь название, которое мы будем называть “ключом”. Также узел может содержать дополнительную информацию, которую мы будем называть “полезной нагрузкой”. Хотя во многих алгоритмах для деревьев ей не уделяется достаточно внимания, для приложений, использующих эту структуру данных, она часто оказывается критичным фактором. Ветвь Ветвь — другая фундаментальная часть дерева. Оно соединяет два узла вместе, показывая наличие между ними определённых отношений. Каждый узел (кроме корня) имеет ровно одну входящую ветвь. При этом он может иметь несколько исходящих ветвей. Корень Корень дерева — единственный узел, не имеющий входящих ветвей. На рисунке 2 / — корень дерева. Путь Путь — это упорядоченный список узлов, соединённых ветвями. Например, Mammal \(\rightarrow\) Carnivora \(\rightarrow\) Felidae \(\rightarrow\) Felis \(\rightarrow\) Domestica — это путь. Дети (потомки) Набор узлов \(c\) , имеющих входящие ветви от одного узла, называются его детьми. На рисунке 2 узлы log/, spool/ и yp/ — потомки узла var/. Родитель (предок) Узел является родителем всех узлов, с которыми связан исходящими ветвями. На рисунке 2 узел var/ является родителем узлов log/, spool/ и yp/. Братья Узлы дерева, являющиеся детьми одного родителя, называют братьями. Примером могут послужить etc/ и usr/ в дереве файловой системы. Поддерево Поддерево — это набор узлов и ветвей, состоящий родителя и всех его потомков. Лист Лист — это узел, у которого нет детей. Например, Human и Chimpanzee — листья на рисунке 1. Уровень Уровень узла \(n\) — это число ветвей в пути от корня до \(n\) . Например, уровень Felis на рисунке 1 равен пяти. По определению, уровень корня — нулевой. Высота Высота дерева равна максимальному уровню любого его узла. Например, высота дерева на рисунке 2 равна двум.

А теперь, определившись с основной терминологией, дадим дереву формальное определение. Фактически, мы дадим две формулировки: первая будет включать узлы и ветви, а вторая (чью полезность мы докажем на практике) будет рекурсивной.

Определение 1: Дерево состоит из набора узлов и набора ветвей, соединяющих пары узлов. Оно имеет следующие свойства:

• Один из узлов дерева определён, как его корень.
• Каждый узел \(n\) (кроме корневого) соединяется ветвью с единственным другим узлом \(p\) , где \(p\) — родитель \(n\) .
• Каждый узел соединён с корнем единственно возможным путём.
• Если каждый из узлов дерева имеет максимум двух потомков, то такая структура называется двоичным деревом.

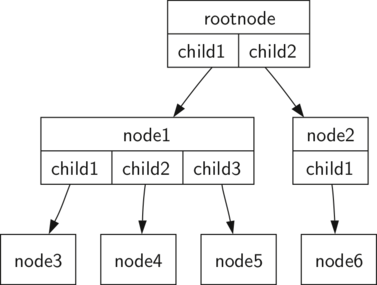
На рисунке 3 изображено дерево, удовлетворяющее определению 1. Стрелки на ветвях показывают направление связи.

Рисунок 3: Дерево, содержащее набор узлов и ветвей.

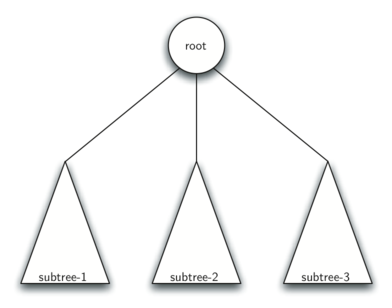
Определение 2: Дерево либо пусто, либо содержит корень и нуль или более поддеревьев, каждое из которых тоже является деревом. Корень каждого поддерева соединён ветвью с родительским деревом.

Рисунок 4 иллюстрирует это определение. Используя его, можно сказать, что изображённая структура имеет как минимум четыре узла, поскольку каждый из треугольников, представляющих поддеревья, должен иметь корень. В этом дереве может быть намного больше узлов, но сказать точнее нельзя до тех пор, пока мы не продвинемся по нему глубже.

Рисунок 4: Рекурсивное определение дерева

© Copyright 2014 Brad Miller, David Ranum. Created using Sphinx 1.2.3.

Источник

Дерево (структура данных)

Узел является экземпляром одного из двух типов элементов графа, соответствующим объекту некоторой фиксированной природы. Узел может содержать значение, состояние или представление отдельной информационной структуры или самого дерева. Каждый узел дерева имеет ноль или более узлов-потомков, которые располагаются ниже по дереву (по соглашению, деревья ‘растут’ вниз, а не вверх, как это происходит с настоящими деревьями). Узел, имеющий потомка, называется узлом-родителем относительно своего потомка (или узлом-предшественником, или Корневые узлы [ ]

Самый верхний узел дерева называется корневым узлом. ‘Быть самым верхним узлом’ подразумевает отсутствие у корневого узла предков. Это узел, на котором начинается выполнение большинства операций над деревом (хотя некоторые алгоритмы начинают выполнение с «листов» и выполняются, пока не достигнут корня). Все прочие узлы могут быть достигнуты путём перехода от корневого узла по рёбрам (или ссылкам). (Согласно формальному определению, каждый подобный путь должен быть уникальным). В диаграммах он обычно изображается на самой вершине. В некоторых деревьях, например, Листовые узлы [ ]

Узлы самого нижнего уровня дерева называются Внутренние узлы [ ]

Внутренний узел — любой Поддеревья [ ]

Поддерево — часть деревообразной структуры данных, которая может быть представлено в виде отдельного дерева. Любой узел дерева T вместе со всеми его узлами-потомками является поддеревом дерева T. Для любого узла поддерева либо должен быть путь в корневой узел этого поддерева, либо сам узел должен являться корневым. Т.е. поддерево связано с корневым узлом целым деревом, а отношения поддерева со всеми прочими узлами определяются через понятие соответствующее поддерево (по аналогии с термином «соответствующее Упорядочивание деревьев [ ]

Существует два основных типа деревьев. В натуральные числа) называется деревом с именованными рёбрами или упорядоченным деревом со структурой данных, заданной перед именованием и называемой структурой данных упорядоченного дерева.

Упорядоченные деревья являются наиболее распространёнными среди древовидных структур. Двоичное дерево поиска — одно из разновидностей упорядоченного дерева.

Представление деревьев [ ]

Существует множество различных способов представления деревьев. Наиболее общий способ представления изображает узлы как записи, расположенные в динамически выделяемой памяти с указателями на своих потомков, предков (или и тех и других), или как элементы Деревья как графы [ ]

• Перебор всех элементов дерева
• Перебор ветви дерева
• Поиск элемента
• Вставка нового элемента в определённую позицию
• Удаление элемента
• Удаление ветви дерева (называется Общее применение [ ]

Прочие деревья [ ]

• B-дерево ( B+ дерево , R-дерево
• Список с пропусками
• T-дерево
• T-пирамида
• Ссылки [ ]

• ISBN 0-201-89683-4 . Section 2.3: Trees, pp.308–423.
• Томас Кормен , Клиффорд Штайн . Introduction to Algorithms , Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7 . Section 10.4: Representing rooted trees, pp.214–217. Chapters 12–14 (Binary Search Trees, Red-Black Trees, Augmenting Data Structures), pp.253–320.

Дополнительные источники [ ]

Эта страница использует содержимое раздела Википедии на русском языке. Оригинальная статья находится по адресу: Дерево (структура данных). Список первоначальных авторов статьи можно посмотреть в истории правок. Эта статья так же, как и статья, размещённая в Википедии, доступна на условиях CC-BY-SA .

Источник