Узел дерева у которого нет предков

Задание 4. Деревья, «полиз», Хеширование

Цель работы: познакомиться с алгоритмами работы с нелинейными структурами данных, а также с современными схемами хеширования.

Краткие теоретические сведения

1. Деревья (нелинейные структуры данных)

Дерево состоит из элементов, называемых узлами. Каждый узел имеет оригинальный ключ (как правило, это целое число), данные и поля ссылки. Т.е. каждый узел может ссылаться на другие узлы и если XY узел X называется предком (родителем), а Y — потомком (сыном) или дочерним узлом. Одинаковые ключи здесь не допускаются.

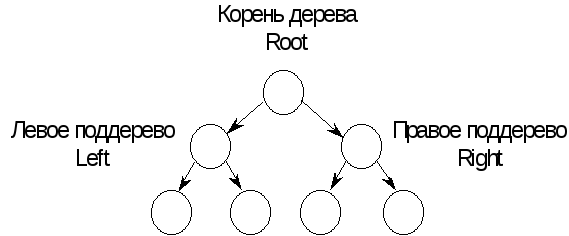
Дерево имеет единственный узел, у которого нет предков. Такой узел называют корнем дерева. Любой другой узел имеет ровно одного предка. Узел, не имеющий потомков, называется листом.

Внутренний узел – это узел, не являющийся ни листом ни корнем.

Бинарное дерево — это дерево, состоящее из узлов, ка­ждый из которых содержит не более двух ссылок на различные бинарные поддеревья, т.е. у каждого его узла (предка) может быть не более двух потомков — левый и правый. Таким образом, на каждый узел бинарного дерева имеется ровно одна ссылка.

На рисунке приведен пример бинарного дерева (корень обычно изображается сверху, хотя изображение можно и перевернуть).

Если дерево организовано так, что для каждого узла все ключи его ле­вого поддерева меньше ключа этого узла, а все ключи его правого поддерева — больше, оно называется деревом поиска.

Обычно бинарное дерево строитсясразу упорядоченным, т.е. ключ узла левого сына имеет значение меньшее, чем значение ключа у родителя, а узел правого сына — большее.

Например, если приходят числа 17, 18, 6, 5, 9, 23, 12, 7, 8, то построенное по ним дерево будет выглядеть следующим образом (для упрощения приводим только ключи):

Существуют три алгоритма обхода деревьев, которые естественно следуют из самой структуры дерева.

1. Обход слева направо: Left-Root-Right: сначала посещаем левое поддерево, затем — корень и, наконец, правое поддерево.

2. Построение обратной польской записи

Одной из главных причин, лежащих в основе появления языков программирования высокого уровня, явились вычислительные задачи, требующие больших объемов вычислений. Поэтому к языкам программирования предъявлялись требования максимального приближения формы записи арифметических выражений к естественному языку математики с последующим их вычислением путем их трансляции. Здесь наибольшее распространение получил метод трансляции с помощью обратной польской записи («ПОЛИЗ»), которую предложил польский математик Я.Лукашевич: – представление перед вычислениями арифметического выражения в постфиксной форме. И прежде чем рассмотреть конкретные примеры, познакомимся с различными способами записи арифметических выражений. Пусть для операндов a и b выполняется операция сложения. Мы привыкли записывать это в виде a+b. Такая форма записи называется инфиксной.Наряду с этой формой записи существуют еще префиксная(+ab) и постфиксная(ab+) формы записи арифметических выражений. Отличаются они друг от друга положением знака операции по отношению к операндам: — в инфиксной записи знак операции располагается между операндами, над которыми эта операция выполняется; — в префиксной записи знак операции предшествует соответствующим операндам, а в постфиксной — знак операции располагается за операндами. Пример. Использование бинарного дерева. Пусть задано простое арифметическое выражение вида: (a+b)*(c+d)-e(5.1) Представим это выражение в виде дерева, в котором узлам соответствуют операции, а листьям — операнды. Алгоритм построения такого дерева следующий.

1. Построение начинают с корня, в качестве которого выбирается операция, выполняющаяся последней. Левой ветви соответствует левый операнд операции, а правой ветви — правый.
2. Если выражение сложное, то далее в узлах очередного уровня размещают операции по восходящей очередности их выполнения.
3. В узлы последнего уровня помещают операции, которые будут выполнены в первую очередь.
4. И наконец операнды – листья дерева.

Дерево выражения (5.1) имеет вид: 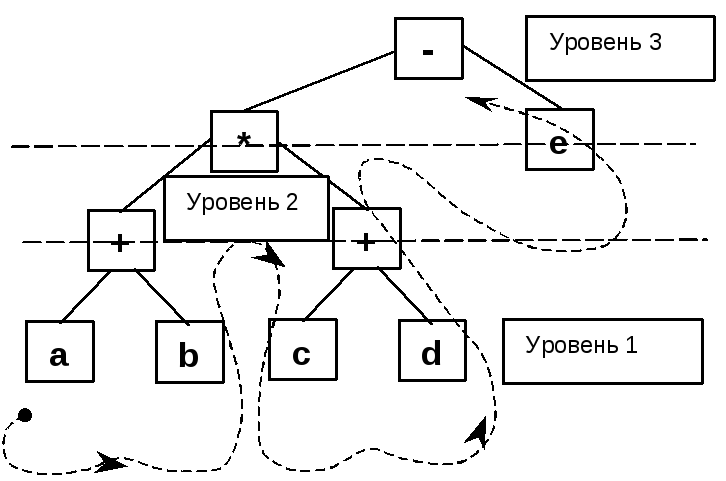Совершим обход дерева, под которым будем понимать формирование строки символов из символов узлов и ветвей дерева. Обход будем совершать от самой левой ветви вправо и узел переписывать в выходную строку только после рассмотрения всех его ветвей (обход по алгоритму «Левое поддерево – Правое поддерево – Корень», строго по уровням, т.е. последовательно снизу вверх). Результат обхода дерева имеет вид: ab+cd+*e— (5.2) Характерные особенности выражения (2) состоят в следовании символов операций за символами операндов и в отсутствии скобок. Такая запись называется обратной польской записью. Обратная польская запись — идеальный промежуточный язык при трансляции: вычисление выражения, записанного в обратной польской записи, проводится путем его однократного просмотра слева направо, что является весьма удобным при генерации объектного кода программ. Алгоритм вычислений «ПОЛИЗ» следующий:

1. Если текущий элемент записи – операнд. То переходим к следующему элементу.
2. Если же текущий элемент записи – символ операции, то эта операция выполняется над ближайшими двумя операндами, расположенными слева от этой операции. Полученный результат размещают на месте самого левого операнда а сами операнды и символ операции из «ПОЛИЗа» вычеркивают.

В результате последовательно будут выполнены все операции а сама запись сократится до одного элемента: конечного результата. Например, вычисление выражения (2) может быть проведено следующим образом:

№	Анализируемая строка	Действие
1	аb+сd+*e-	r1=a+b
2	r1cd+*e-	r2=c+d
3	r1r2*e-	r1=r1*r2
4	r1e-	r1=r1-e
5	r1

Здесь r1и r2 — вспомогательные переменные. r1 на пятом уровне – конечный результат

Источник

Как называется узел дерево который не имеет предков?

У нас есть 15 ответов на вопрос Как называется узел дерево который не имеет предков? Скорее всего, этого будет достаточно, чтобы вы получили ответ на ваш вопрос.

Как называется узел дерева, который не имеет предков? Ответ: 3. Отметьте все элементы, которые могут присутствовать в дереве.

Как называется дерево в котором каждый узел может иметь?

Лист — узел, не имеющий дочерних элементов (потомков). Внутренний узел — узел дерева, имеющий потомков. Глубина дерева — самый длинный путь от корня дерева до его листа. Дерево, в котором каждый узел имеет не более двух потомков, называется двоичным деревом.

Как называется узел дерево который не имеет предков? Ответы пользователей

Как называется узел дерева, который не имеет предков? Ответ: 3. Отметьте все элементы, которые могут присутствовать в дереве.

Узел, не имеющий предков (самый верхний), называется корневым узлом. Это узел, на котором начинается выполнение большинства операций над .

Узел, не имеющий потомков, называется – ЛИСТ. автор вопроса выбрал этот ответ лучшим. комментировать. в избранное ссылка .

корневой узел — самый верхний узел дерева, он не имеет предков (на рисунке узел «Книга»); . Этих детей называют левым (Л) и правым (П) потомком или «сыном».

Корневой узел не имеет предков, а листья не имеют потомков. Также у дерева есть высота (глубина). Она определяется числом уровней, на которых .

Корнем этого дерева является узел Книга, который имеет три поддерева соответь . Предок или потомок узла, не являющийся таковым самого себя, называется ис+.

Корень не имеет предков; . Бинарное дерево — это конечное множество узлов, которое или пусто, . Узел с ключом X имеет не более одного потомка.

Элемент дерева, который не ссылается на другие, называется корнем, листом, . каждый узел имеет не менее двух предков, от корня до листа не более двух .

Источник

Как называется узел дерева у которых нет потомков?

У нас есть 20 ответов на вопрос Как называется узел дерева у которых нет потомков? Скорее всего, этого будет достаточно, чтобы вы получили ответ на ваш вопрос.

Лист — узел, не имеющий дочерних элементов (потомков). Внутренний узел — узел дерева, имеющий потомков.

Как называется узел не имеющий потомков?

Узел, не имеющий предков (самый верхний), называется корневым узлом.

Сколько потомков имеет узел А?

6. Сколько потомков имеет узел А? Ответ: 7.

Как называется часть дерева которое тоже является деревом?

Определение 2: Дерево либо пусто, либо содержит корень и нуль или более поддеревьев, каждое из которых тоже является деревом. Корень каждого поддерева соединён ветвью с родительским деревом.

Какие узлы являются предками узла Д?

Каждый узел, кроме корневого, связан только с одним узлом более высокого уровня, называемым узлом-предком. Например, для узла D предком является узел A, предок для узла G — это D и т.

Что такое внутренний узел дерева?

Внутренний узел — узел дерева, имеющий потомков. Глубина дерева — самый длинный путь от корня дерева до его листа. Дерево, в котором каждый узел имеет не более двух потомков, называется двоичным деревом.

Как называется дерево каждый узел которого имеет не более двух сыновей ответ?

Дерево, в котором каждый узел имеет не более двух потомков, называется двоичным деревом.

Как называются узлы что находятся на одном уровне в авл дереве?

Иерархическая структура элементов, называемыми узлами (вершинами). На самом верхнем уровне имеется только один узел — корень дерева.

Источник

Терминология и определения¶

После того, как мы рассмотрели примеры деревьев, дадим формальные определения им и их компонентам.

Узел Узел — это основная часть дерева. Он может иметь название, которое мы будем называть “ключом”. Также узел может содержать дополнительную информацию, которую мы будем называть “полезной нагрузкой”. Хотя во многих алгоритмах для деревьев ей не уделяется достаточно внимания, для приложений, использующих эту структуру данных, она часто оказывается критичным фактором. Ветвь Ветвь — другая фундаментальная часть дерева. Оно соединяет два узла вместе, показывая наличие между ними определённых отношений. Каждый узел (кроме корня) имеет ровно одну входящую ветвь. При этом он может иметь несколько исходящих ветвей. Корень Корень дерева — единственный узел, не имеющий входящих ветвей. На рисунке 2 / — корень дерева. Путь Путь — это упорядоченный список узлов, соединённых ветвями. Например, Mammal \(\rightarrow\) Carnivora \(\rightarrow\) Felidae \(\rightarrow\) Felis \(\rightarrow\) Domestica — это путь. Дети (потомки) Набор узлов \(c\) , имеющих входящие ветви от одного узла, называются его детьми. На рисунке 2 узлы log/, spool/ и yp/ — потомки узла var/. Родитель (предок) Узел является родителем всех узлов, с которыми связан исходящими ветвями. На рисунке 2 узел var/ является родителем узлов log/, spool/ и yp/. Братья Узлы дерева, являющиеся детьми одного родителя, называют братьями. Примером могут послужить etc/ и usr/ в дереве файловой системы. Поддерево Поддерево — это набор узлов и ветвей, состоящий родителя и всех его потомков. Лист Лист — это узел, у которого нет детей. Например, Human и Chimpanzee — листья на рисунке 1. Уровень Уровень узла \(n\) — это число ветвей в пути от корня до \(n\) . Например, уровень Felis на рисунке 1 равен пяти. По определению, уровень корня — нулевой. Высота Высота дерева равна максимальному уровню любого его узла. Например, высота дерева на рисунке 2 равна двум.

А теперь, определившись с основной терминологией, дадим дереву формальное определение. Фактически, мы дадим две формулировки: первая будет включать узлы и ветви, а вторая (чью полезность мы докажем на практике) будет рекурсивной.

Определение 1: Дерево состоит из набора узлов и набора ветвей, соединяющих пары узлов. Оно имеет следующие свойства:

• Один из узлов дерева определён, как его корень.
• Каждый узел \(n\) (кроме корневого) соединяется ветвью с единственным другим узлом \(p\) , где \(p\) — родитель \(n\) .
• Каждый узел соединён с корнем единственно возможным путём.
• Если каждый из узлов дерева имеет максимум двух потомков, то такая структура называется двоичным деревом.

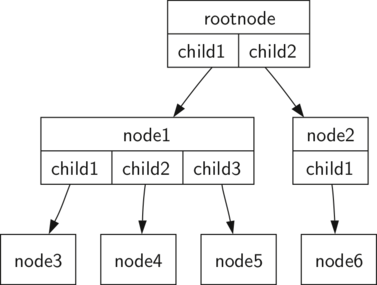
На рисунке 3 изображено дерево, удовлетворяющее определению 1. Стрелки на ветвях показывают направление связи.

Рисунок 3: Дерево, содержащее набор узлов и ветвей.

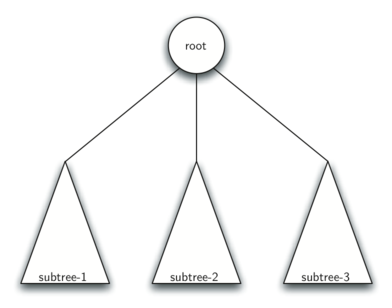
Определение 2: Дерево либо пусто, либо содержит корень и нуль или более поддеревьев, каждое из которых тоже является деревом. Корень каждого поддерева соединён ветвью с родительским деревом.

Рисунок 4 иллюстрирует это определение. Используя его, можно сказать, что изображённая структура имеет как минимум четыре узла, поскольку каждый из треугольников, представляющих поддеревья, должен иметь корень. В этом дереве может быть намного больше узлов, но сказать точнее нельзя до тех пор, пока мы не продвинемся по нему глубже.

Рисунок 4: Рекурсивное определение дерева

© Copyright 2014 Brad Miller, David Ranum. Created using Sphinx 1.2.3.

Источник