Вес дерева графа равен

5.14. Остовные деревья

Остовным деревом (остовом или каркасом) связного графа G называется любой его подграф, содержащий все вершины графа G и являющийся деревом. Остовное дерево графа не единственно.

На рис. 37 изображен граф G и два его остовных дерева G₁ и G₂.

Теорема. Число ребер произвольного графа G, которые необходимо удалить для получения остова, не зависит от последовательности их удаления и равно цикломатическому числу графа

ν(G)= m – n + k,

где m – число дуг, n – число вершин, k – число компонент связности графа

Следствие 1. Граф G является лесом тогда и только тогда , когда ν(G)=0.

Следствие 2. Граф G имеет единственный цикл тогда и только тогда, когда ν(G)=1.

Следствие 3. Граф, в котором число ребер не меньше, чем число вершин, содержит цикл

Для графа рис. m=5, n=4, k =1. Следовательно, надо удалить из графа две дуги, чтобы получить остов. Остовами этого графа будут графы G₁ и G₂.

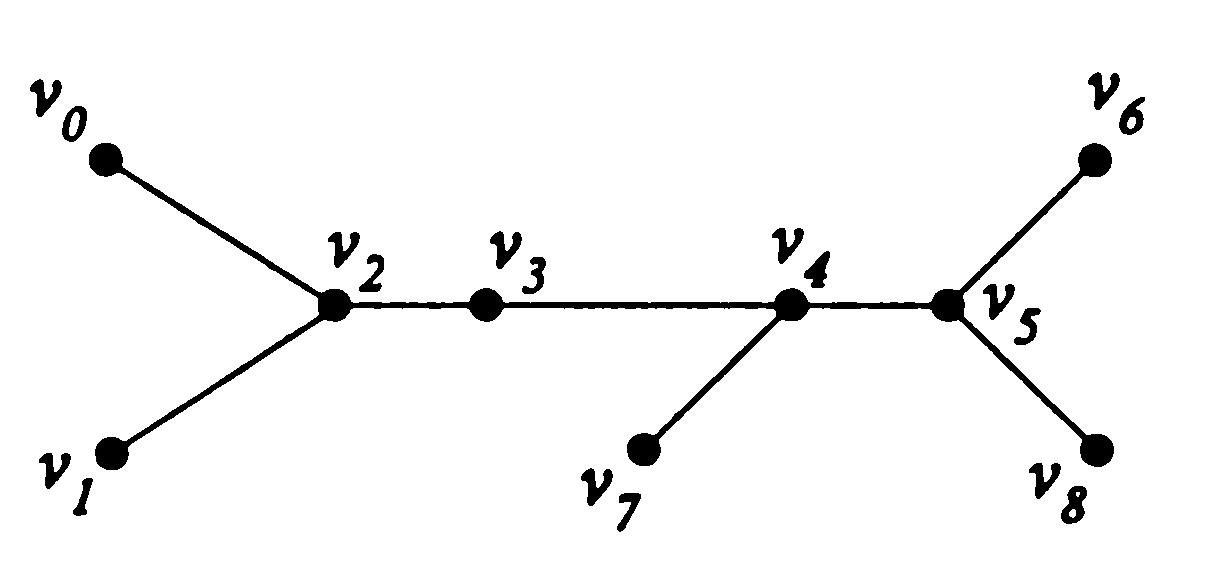
Для графа G, изображенного на рис. 38, m =8, n =7, k =2. Следовательно, надо удалить из графа три дуги, чтобы получить остов. Это можно сделать так, чтобы получился граф G₁, который представляет собой лес из двух деревьев.

Существует простой способ определить количество различных остовов мультиграфа с n вершинами. Для этого нужно записать матрицу A размера , по главной диагонали которой выписаны степени вершин, а недиагональные элементы равны взятому со знаком минус числу ребер, связывающих вершины i и j. Вычислив минор любого элемента главной диагонали матрицы A, получим искомое число возможных остовов графа. Например, для графа на рис. 39 имеем:

т.е. получаем 12 различных каркасов.

Эффективным методом построения каркаса графа является “подключение” очередного ребра к каркасу без образования циклов. Процедура основана на просмотре в произвольном порядке ребер исходного графа и может быть представлена как процесс окрашивания их. В синий цвет окрашиваются ребра, включаемые в остов, а в красный –ребра, не включаемые в остов. При рассмотрении ребра осуществляется проверка того, не образует ли данное ребро в совокупности с синими ребрами, уже включенными в остов, цикл. Поскольку синие ребра, включенные в остов в процессе присоединения, составляют граф, имеющий одну или несколько компонент связности, то следующая присоединяемое ребро либо попадает в «букет» или «букеты» одной вершиной (встраивается в одну из компонент связности, участвуя в построении каркаса), либо двумя (происходит образование цикла, а ребро бракуется).

5.15 Взвешенные графы. Экстремальные остовы графов

Если требуется построить каркас наиболее экономичным образом, например, построить автомобильные дороги, связывающие дачные поселки, так, чтобы их суммарная длина была наименьшей, то задачи подобного рода решаются с помощью взвешенных графов.

Любой простой граф называется взвешенным графом, если каждому ребру приписывается вес μ_i, выражающий численно расстояние, стоимость или иную величину, характеризующую взаимосвязь между парами вершин графа.

Для описания взвешенного графа (орграфа) используется взвешенная матрица смежности размерности . Каждый элемент задает вес («стоимость») ребра (дуги). Для простых графов взвешенная матрица смежности симметрична относительно главной диагонали.

Пример 5.8. Графу, изображенному на рис. 40, соответствует взвешенная матрица смежности

Требуется выявить такой остов этого графа, чтобы суммарный вес ветвей остова был минимальным (или максимальным). Такой остов графа называют его экстремальным деревом.

Минимальным каркасным деревом графа является каркасное дерево во взвешенном графе, имеющее минимальный общий вес ребер.

Для решения задач такого рода разработаны эффективные алгоритмы, например, алгоритмом Краскала. На первом шаге выбирается первая ветвь искомого остова, для чего выбирается ребро графа с наименьшим (наибольшим) весом. Затем на каждом следующем шаге рассматривается минимальное по весу ребро и, если оно не образует цикла с ранее выбранными ветвями, вводится в остов. Построение заканчивается после отбора для остова n-1 ребер.

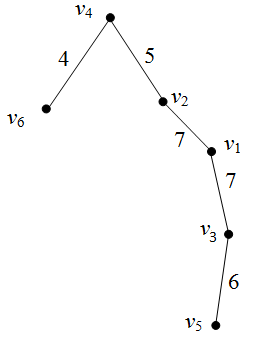
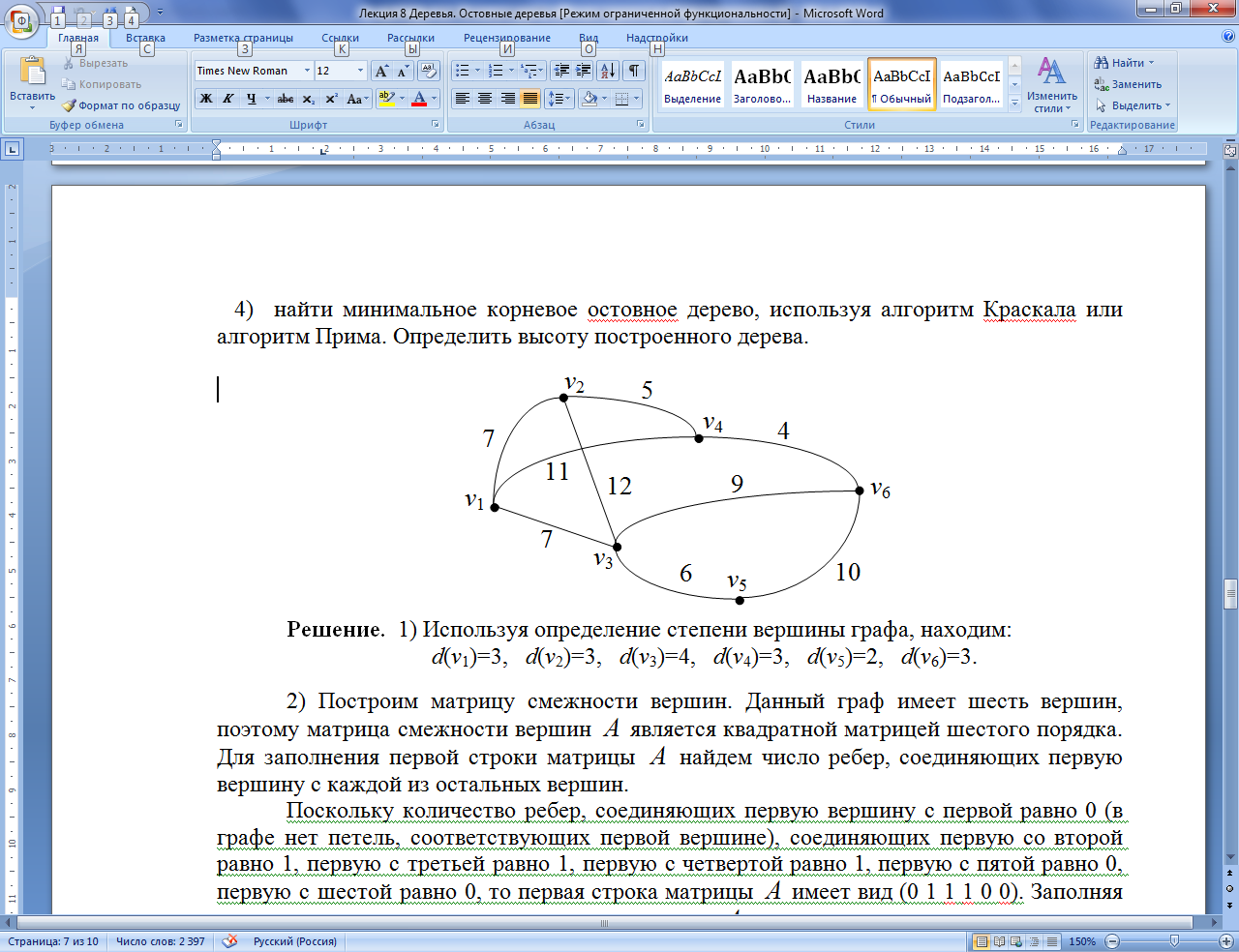
П ример 5.9 Применим алгоритм Краскала для нахождения минимального каркаса графа, изображенного на рис. 41.

Упорядоченный по возрастанию стоимости список ребер выглядит так: (a,d)₁, (e,f)₁, (h,i)₁, (a,e)₂, (b,f)₂, (d,e)₂, (e,g),₂ (a,b)₃, (f,g)₃, (f,h)₄, (c,i)₄, (f,i)₄, (g,h)₅, (c,f)₆.

Действуя по алгоритму, последовательно поместим в минимальное каркасное дерево T ребра (a,d), (e,f), (h,i), (a,e) и (b,f). На следующем шаге из списка будет взято ребро (e,g),

поскольку оно в списке после ребра (b,f) оказалось первым, не приводящим к образованию цикла. Ребра (a,b), (f,g) выбраковываются, а добавляется следующие ребра (f,h), (c,i). На этом построение минимального каркасного дерева закончено (рис. 42).

Источник

8. Остовы и деревья

Понятие дерева широко используется во многих областях математики и информатики. Например, как инструмент при вычислениях, как удобный способ хранения данных, способ сортировки или поиска данных.

Достаточно развитое генеалогическое дерево образует дерево.

Типичное частичное организационное дерево для университета.

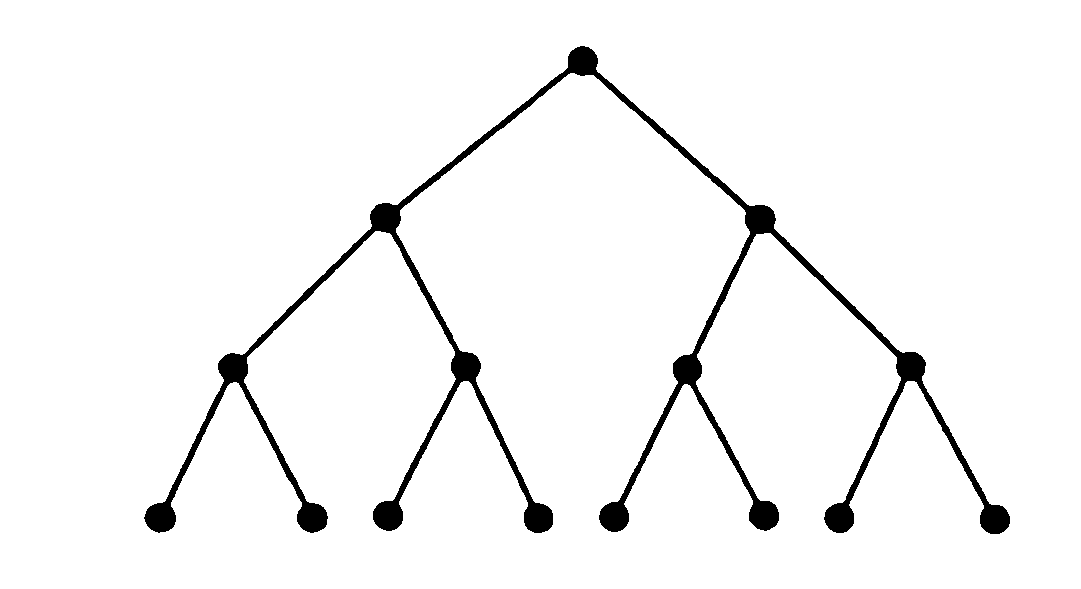
Если дерево имеет хотя бы одно ребро, оно имеет две вершины со степенью 1. Вершины со степенью 1 называются листьями. Другие вершины называются внутренними вершинами.

Предположим, что дерево представляет физический объект, подвижный в вершинах, и подвесим дерево за одну из его вершин:

Если подвесить за вершину V3 или V4

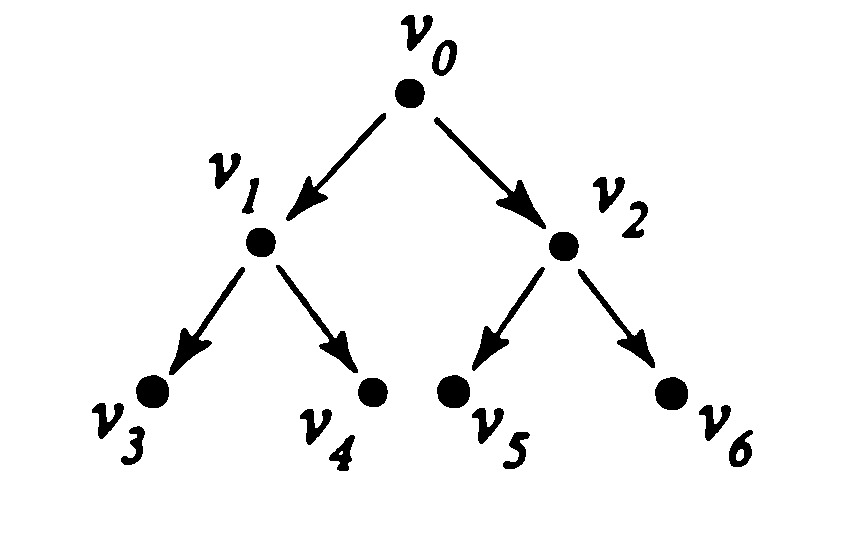
Вершина в верхней части называется корнем дерева, если корень определен, то дерево называется корневым. При необходимости корневое дерево Т можно заменить на ориентированное корневое дерево Т’, порожденное корневым деревом Т.

Если корень выбран, уровень вершины V определяется длиной единственного пути из корня в вершину V. Высотой дерева называется длина самого длинного пути от корня дерева до листа.

Если рассматривается корневое ориентированное дерево Т’, порожденное данным корневым деревом Т, тогда вершина u называется родителем вершины v; a v называется сыном вершины u, если существует ориентированное ребро из u в v.

Если u — родитель v и v1, тогда v и v1 называются братьями.

Если существует ориентированный путь из вершины u в вершину v, тогда u называется предком вершины v, a v называется потомком вершины u.

Если наибольшая из степеней выхода для вершин дерева равна m, тогда дерево называется m — арным деревом.

В частном случае, когда m = 2, дерево называется бинарным деревом.

В каждом бинарном дереве каждый сын родителя обозначается либо как левый сын, либо как правый сын (но не то и другое одновременно).

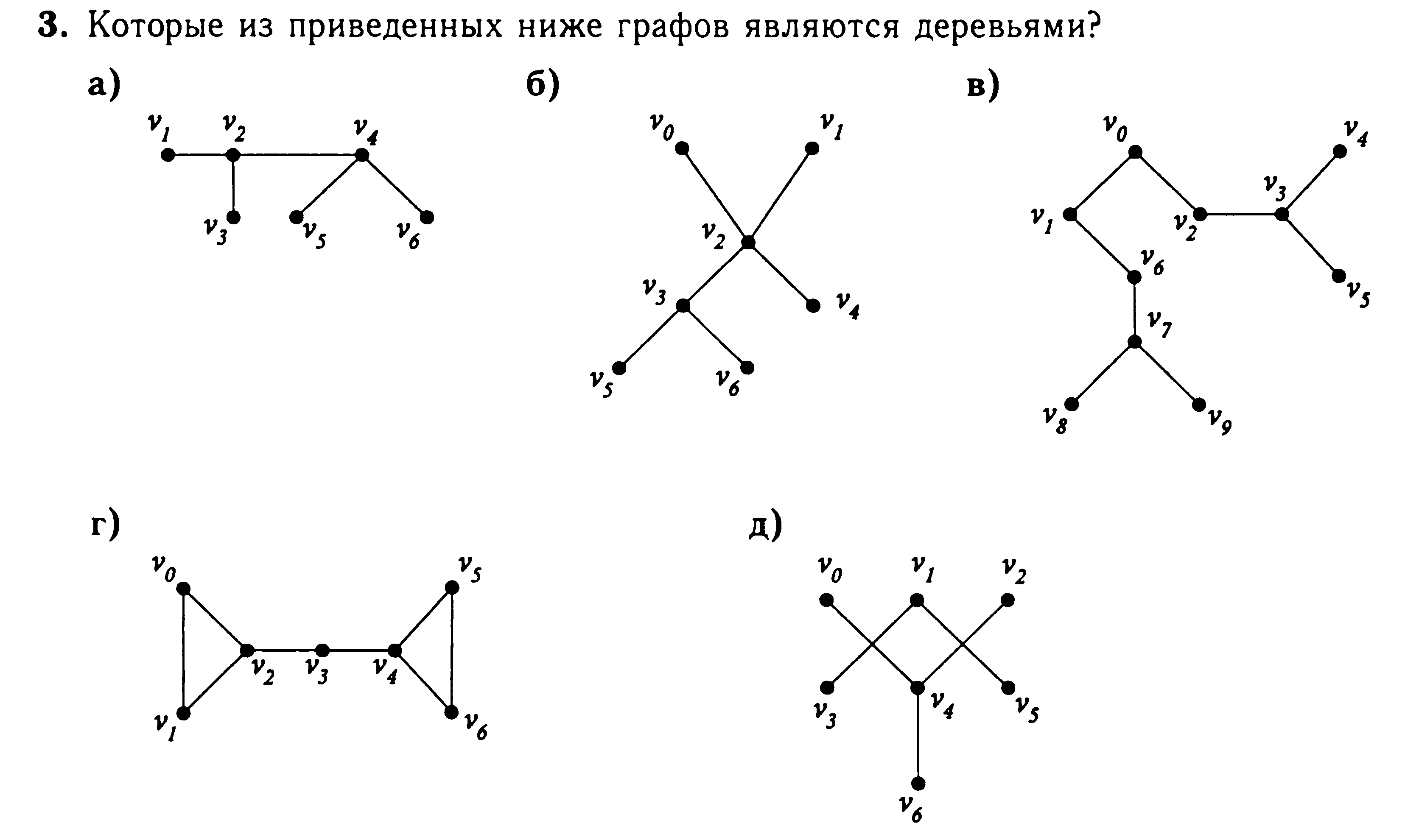
Связный граф G(V,E), не имеющий циклов, называется деревом.

ТЕОРЕМА (основные свойства деревьев):

Пусть граф G(V,E) имеет n вершин. Тогда следующие утверждения эквивалентны:

1. G является деревом;
2. G не содержит циклов и имеет n-1 рёбер;
3. G связен и имеет n-1 рёбер;
4. G связен, но удаление » ребра нарушает связность;
5. » две вершины графа G соединены ровно одним путём;
6. G не имеет циклов, но добавление » ребра порождает ровно один цикл.

Ориентированное дерево представляет собой ориентированный граф без циклов, в котором полустепень захода каждой вершины (за исключением одной, например v₁) не больше 1, а полустепень захода вершины v₁ (называемой также корнем) равна нулю. Вершину v ордерева называют потомком вершины u, если $ путь из u в v. В этом же случае вершину u называют предком вершины v. Вершину, не имеющую потомков, называют листом. 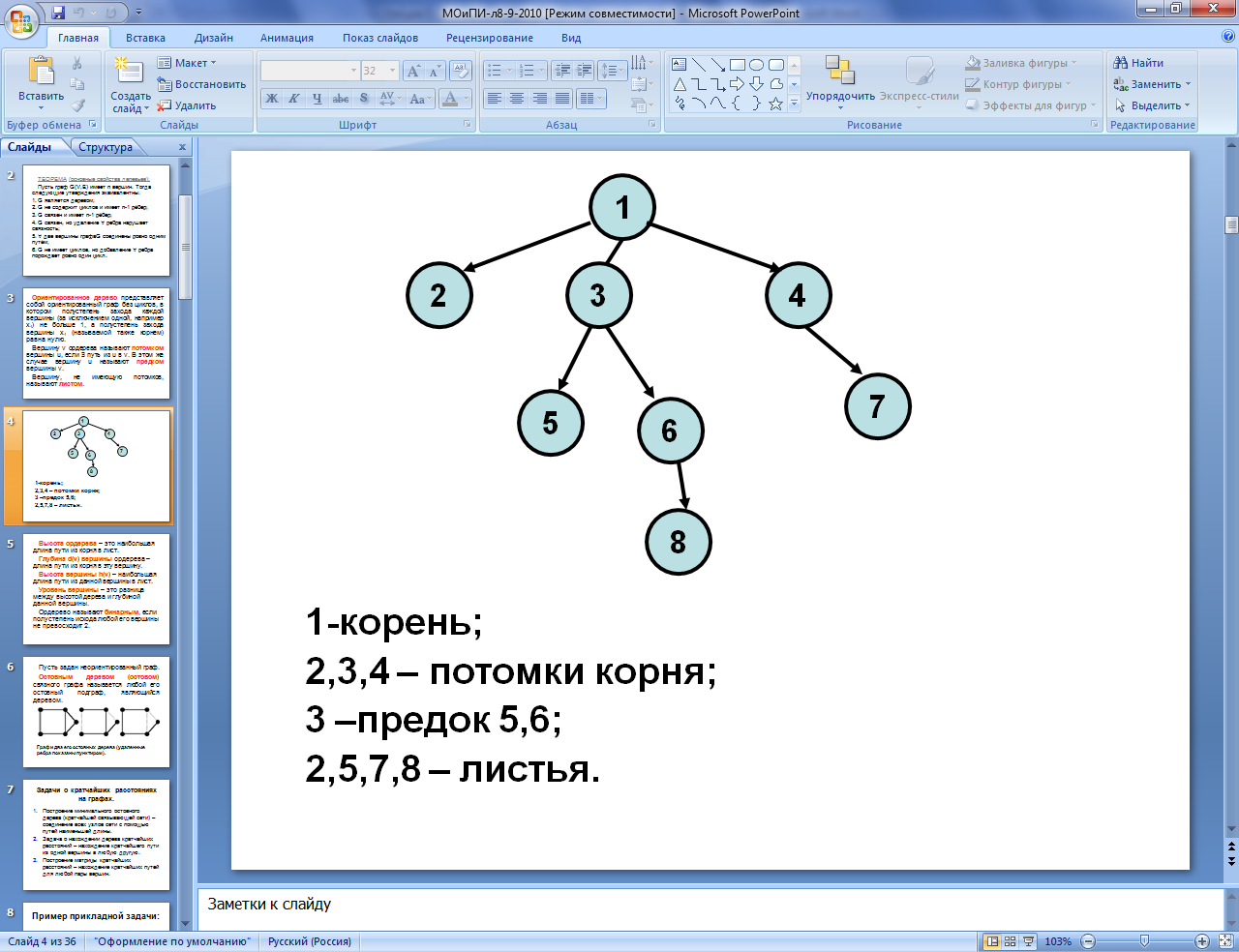Высота ордерева – это наибольшая длина пути из корня в лист. Уровень вершины ордерева – длина пути из корня в эту вершину. Ордерево называют бинарным, если полустепень исхода любой его вершины не превосходит 2. Пусть задан неориентированный граф. Остовным деревом (остовом) связного графа называется любой его остовный подграф, являющийся деревом. Граф и два его остовных дерева (удаленные ребра показаны пунктиром).Задачи о кратчайших расстояниях на графах.

1. Построение минимального остовного дерева (кратчайшей связывающей сети) – соединение всех узлов сети с помощью путей наименьшей длины.
2. Задача о нахождении дерева кратчайших расстояний – нахождение кратчайшего пути из одной вершины в любую другую.
3. Построение матрицы кратчайших расстояний – нахождение кратчайших путей для любой пары вершин.

Необходимо проложить линии коммуникаций (дороги, линии связи, электропередач и т.п.) между n заданными «точечными» объектами, при условии: во-первых, известны «расстояния» между каждой парой объектов (это может быть геометрическое расстояние или стоимость прокладки коммуникаций между ними), во-вторых, объекты могут быть связаны как непосредственно, так и с участием произвольного количества промежуточных объектов. При допущении, что разветвления возможны только в этих же n объектах, задача сводится к нахождению кратчайшего остовного дерева (SST — shortest spanning tree, или MST — minimal spanning tree) во взвешенном графе, вершины которого соответствуют заданным объектам, а веса ребер равны «расстояниям» между ними. Определение.Весостовного дерева взвешенного графа G равен сумме весов, приписанных ребрам остовного дерева. Будем обозначать (T). Минимальным остовным деревом (МОД) называется такое остовное дерево графа G, что вес T меньше или равен весу любого другого остовного дерева графа G. Вес минимального остовного дерева будем обозначать _min(T). Задача 1:найти кратчайшее остовное дерево (минимальный покрывающий остов) взвешенного графа. Пусть дан неориентированный связный граф со взвешенными ребрами. Вес ребра (x_i,x_j) обозначим c_ij. Из всех остовов графа необходимо найти один, у которого сумма весов на ребрах наименьшая. Стоимость остовного дерева вычисляется как сумма стоимостей всех рёбер, входящих в это дерево. 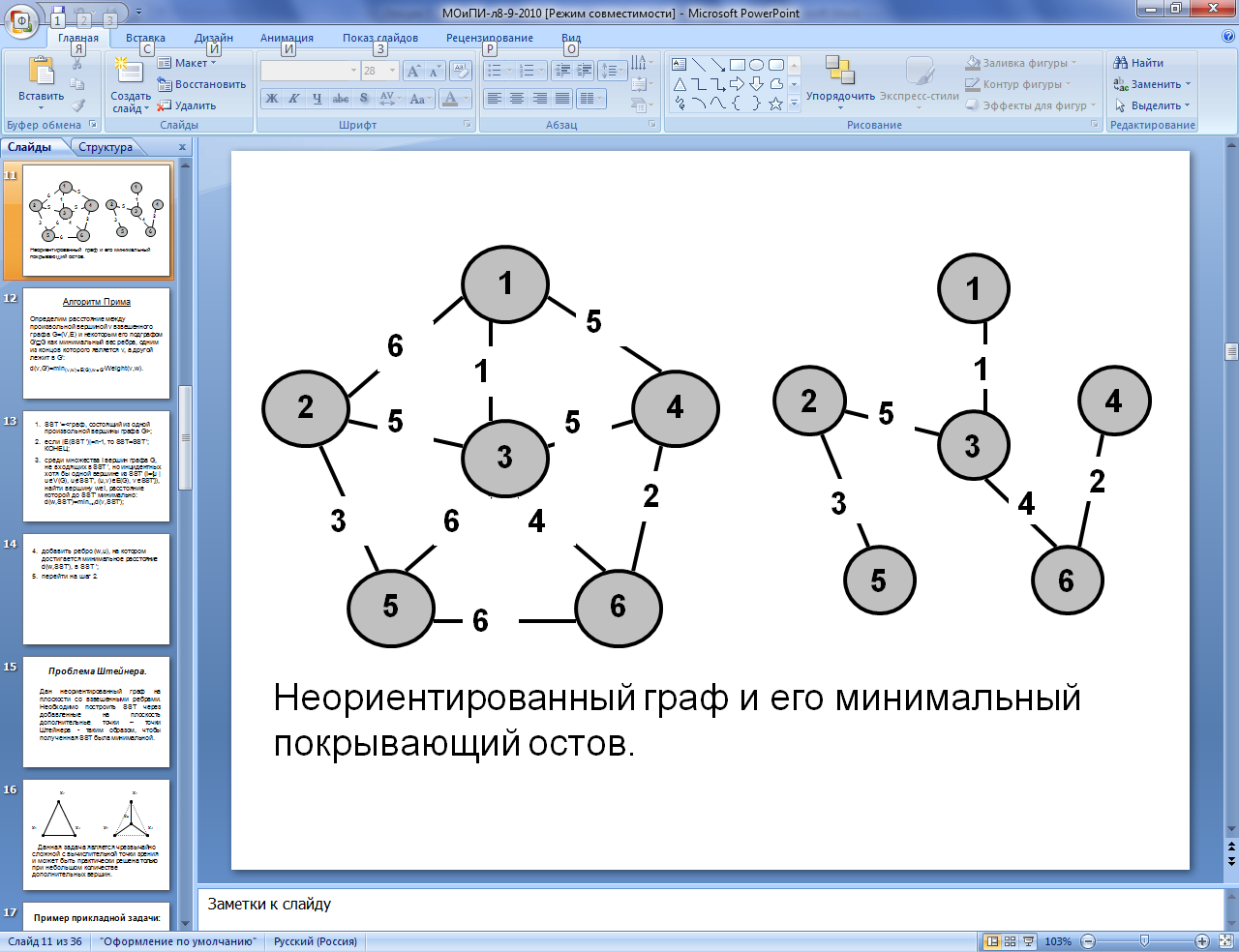Построение остова графа G, имеющего наименьший вес, имеет широкое применение при решении некоторого класса задач прикладного характера. Например: Пусть, например, G=(V, E, ) служит моделью железнодорожной сети, соединяющей пункты v₁, v₂, …, v_nV, а (v_i, v_j) – расстояние между пунктами v_i и v_j. Требуется проложить сеть телеграфных линий вдоль железнодорожной сети так, чтобы все пункты v₁, v₂, …, v_n были связаны между собой телеграфной сетью, протяженность которой была бы наименьшей. Рассмотрим два способа построения минимального остовного дерева взвешенного графа: алгоритм Крускала и алгоритм Прима. Алгоритм Крускала: 1) Выбрать в графе G ребро e минимального веса, не принадлежащее множеству E и такое, что его добавление в E не создает цикл в дереве T. 2) Добавить это ребро во множество ребер E. 3) Продолжить, пока имеются ребра, обладающие указанными свойствами. Пример. Для данного взвешенного графа найти минимальное корневое остовное дерево, используя алгоритм Крускала. Определить высоту построенного дерева. Алгоритм Крускала. Выбираем ребро с минимальным весом. Это ребро, (, ) с весом, равным 4. Пусть вершина будет корнем дерева. Далее выбираем ребра, инцидентные вершинам , и имеющие минимальный вес. Это ребро (, ) с весом 5. Затем к вершине присоединяем ребро (,) с весом 7. Далее, добавляем ребро (, ) с весом 7 и ребро (,) с весом 6. Минимальный вес построенного дерева равен: _min(T)=4+5+7+7+6=29.

Источник