Визуализация красно черного дерева

Saved searches

Use saved searches to filter your results more quickly

You signed in with another tab or window. Reload to refresh your session. You signed out in another tab or window. Reload to refresh your session. You switched accounts on another tab or window. Reload to refresh your session.

Red–Black Tree Visualization using React JS

nadakamel/RedBlackTree-Visualization

This commit does not belong to any branch on this repository, and may belong to a fork outside of the repository.

Name already in use

A tag already exists with the provided branch name. Many Git commands accept both tag and branch names, so creating this branch may cause unexpected behavior. Are you sure you want to create this branch?

Sign In Required

Please sign in to use Codespaces.

Launching GitHub Desktop

If nothing happens, download GitHub Desktop and try again.

Launching GitHub Desktop

If nothing happens, download GitHub Desktop and try again.

Launching Xcode

If nothing happens, download Xcode and try again.

Launching Visual Studio Code

Your codespace will open once ready.

There was a problem preparing your codespace, please try again.

Latest commit

Git stats

Files

Failed to load latest commit information.

README.md

Red–Black Tree Visualization

1. Download Node.js from the below link if you don’t have it on your machine. https://nodejs.org/en/download/
2. Clone this repository to your machine using your machine’s Terminal. git clone https://github.com/nadakamel/RedBlackTree-Visualization.git
3. Using Terminal, cd into project’s folder directory cd ~/RedBlackTree-Visualization
4. Download node_modules folder to the project using this command line npm install
5. Run the project on Terminal using this command line npm start

A red–black tree is a kind of self-balancing binary search tree in computer science. Each node of the binary tree has an extra bit, and that bit is often interpreted as the color (red or black) of the node. These color bits are used to ensure the tree remains approximately balanced during insertions and deletions.

Balance is preserved by painting each node of the tree with one of two colors in a way that satisfies certain properties, which collectively constrain how unbalanced the tree can become in the worst case. When the tree is modified, the new tree is subsequently rearranged and repainted to restore the coloring properties. The properties are designed in such a way that this rearranging and recoloring can be performed efficiently.

The balancing of the tree is not perfect, but it is good enough to allow it to guarantee searching in O(log n) time, where n is the total number of elements in the tree. The insertion and deletion operations, along with the tree rearrangement and recoloring, are also performed in O(log n) time.

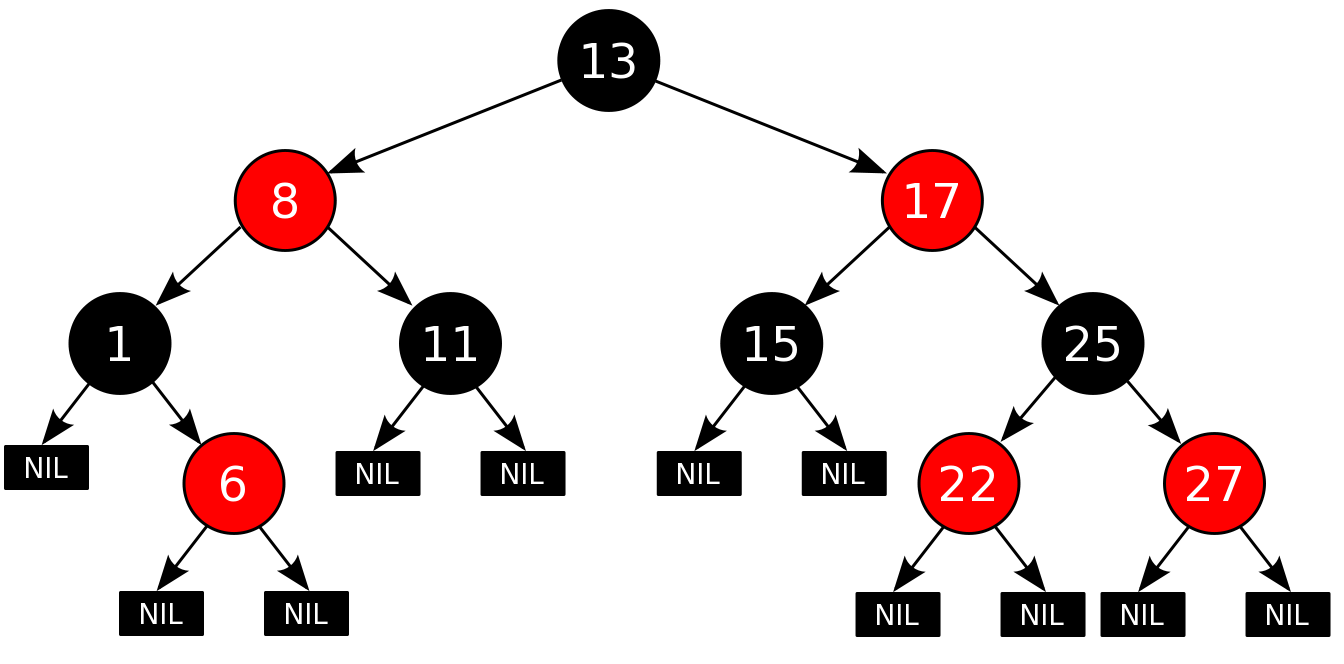
An example of a red–black tree:

In addition to the requirements imposed on a binary search tree the following must be satisfied by a red–black tree:

• Each node is either red or black.
• The root is black. This rule is sometimes omitted. Since the root can always be changed from red to black, but not necessarily vice versa, this rule has little effect on analysis.
• All leaves (NIL) are black.
• If a node is red, then both its children are black.
• Every path from a given node to any of its descendant NIL nodes contains the same number of black nodes.

Some definitions: the number of black nodes from the root to a node is the node’s black depth; the uniform number of black nodes in all paths from root to the leaves is called the black-height of the red–black tree.

These constraints enforce a critical property of red–black trees: the path from the root to the farthest leaf is no more than twice as long as the path from the root to the nearest leaf. The result is that the tree is roughly height-balanced. Since operations such as inserting, deleting, and finding values require worst-case time proportional to the height of the tree, this theoretical upper bound on the height allows red–black trees to be efficient in the worst case, unlike ordinary binary search trees.

Источник

Красно-чёрные деревья на javascript

Привет Хабр! Изучал недавно красно-черные деревья. Попробовал визуализировать детали работы алгоритмов вставки и удаления на d3.js. Надеюсь, полученный результат поможет сэкономить немного времени тем, кто изучает алгоритмы на javascript. Посмотреть можно тут. Исходник реализации, от которой отталкивался тут . Под катом краткие подробности.

Поиск существующих решений

Главной целью задумки было разобраться в реализации алгоритма и визуализировать ее. Первым делом стал искать реализацию с полными и понятными пояснениями и кодом на js. В процессе поиска опечалило, что авторы временами недоделывают исходник, например, тут есть алгоритм вставки, но нету удаления. Или делают визуализацию как тут , но не дают ссылки на исходник. Потом нашел вот эту отличную статью. Но хоть убейте, до сих пор не могу понять почему автор вставил код картинками и не дал по запросу в коментах ссылку на исходник. Есть еще npm пакет red-black-tree , весь исходный код которого: ‘in progress. ‘ в readme. Также нашлась популярная реализация красно-черных деревьев на js, от которой зависит куча пакетов и миллионы закачек в неделю, но код там устарел лет на пять.

Расстановка приоритетов и конкретизация задачи

Пораскинув мозгами, решил, что читаемость и понятность кода для учебных целей приоритетнее, поэтому взял за основу статью, которую упоминал вначале, а не npm пакет. Реализация оказалась более удобной и наглядной в плане чтения кода. В статье автор начинает с двоичного дерева, потом расширяет его до красно-черного. Для визуализации выглядит вполне логичным наследовать от красно-черного дерева и сделать анимированное дерево. Поэтому, перенабрав код и убедившись, что он работает, приступил к рисованию анимированного дерева. Дальше на помощь приходит d3.js. Там есть замечательные transitions, которые позволяют двигать элементы в нужные позиции и плавно трансформировать в подходящие состояния, по ходу работы алгоритма.

Смысл красно-черных деревьев

Долго думал, как бы по простому, объяснить что к чему. Наверное, все таки надо почитать теорию из разных источников. Как говорится: «Из песни слов не выкинешь». Но простые итоговые выводы в двух словах сформулировать можно. Суть сводится к тому, что есть несколько кейсов при вставке и удалении элемента, в зависимости от которых «дедушки», «папы», «дяди», «дети», «братья» перекрашиваются и сдвигаются (поворачиваются) в сторону, где элементов меньше. В результате никогда не бывает, чтобы путь от самого дальнего узла к корневому был слишком длинным, поэтому поиск нужного элемента в такой структуре происходит очень быстро. Ну а компенсируется это сложностью вставки и удаления.

Источник

Красно-черные деревья: коротко и ясно

Итак, сегодня хочу немного рассказать о красно-черных деревьях. Рассказ будет кратким, без рассмотрения алгоритмов балансировки при вставке/удалении элементов в красно-черных деревьях.

Красно-черные деревья относятся к сбалансированным бинарным деревьям поиска.

Как бинарное дерево, красно-черное обладает свойствами:

1) Оба поддерева являются бинарными деревьями поиска.

2) Для каждого узла с ключом выполняется критерий упорядочения:

ключи всех левых потомков

(в других определениях дубликаты должны располагаться с правой стороны либо вообще отсутствовать).
Это неравенство должно быть истинным для всех потомков узла, а не только его дочерних узлов.

Свойства красно-черных деревьев:

1) Каждый узел окрашен либо в красный, либо в черный цвет (в структуре данных узла появляется дополнительное поле – бит цвета).

2) Корень окрашен в черный цвет.

3) Листья(так называемые NULL-узлы) окрашены в черный цвет.

4) Каждый красный узел должен иметь два черных дочерних узла. Нужно отметить, что у черного узла могут быть черные дочерние узлы. Красные узлы в качестве дочерних могут иметь только черные.

5) Пути от узла к его листьям должны содержать одинаковое количество черных узлов(это черная высота).

Ну и почему такое дерево является сбалансированным?

Действительно, красно-черные деревья не гарантируют строгой сбалансированности (разница высот двух поддеревьев любого узла не должна превышать 1), как в АВЛ-деревьях. Но соблюдение свойств красно-черного дерева позволяет обеспечить выполнение операций вставки, удаления и выборки за время . И сейчас посмотрим, действительно ли это так.

Пусть у нас есть красно-черное дерево. Черная высота равна (black height).

Если путь от корневого узла до листового содержит минимальное количество красных узлов (т.е. ноль), значит этот путь равен .

Если же путь содержит максимальное количество красных узлов ( в соответствии со свойством ), то этот путь будет равен .

То есть, пути из корня к листьям могут различаться не более, чем вдвое (, где h — высота поддерева), этого достаточно, чтобы время выполнения операций в таком дереве было

Как производится вставка?

Вставка в красно-черное дерево начинается со вставки элемента, как в обычном бинарном дереве поиска. Только здесь элементы вставляются в позиции NULL-листьев. Вставленный узел всегда окрашивается в красный цвет. Далее идет процедура проверки сохранения свойств красно-черного дерева .

Свойство 1 не нарушается, поскольку новому узлу сразу присваивается красный цвет.

Свойство 2 нарушается только в том случае, если у нас было пустое дерево и первый вставленный узел (он же корень) окрашен в красный цвет. Здесь достаточно просто перекрасить корень в черный цвет.

Свойство 3 также не нарушается, поскольку при добавлении узла он получает черные листовые NULL-узлы.

В основном встречаются 2 других нарушения:

1) Красный узел имеет красный дочерний узел (нарушено свойство ).

2) Пути в дереве содержат разное количество черных узлов (нарушено свойство ).

Подробнее о балансировке красно-черного дерева при разных случаях (их пять, если включить нарушение свойства ) можно почитать на wiki.

Это вообще где-то используется?

Да! Когда в институте на третьем курсе нам читали «Алгоритмы и структуры данных», я и не могла представить, что красно-черные деревья где-то используются. Помню, как мы не любили тему сбалансированных деревьев. Ох уж эти родственные связи в красно-черных деревьях («дядя», «дедушка», «чёрный брат и крестный красный отец»), прям Санта-Барбара какая-то. Правые и левые, малые и большие повороты АВЛ-деревьев – сплошные американские горки. Вы тоже не любите красно-черные деревья? Значит, просто не умеете их готовить. А кто-то просто взял и приготовил. Так, например, ассоциативные массивы в большинстве библиотек реализованы именно через красно-черные деревья.

Это все, что я хотела рассказать.

Источник